
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула числа размещений без повторений.Содержание книги
Поиск на нашем сайте
Размещения из m по одному. Очевидно, что их число: А Составим размещения по 2: m-строк Итого: А Размещения по 3: В каждой строке будет (m-2) размещений
А 2m -строк Ясно, что А А ……………………………… А Пример: В группе 21 студент. Требуется выбрать старосту, профорга и физорга. Сколькими способами это можно сделать? Решение: Каждая тройка студентов может отличаться от другой тройки или распределением обязанностей, или хотя бы одним из студентов, то есть мы должны вычислить число размещений из 21 по 3: m=21, n=3. А Другой вид формулы числа размещений. Умножим числитель и знаменатель формулы (*) на (m-n)! Получим
А
А Каждое размещение содержит одно и то же количество элементов, взятых из данных m. Перестановки. Размещения из n-элементов по n, каждое из которых отличается друг от друга только порядком элементов, называются перестановками. Их число обозначается
Пример: Сколькими способами могут сесть 6 человек на 6-местную лавочку? Решение: В данном случае каждое расположение лиц на лавочке отличается от другого расположения только порядком. Поэтому мы имеем дело с перестановками:
Сочетания. Сочетания - это размещения, каждое из которых отличается от других хотя бы одним элементом. Другими словами: Сочетания - это соединения, содержащие n элементов из данных m, отличающиеся хотя бы одним элементом. Число сочетаний С С С Пример: В группе 20 студентов. Требуется выбрать 5 делегатов на конференцию. Сколькими способами это можно сделать? Решение: Так как внутри каждой пятерки делегатов перестановки дают одну и ту же пятерку, то каждая пятерка должна отличаться от других хотя бы одним делегатом. В данном случае мы должны посчитать число сочетаний из 20 по 5:
С Свойства сочетаний. 1) С 2) С 3) С 4) С Доказательство: С Что и требовалось доказать. 4) С Доказательство:
Что и требовалось доказать. Размещения с повторениями.
До сих пор мы рассматривали комбинации элементов, которые в каждой комбинации не повторялись. Рассмотрим размещения из m-элементов по n, в которых каждый элемент может повторяться. Такие размещения называются размещениями с повторениями: Ậ Рассмотрим задачу. В лифт 9 этажного дома на 1-ом этаже вошло 10 человек, каждый из которых может выйти на любом этаже, начиная со второго. Сколькими способами они могут выйти из лифта? Решение: Каждый из пассажиров может выйти 8 способами. Два пассажира могут выйти Ậ Таким образом, так как каждый элемент попадает в комбинацию m способами, где n комбинаций, то Ậ
|
||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.195.254 (0.008 с.) |

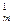 =m
=m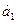
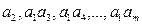 -размещений (m-1)
-размещений (m-1)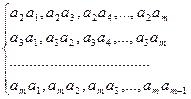
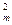 =m(m-1)
=m(m-1)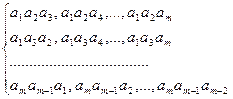
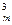 = А
= А 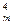 = m(m-1)(m-2)(m-3)
= m(m-1)(m-2)(m-3) = m (m -1)(m -2)….(m -(n -1)) (*)
= m (m -1)(m -2)….(m -(n -1)) (*)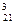 =21*20*19=7980.
=21*20*19=7980.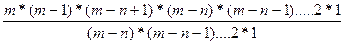 , или
, или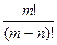
 :
: = n *(n -1)*(n -2)…..2*1, то есть
= n *(n -1)*(n -2)…..2*1, то есть  =6!=720.
=6!=720.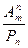 =
= 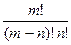
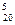 =
= 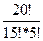 = 15504.
= 15504.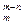 , достаточно выписать формулы левой и правой части равенства.
, достаточно выписать формулы левой и правой части равенства.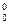 =
= 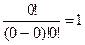 , т.к. по определению 0!=1
, т.к. по определению 0!=1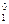 =
= 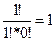 , т.к. по определению 1!=1
, т.к. по определению 1!=1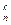 = С
= С 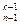 + С
+ С 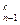
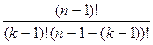 +
+ 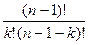 =
= 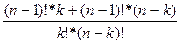 =
= 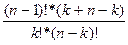 =
= 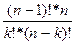 =
= 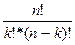 = С
= С  *
* 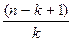
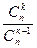 =
= 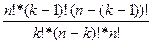 =
= 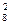 = 8*8=8
= 8*8=8 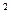 =64. Десять человек могут выйти Ậ 8 10 = 8
=64. Десять человек могут выйти Ậ 8 10 = 8 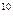 .
. .
.


