
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об оптимальном кодировании.Содержание книги
Поиск на нашем сайте
Пусть имеется распределение вероятностей Р
И пусть имеется префиксная схема оптимального кодирования:
Тогда схема кодирования:
q является префиксной и оптимальной.
Разъяснение: Эта теорема позволяет из оптимального кодирования алфавита, имеющего n-1 букв, составить схему оптимального кодирования для другого алфавита, имеющего n букв, если выполнено условие (5). Смысл теоремы заключается в том, что для распределения вероятностей, состоящих из двух букв, мы можем произвести оптимальное кодирование. Например. Разобьем Далее, продолжая разбивать вероятность р1 = 0,25+0,15, получим новую схему оптимального кодирования Р4 =0,15 11. и т.д. Замечание: Не всякая вероятность может быть разбита на два слагаемых, удовлетворяющих условию (5). Например:
Доказательство теоремы: Схема кодирования (4) – префиксная. Цена кодирования C Схема (6) тоже будет префиксной по построению. Цена кодирования C = = Рассмотрим теперь схему оптимального кодирования
в которой По лемме 2
Так как схема C C Получим C C Что и требовалось доказать. Алгоритм Хаффмена. Пусть имеются распределения вероятностей
Положим
…….
……. (2)
Сложим последние две вероятности Если вероятность первой строки не является суммой, то код первой букве назначен, и мы переходим ко второй вероятности. Разбиваем её и переносим код вниз с приписыванием 0 и 1. И так до тех пор, пока не исчерпаем все суммы. Пример. вероятности 11 12 13 14 15 16 17 18 19 0,25 0,25 0,25 0,25 0,25 0,25 0,290,460,64 0,15 0,15 0,15 0,15 0,220,24 0,25 0,29 0,46 0,12 0,12 0,120,14 0,15 0,22 0,24 025 0,11 0,11 0,12 0,12 0,14 0,15 0,22 0,08 0,11 0,11 0,12 0,12 0,14 0,06 0,08 0,08 0,11 0,11 0,06 0,06 0,06 0,08 0,06 0,06 0,06 0,06 0,06 0,05 В каждом из столбцов подчеркнуты вероятности, являющиеся суммами двух вероятностей. Именно их будем разбивать на соответствующие слагаемые при построении схем оптимального кодирования в соответствии с теоремой об оптимальном кодировании. Перейдем к назначению кодов. Столбец 19 содержит две вероятности, поэтому оптимальными будут коды длиной 1 (столбец 28). Коды 28 27 26 25 24 23 22 21 0 1 00 01 01 01 01 01 1 00 01 10 11 11 11 11 01 10 11 000 001 100 100 11 000 001 100 101 0000 001 100 101 0000 0001 101 0000 0001 0010 0001 0010 0011 0011 1010 1011 В первой строке 19 столбца вероятность подчеркнута. Это значит, что она является суммой. Разбиваем ее на два слагаемых и получаем 18 столбец. Первый код столбца 28 опускаем в две строчки, следующие за последней, и приписываем 0 в одной строке и 1 в другой. Поднимем все строки вверх. Получим коды (столбец 27) для распределения 18 столбца. В первой строке 18 столбца вероятность подчеркнута. Это значит, что она является суммой. Разбиваем ее на два слагаемых и получаем 17 столбец. Первый код столбца 27 опускаем в две строчки, следующие за последней, и приписываем 0 в одной строке и 1 в другой. Поднимем все строки вверх. Получим коды (столбец 26) для распределения 17 столбца. В первой строке 17 столбца вероятность подчеркнута. Это значит, что она является суммой. Разбиваем ее на два слагаемых и получаем 17 столбец. Первый код столбца 26 опускаем в две строчки, следующие за последней, и приписываем 0 в одной строке и 1 в другой. Поднимем все строки вверх. Получим коды (столбец 25) для распределения 16 столбца. В 16 столбце подчеркнута вторая вероятность. Это значит, что она является суммой. Разбиваем ее на два слагаемых и получаем 15 столбец. Первый код столбца 25 уже назначен, поэтому мы его не трогаем, а опускаем второй в две строчки, следующие за последней, и приписываем 0 в одной строке и 1 в другой. Поднимем все строки ниже первой вверх. Получим коды (столбец 24) для распределения 15 столбца. Продолжая в том же духе, получим 21-ый столбец кодов, соответствующих распределению 11 столбца, т.е. исходному распределению.
|
||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.71 (0.01 с.) |

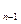 :
: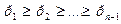 ;
; 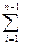
 =1.
=1. ={
={ 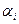
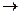
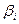 }|
}| 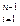 . (4) И пусть существует
. (4) И пусть существует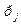 =q
=q 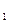 +q
+q 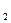 , такое что
, такое что 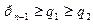 . (5)
. (5)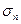 ={
={ 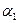
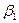 ;…;
;…; 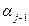
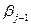 ;
; 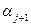
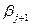 ;…;
;…; 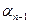
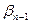 ;
; 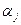
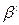 ;
; 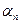
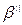 } (6), где
} (6), где 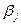 0,
0, 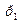 =0,6 - код 0,
=0,6 - код 0, 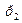 =0,4 - код 1
=0,4 - код 1 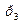 =0,3 01.
=0,3 01.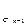 =
= 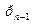
 .
. =
= 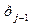
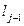 +
+ 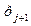
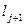 +…+
+…+ 
 +1) + q
+1) + q 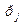 =C
=C 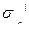 ={
={ 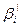 }|
}| 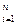 = {
= { 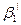 ;…;
;…; 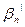 } (7),
} (7),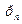 =q
=q 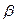 0,
0, 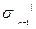 ={
={ 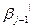 ;
; 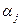
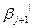 ;…;
;…; 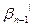 }, следовательно, C
}, следовательно, C 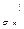 = C
= C 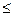 C
C 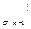 (10).
(10).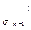 +
+ 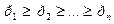 (1),
(1), 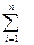
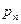 и поместим
и поместим 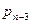
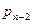
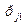 =
= 


