Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о минимальном остовном дереве.⇐ ПредыдущаяСтр 15 из 15
Эта задача довольно часто возникает на практике при строительстве линий электропередач, каналов связи, газопроводов и т.п. Задача. Пусть имеется связный взвешенный граф. Веса можно истолковывать как стоимости, расстояния и т.д. Требуется построить остов с минимальным суммарным весом. (Если граф не связный, то требуется построить минимальный лес). Существует много способов нахождения какого-нибудь остова данного графа. Например, алгоритм поиска в глубину строит остов по ребрам возврата, но этот остов может не быть кратчайшим.
V1 1 V2 V1 1 V2
4 2 2 2 2
V4 1 V3 V4 V3
Рис. 34. Граф. Рис. 35. Дерево кратчайших путей.
V1 1 V2 V1 1 V2
2 2
V4 1 V3 V4 1 V3
Рис. 36. Два кратчайших остова.
Жадный алгоритм Краскала построения кратчайшего остова. Пусть задан связный граф, имеющий р вершин и с различными длинами своих ребер. На первом шаге находим ребро наименьшей длины и помещаем его в будущий остов. Получили подграф. Затем из оставшихся ребер находим второе ребро наименьшей длины и помещаем его в подграф - будущий остов. Затем из оставшихся ребер находим ребро наименьшей длины, не образующее цикла с ранее выбранными ребрами, и помещаем его в подграф. Продолжаем этот процесс до тех пор, пока есть ребра, не образующие цикл в подграфе. Т.к. граф связный, то в подграф попадут все вершины, т.е. подграф будет содержать р вершин. Следовательно, полученный в конечном итоге подграф будет остовным. Т.к. он ацикличен, то он дерево. А т.к. в него включались ребра наименьшей длины, то оно и будет искомым остовом.
Замечание. Поиск наименьшего ребра существенно упрощается, если упорядочить длины ребер по возрастанию. Ориентированные деревья. Орграф называется ориентированным деревом (ордеревом), если 1. существует единственный узел, полустепень захода которого равна 0 (корень), 2. полустепень захода остальных узлов равна 1, 3. все узлы достижимы из корня. Пример.
•
•
Рис. 37. Ордеревья с 4 узлами.
Остальные ордеревья с 4 узлами изоморфны гоафам на рис. 37. Теорема. Свойства оррдеревьев. 1.Если q – число дуг, а p – число узлов оррдерева, то q = p -1. 2. Если в оррдереве отменить ориентацию ребер, то получится свободное дерево. 3. Для каждого узла существует единственный путь из корня. 4. В оррдереве нет контуров. 5. Если в свободном дереве любую вершину назначить корнем, то получится оррдерево. Доказательство. 1. т.к. в каждый узел, кроме вершины, заходит единственная дуга (п. 1,2 определения), то q = p -1 2. Отмена ориентации в оррдереве приведет к созданию связного дерева (иначе нарушается п.3 определения). Из доказанного свойства 1 следует, что этот граф древовиден. Граф связен и древовиден, значит, он – дерево. 3. Если допустить в ордереве наличие контуров, то при отмене ориентации получится граф с циклами, т.е. не дерево, что противоречит свойству 2. 4. Если предположить наличие двух путей для некоторого узла, то при отмене ориентации получится граф с циклами, т.е. не дерево, что противоречит свойству 2.
5. Пусть вершина u назначена корнем. Инцидентные с ней ребра ориентируем в глубину. Т.к. для любой вершины v существует единственная цепь, соединяющая u и v, то полустепень захода d+(v) =1
Упорядоченные деревья. Если в качестве корня в ордереве выбрать какой-нибудь узел v, то множество узлов, достижимых из v образует орграф с корнем v (поддерево). Если относительный порядок поддеревьев установлен, то ордерево называется упорядоченным. Ордеревья и упорядоченные деревья часто используются в программировании. Например, для представления выражений, вложенных блоков, для представления иерархической структуры операторов, структуры вложенности каталогов и файлов, скобочные структуры и т.д. Существует договоренность об изображении корня вверху дерева, направление дуг сверху вниз, что позволяет не рисовать стрелок, если это не приводит к путанице.
Если рассматривать деревья рис. 38 как упорядоченные деревья, то они все различные. Если рассматривать их как ордеревья, то 1 = П, но П ≠ Ш. Если рассматривать их как свободные деревья, то они все изоморфны. Бинарные деревья. В информатике широко используются подмножества множества деревьев, в которых каждый узел является либо листом, либо образует два поддерева – левое и правое. Такой вид деревьев называется бинарным деревом. Бинарное дерево не является упорядоченным ордеревом.
Рис. 38 Пример бинарного дерева.
Бинарное дерево называется полным уровня п, если каждый узел уровня п является листом, а каждый узел меньшего уровня имеет непустые левое и правое поддеревья. Примером полного графа может служить таблица розыгрыша кубка по какому-нибудь виду спорта по олимпийской системе (плей офф). Эйлеровы циклы. Задача о Кёнигсбергских мостах. По Кёнигсбергу протекает река Прегель, образующая два острова, связанных между собой и с берегами семью мостами. Надо разработать такой замкнутый маршрут, в котором каждый из мостов проходится один раз. Эта задача была решена Эйлером в 1736 г.
Рис. 39. Задача о Кёнигсбергских мостах.
Задача сводится к построению циклического графа с 4 вершинами и 7 ребрами так, чтобы каждое ребро входило в него по одному разу. Аналогична задача о рисовании конвертов, не отрывая карандаша и не рисуя дважды одну линию.
Рис.40. Закрытый и открытый конверты
Если граф имеет цепь (цикл), соединяющую две вершины и содержащую все ребра графа по одному разу, то цепь (цикл) называется эйлеровой, а сам граф называется эйлеровым. Теорема. Для того чтобы граф быт эйлеровым, необходимо и достаточно, чтобы число вершин, степень которых нечетна, равнялось 0 или 2. Доказательство: Необходимость: Пусть граф эйлеров, то есть существует или эйлерова цепь, или эйлеров цикл. И пусть имеется одна вершина с нечетной степенью, не являющаяся ни начальной, ни конечной, степень которой равна 2 п +1. Тогда 2 п +1 – е ребро приведет нас в эту вершину п +1-й раз, и покинуть её мы не сможем. Следовательно, такими вершинами могут быть только начальная и конечная. Их две в случае наличия цепи и 0 в случае цикла. Достаточность:
Рис. 41 Начальная и конечная точка цепи
Пусть имеется две вершины с нечетной степенью. Выйдя из вершины А, мы попадем в вершины, из которых всегда можно выйти. Таким образом, все ребра, инцидентные вершинам с четной степенью, будут пройдены, и мы придем к вершине В. Мы можем выйти, затем войти, но опять выйти уже не сможем. Таким образом, между А и В существует эйлерова цепь. Докажем существование эйлерова цикла для вершины А:
Рис. 42 Образование эййлеровоого цикла.
Таким образом, из теоремы Эйлера следует, что задача о Кёнигсбергских мостах и о рисовании закрытого конверта решений не имеют, т.к. вершин нечетной степени больше двух. Задача об открытом конверте решение имеет. Построение его следует начинать из вершины нечетной степени. Гамильтоновы графы. В средине 19 века ирландский математик Уильям Гамильтон опубликовал задачу о «кругосветном путешествии». Требуется обойти все вершины графа (столицы государств) по одному разу и вернуться в исходную вершину.
Рис. 43 Задача о «кругосветном путешествии». Если граф имеет простой цикл, содержащий все вершины графа, то этот цикл называется гамильтоновым циклом, а сам граф называется гамильтоновым графом. Гамильтонов цикл не обязательно содержит все ребра графа. Совершенно очевидно, что гамильтоновы графы являются связными. Решение задачи о «кругосветном путешествии». Находясь в любой вершине, мы можем повернуть вправо (П) или влево (Л). Условимся вместо ПП писать П 2 и т.д. Тогда решение может быть задано формулой (Л3 П3 (ЛП)2)2 = ЛЛЛ ППП ЛП ЛП ЛЛЛ ППП ЛП ЛП. Решение не единственно. Можно начинать в обратном порядке. Можно провести круговую перестановку.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.233 (0.055 с.) |







 • • • •
• • • • • • • •
• • • •


 • • • •
• • • •




 • • • •
• • • •



 • • • • • • •
• • • • • • • • • •
• • • v, и каждый узел достижим из корня.
v, и каждый узел достижим из корня.
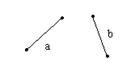 Например, деревья а и b различны.
Например, деревья а и b различны.




















 А В
А В Пусть эйлеров цикл существует для некоторых q
Пусть эйлеров цикл существует для некоторых q  ребер. Докажем, что он существует для q>q
ребер. Докажем, что он существует для q>q 

 ●
●
 ●
● 
 ● ●
● ●



 ● ● ● ● ● ●
● ● ● ● ● ●