
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые общезначимые формулы с кванторами.
1. ( 2. ( 3. ( 4. ( 5. ( 6. ( 7. ( 8. ( 9. ( 10. ( 11. ( 12. ( 13. ( 14. Р (у) Мы ранее установили равносильность левой и правой частей формул 1-8, следовательно, эквиваленциии будут общезначимыми формулами. Идея доказательства формул 9-12 заключается в том, что область истинности левой части включается в область истинности правой части. Рассмотрим на примере формулы 10: ( Будем считать, что предикаты заданы на множестве А. Пусть области истинности предикатов Р (х) и Q(х) не совпадают с А. Тогда левая часть импликации ложна, следовательно, импликация истинна. Если одна из областей истинности совпадает с А, например Мр = А, но тогда ( Докажем теперь формулу 13 - ( Предикат Р задан на некотором множестве U. Пусть Р (у) (у из U) – ложно, но тогда ложно ( Докажем формулу 14: Р (у) Пусть М Рассуждения. Рассуждение- это последовательность высказывательных функций – предикатов, называемых посылками, из которых выводится заключение. Рассуждение считается правильным, если из истинности посылок
Рассмотрим формулу Теорема. Для того чтобы рассуждение (1) было правильным необходимо и достаточно, чтобы формула (2) (импликация конъюнкции посылок и заключения) была общезначимой. Необходимость. Пусть (1) –правильно. Это значит, что посылки истинны и заключение истинно в некоторой области М., но тогда конъюнкция посылок в этой области равна 1, а т.к. заключение истинно, то будет истинна и импликация для всех х из М. значит формула (2) - общезначима.
Достаточность. Пусть формула (2) –общезначима. Это означает, что импликация истинна, по крайней мере, для тех значений переменных, при которых истинна конъюнкция посылок. Значит, для этих значений заключение не может быть ложным, а это означает, это рассуждение правильное. Пример. На множестве рациональных чисел рассмотрим рассуждение: Если число целое, то оно рациональное. Число 3 – целое, следовательно, оно рациональное. Введем обозначения: С (х), х – целое. R(x). х – рациональное. Рассуждение принимает вид ( Рассмотрим формулу В логике высказываний мы имели ряд тождественно истинных формул, названных нами правилами вывода. Подставив в них вместо высказываний предикаты, получим общезначимые формулы, которые тоже назовем правилами вывода. (Названия их см. ранее). другие правила вывода, основанные на общезначимых формулах:
Вывод. Под выводом по-прежнему будем понимать последовательность формул, каждая из которых является посылкой или получена из предыдущих формул по правилу вывода. Последняя формула – заключение. Пример. Если в параллелограмме все стороны равны, то он – ромб. В параллелограмме ABCD все стороны равны, следовательно, он – ромб. Введем обозначения: Р (х), х – параллелограмм с равными сторонами. R(x), x – ромб. Рассуждение выглядит так: ( Построим вывод: 1) ( 2) Р (у) 3) Р(ABCD) – посылка. 4) R (ABCD), ВЕ (2, 3). Можно рассмотреть и другие правила вывода, и другие примеры рассуждений.
Кодирование информации. Задача кодирования. Пусть имеется некоторое множество А = {
Пусть имеется алфавит В= { Задача кодирования заключается в том, что сообщение S, заданное над алфавитом А, преобразуется в сообщение S Общее количество символов Замечание: в качестве буквы алфавита А, могут выступать и сообщения. Функция, обратная функции кодирования F Задача заключается в том, чтобы произвести кодирование, удовлетворяющее некоторым условиям (порой даже взаимоисключающим друг друга). Примеры: Кодирование должно допускать декодирование. Произвести кодирование так, чтобы общая длина кода соответствующая сообщению S, была наименьшей. Кодирование должно быть таким, чтобы при передаче его не было искажения информации. Простота (сложность) декодирования. И т.д. Равномерное кодирование. Равномерное кодирование – это кодирование, при котором каждый элементарный код имеет одинаковую длину. Например, если выбрать в качестве алфавита В цифры, то одноразрядным кодом можно закодировать 10 символов, а двухразрядными числами – 100. Пусть алфавит В содержит к букв, а длина элементарного кода n букв. Сколько символов (m) при равномерном кодировании можно закодировать? Элементарные коды - это кортежи из n букв, взятых из данных к, поэтому они являются размещениями с повторениями. По известной формуле их число равно m = к n (1) Поставим обратную задачу. Имеется m букв алфавита А. Сколько букв должны содержать элементарные коды при равномерном кодировании? Из формулы (1), логарифмируя, получим n = logк m (2) Если же алфавит В={0,1} – двоичный, то закодировать n – битным кодом можно в силу формулы (1) m = 2 n (3) букв. Пусть имеется алфавит А, состоящий из m символов. Сколько бит должен содержать каждый элементарный код при равномерном кодировании? Из формулы (2) получим n = log 2 m (4), если m – степень 2 и по формуле n =\ log где |log Формулы (4) - (5) называются формулами Хартли. Если в качестве алфавита А взять русский алфавит, который содержит 33 символа и пробел, то для 34 символов: по формуле Хартли n =|log Задача: Дано сообщение S. Производится равномерное кодирование длиной k – бит. Найти общую длину кода. Решение: Если длина сообщения |S|= Алфавитное кодирование. Алфавитное кодирование – это кодирование, при котором каждой букве алфавита А соответствует элементарный код алфавита В. Если некоторое слово
|
||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 47; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.16.229 (0.043 с.) |
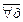 )Р (х)
)Р (х)  (
( х)
х) 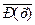 .
.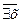 )Р (х)
)Р (х) 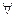 х)
х) 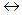 (
( (
(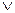 (
(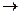 (
(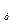 = Ø, тогда (
= Ø, тогда ( Ø, то (
Ø, то (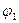 ,
,  ,…,
,…, 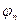 не может следовать ложного заключения.
не может следовать ложного заключения.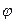 (1)
(1)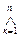
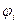
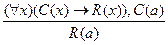 , - ввод единичного (ВЕ).
, - ввод единичного (ВЕ).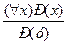 - правило ввода логической функции (ВЛ).
- правило ввода логической функции (ВЛ).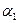 ,
,  ,…,
,…, 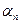 }. Будем называть это множество алфавитом, а объекты – буквами. Кортеж из букв
}. Будем называть это множество алфавитом, а объекты – буквами. Кортеж из букв  =
= 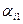 ,
, 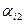 ,…,
,…,  будем называть словом. Последовательность слов – S называется сообщением. Множество сообщений над алфавитом А будем обозначать А
будем называть словом. Последовательность слов – S называется сообщением. Множество сообщений над алфавитом А будем обозначать А 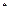 ..
..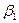 ,
, 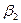 ,…,
,…, 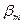 }.
}.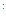 , заданное над алфавитом В (код). Функция f(
, заданное над алфавитом В (код). Функция f( , соответствующая букве алфавита А, называется элементарным кодом этой буквы.
, соответствующая букве алфавита А, называется элементарным кодом этой буквы.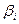 - длина кода.
- длина кода.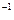 (
(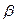 ), называется декодированием.
), называется декодированием.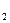 m | + 1 (5),
m | + 1 (5),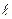 , то длина кода L=k
, то длина кода L=k 


