
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные операции над высказываниями.Содержание книги
Поиск на нашем сайте
Отрицание. Высказывание Таблица истинности:
Пример: р - число 5 делится на 3. р = 0.
Конъюнкция (логическое умножение). Пусть даны два высказывания р и q. Конъюнкцией двух высказываний называется высказывание, которое истинно только тогда, когда истинны оба высказывания. Задается союзом И. Обозначение Таблица истинности:
Пример: А) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 5 - истина.
Б) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 6 - ложь.
3) Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний называется высказывание, которое ложно только тогда, когда оба высказывания ложны. Задается союзом ИЛИ. Обозначение Таблица истинности:
Пример: А) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 5 - истина.
Б) Высказывание р: 15 делится на 4 - ложь. Высказывание q: 15 делится на 6 - ложь.
В) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 6 - ложь.
Импликация. Импликацией двух высказываний р и q называется высказывание, которое ложно только тогда, когда р – истинно, а q- ложно. ЕСЛИ р, ТО q. Обозначение Таблица истинности:
Пример: А) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 5 - истина.
Б) Высказывание р: 15 делится на 3 - истина. Высказывание q: 15 делится на 6 - ложь.
В) Высказывание р: 15 делится на 4 – ложь. Высказывание q: 15 делится на 6 - ложь.
5) Эквиваленция. 6) Эквиваленцией двух высказываний р и q называется высказывание, которое истинно, если оба высказывания принимают одинаковые значения. В словесной формулировке: тогда и только тогда; необходимо и достаточно; если и только если. Обозначение
Таблица истинности:
Пример: р - треугольник равнобедренный. q - углы при основании треугольника равны.
7) Стрелка Пирса - ↓. Логическая операция задается таблицей:
Стрелка Пирса является отрицанием дизъюнкции.
8) Штрих Шеффера - |.
Логическая операция задается таблицей:
Штрих Шеффера является отрицанием конъюнкции. Формулы. Используя определенные выше логические операции (логические связки), мы можем конструировать все более сложные высказывания, которые будем записывать в виде формул. Дадим декларативное определение формулы. 1) 0 и 1 –это формула. 2) Простые высказывания (р) и (q) есть формула. 3) Если ( 4) Других формул нет. Пример: ( Доказательство: (р) и (q)-формулы (по 2), Соглашение о скобках. 1) Элементарные высказывания в скобки заключать не будем. 2) Будем считать, что отрицание связывает сильнее остальных операций, и поэтому скобок писать не будем. 3) 4) 5) Пример: Вместо ((р) Булевы функции. Так как каждое высказывание задается на множестве {0,1}, то любая формула отображает свои значения на множество {0,1}. Таким образом, формула логики высказываний определяет на множестве {0,1} логическую функцию со значениями 0,1. Эти функции получили название булевых. Равносильные формулы. Две формулы Обозначение равносильности: Пример: Φ Их таблицы истинности:
Сравнивая значения столбца Φ Основные равносильности. 1) Коммутативность: 2) р 3) Ассоциативность: 4) (р 5) ( Дистрибутивность: 6) р 7) р Законы Де-Моргана: 8) 9) Поглощение: 10) р 11) р Операции с 0 и 1 12) р 13) р 14) р 15) р Связь с отрицанием 16) р 17) р Связь импликации и эквиваленции с другими операциями 18) 19)
Доказательство этих равносильностей происходит путем построения таблиц истинности.
Используются равносильности при преобразованиях формул. Пример преобразований с использованием равносильностей.:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

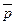 , которое истинно, если р ложно, и ложно, если р истинно, называется отрицанием.
, которое истинно, если р ложно, и ложно, если р истинно, называется отрицанием. .
. .
. .
.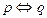
 : Для того чтобы треугольник был равнобедренным необходимо и достаточно, чтобы углы при основании были равными.
: Для того чтобы треугольник был равнобедренным необходимо и достаточно, чтобы углы при основании были равными.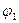 ) и (
) и ( ) - формулы, то (
) - формулы, то ( ) – формула; (
) – формула; ( (
(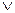 (
(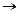 (
( (
(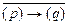 )
)  )-формула.
)-формула. - формула (по 3), (
- формула (по 3), ( Φ
Φ 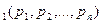 и Φ
и Φ  называются равносильными, если они принимают одинаковые значения при одинаковых наборах значений высказывательных переменных, входящих в эти формулы.
называются равносильными, если они принимают одинаковые значения при одинаковых наборах значений высказывательных переменных, входящих в эти формулы.
 =
= 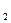 =
= 
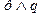
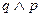 .
.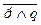
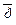
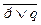
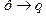
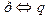
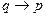 ).
).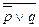
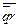

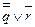

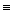 (р
(р 



