Основные законы формальной логики

 

Формальная логика исследует объективно существующие связи между мыслями, которые обусловлены спецификой их логических форм, смыслом входящих в их состав логических терминов. Эти термины выражают как наиболее общие характеристики внеязыковой действительности, так и знание онтологического характера в целом. Примером могут служить такие характеристики, как «невозможно наличие какого-то свойства у предмета и в то же время отсутствие этого свойства у данного предмета» или «у изменяющихся объектов имеются свойства, которые остаются постоянными во многих случаях по крайней мере некоторое время». Эти знания в логике выражаются в виде логически истинных высказываний, то есть высказываний, которые в силу специфики их логических форм являются истинными независимо от того, каковы отличительные особенности входящих в их состав дескриптивных терминов.

Наиболее общие требования, которым должны удовлетворять все рассуждения и логические операции, чтобы быть логически истинными, основные законы формальной логики – это законы тождества, непротиворечивости, исключенного третьего и достаточного основания.

Закон тождества - согласно этому принципу всякое высказывание влечет (имплицирует) само себя, он гласит, что если высказывание истинно, оно истинно. Например, «если сахар сладкий, то он сладкий». Принцип тождества выражает идею, что каждое высказывание является необходимым и достаточным условием своей собственной истинности. Символически он представлен формулой р=р, то есть «р в том и только в том случае, если р». Принцип тождества применим и к именам, в этом случае он принимает вид «Всякое А есть А» и «Некоторые А есть А», где А - это имя, а «некоторые» означает «по меньшей мере или все», но не «только некоторые, но не все». Например, «Всякий круг есть круг», «Некоторые прямоугольники - это прямоугольники».

Закон непротиворечия - принцип, согласно которому высказывание и его отрицание не могут быть одновременно истинными. В этом случае высказывания противоречат друг другу, что является ошибкой. Например, «Солнце встает на востоке» и «Солнце не встает на востоке». Этот принцип подчеркивает, что никакое высказывание не является одновременно истинным и ложным, то есть никакое высказывание не может соответствовать реальному положению дел и одновременно не соответствовать ему. Следствием этого принципа является мысль, что из двух противореча­щих друг другу высказываний одно является ложным, следовательно, допущение противоречия означает введение в свои рассуждения заведомо ложного положения, что недопустимо. Символически принцип непротиворечия выражается формулой Øр&~р – «неверно, что р и не-р», где знакØ означает «неверно, что», & - знак дизъюнкции, а ~ это знак отрицания. Например, «неверно, что дом сделан из кирпича и не сделан из кирпича», «неверно, что аргон – инертный газ и не инертный газ». Необходимо отметить, что речь идет о противоречащих друг другу высказываниях, а не об утверждении о присутствии и отсутствии какого-либо признака в одном высказывании, например, выражение «дом сделан из кирпича и не из кирпича» означает, что при его строительстве использовался не только кирпич, но и бетон, стекло и т.д. Противоречия в языковом контексте иногда является неявным. Так, широко известное утверждение древнегреческого философа Сократа «Я знаю, что ничего не знаю», содержит в себе противоречие. Если Сократ знает, что он ничего не знает, то ему уже что-то известно, пусть это и сведение об отсутствии знаний, либо он не должен знать что ничего не знает.

Закон исключенного третьего - принцип, со­гласно которому истинно или само высказывание, или его отри­цание. Он устанавливает связь между противоречащими друг другу высказываниями, которая заключается в том, что только одно из таких высказываний истинно. Например, «Вторая мировая война началась в 1939 году или она не началась в этом году», «завтра будет футбольный матч или завтра не будет футбольного матча» и т. п. Само название принципа выражает его смысл: дело обстоит так, как описывается в рассматриваемом высказывании, или так, как говорится в его отрицании; третьего варианта нет («третьего не дано»). Символически этот принцип представлен формулой p Ú ~p, где р - некоторое высказывание; Ú - дизъюнкция; ~ - отрицание), «р или не-р». Важно, что высказывания р и не-р нельзя ни принимать, ни отвергать одновременно, так как одно из них обязательно является истинным.

Закон достаточного основания требует, чтобы любое утверждение было обоснованно, то есть истинность суждений должна быть доказана. Основаниями называются суждения, из которых выводится утверждение при его обосновании, следовательно, они должны быть достоверными и их должно быть достаточное количество для того чтобы выводить из них рассматриваемое суждение.

 

                                            

Упражнение 1.

Укажите смысл (собственный или приданный) и значение следующих имен:

1. Человек

2. Академия

3. Холм

4. Гипербола

5. Кентавр

6. Наибольшее натуральное число

7. Самое большое озеро в Северной Америке

8. Водоплавающая птица

9. Автомобиль с разбитой фарой

10. Третий спутник Марса

11. Четвертая от Солнца планета Солнечной системы

12. Кордильеры

 

Упражнение 2.

Определите, какие принципы употребления имен нарушены в следующих контекстах:

1. В институте мы изучаем логику. Мы познакомимся со многими логиками – традиционной и символической, классической и неклассической. После этого для нас не останется тайн ни в логике ребенка, ни в женской логике.

2. Из милицейского протокола: «…на полу лежал труп, рядом сидела жена трупа, а брат трупа лежал в другой комнате без сознания».

3. Помещик Троекуров хотел поймать разбойника Дубровского. Дубровский и француз Дефорж, живший в доме Троекурова – одно лицо. Значит, Троекуров хотел поймать француза Дефоржа, жившего в его доме.

4. Лук – это оружие древних людей. Лук – это растение. Значит, растение – это оружие древних людей.

5. Морковь пишется с мягким знаком. Морковь – это овощ. Значит, овощ пишется с мягким знаком.

6. Материя – это философская категория для обозначения объективной реальности, данной нам в ощущении. Бабушке не хватило материи на фартук. Значит, бабушке не хватило философской категории для обозначения объективной реальности на фартук.

 

Упражнение 3.

Является ли контекст экстенсиональ­ным или интенсиональным:

 

1. Птолемей считал, что Солнце вращается вокруг Земли (относительно терминов «Солнце» и «Птолемей»).

2. Поиск Магелланом пролива из Атлантического океана в Тихий (относительно термина «пролив из Атлантического океана в Тихий»).

3. «Сардиния» - простое единичное имя (относительно термина «Сардиния»)

4. Наш новый сотрудник Петров любит бывать в клубе «Точка» (относительно термин «клуб «Точка»)

Упражнение 4.

Нарушены ли законы формальной логики в следующих рас­суждениях?

1. У офтальмолога. Доктор, раскрывая амбулаторную карту:

- Посмотрим, какие у Вас очки.

Пациент:

 - Поцарапанные, но оправа от Диора.

2. «Гость раскланялся с легкостью неимоверной, сохраняя почтительное положение головы, несколько набок, и в коротких, но определенных словах изъяснил, что он увлекся картинным местоположением его деревни, что несмотря, однако же, на местоположение, он не дерзнул бы обеспокоить его неуместным заездом своим, если б не случилось, по поводу весенних разлитий и дурных дорог, внезапной изломки в экипаже; что при всем том, однако же, если бы даже ничего и не случилось в его бричке, он не мог бы отказать себе в удовольствии засвидетельствовать ему лично свое почтение»[8].

3. С одной стороны, герой книги добивается успеха, так как совершает научное открытие. С другой стороны, герой не добивается успеха, потому что его результаты противоречат традиционной научной школе, и их не оценивают по достоинству.

4. Один философ испытал сильнейшее потрясение, узнав от Бертрана Рассела, что из ложного утверждения следует любое утверждение. Он спросил:

     – Вы всерьез считаете, что из утверждения «два плюс два – пять» следует, что  вы папа Римский?

      Рассел ответил утвердительно.

      – И вы сможете доказать это? – продолжал сомневаться философ.

      – Конечно! – последовал утвердительный ответ, и Рассел тотчас же предложил такое доказательство:

      1) предположим, что 2+2=5;

      2) вычтем из обеих частей по 2: 2=3;

      3) переставим правую и левую части: 3=2;

      4) вычтем из обеих частей по 1: 2=1.

      Папа Римский и я – нас двое. Так как 2=1, то Папа Римский и я – одно лицо. Следовательно, я – Папа Римский».[9]

5. Неверно, что книга является источником знаний, ведь я нашел информацию для доклада только в Интернете. Но неверно, и то, что книга не является источником знаний, ведь все учебники – это книги.

6. Один из ученых пожаловался известному врачу, что он болеет артритом.

  - А ваша мать болела артритом? – спросил врач.

  - Нет.

  - А отец?

  - Тоже не болел.

  - Нет у вас артрита, - заявил врач и, распростившись с пациентом, ушел без дальнейших объяснений.[10]

7. - Надеюсь, я последний раз делаю Вам это замечание.

- Я тоже на это надеюсь.[11]

8. «Ночью один из моих пациентов взял принадлежащее другому каноэ и отправился ловить рыбу при лунном свете. Владелец лодки на рассвете захватил его с поличным и потре­бовал, чтобы тот заплатил ему порядочную сумму за пользо­вание каноэ, а равно и отдал ему весь свой улов. По сущест­вующим у туземцев законам он имел на это право.

С этой тяжбой оба они явились ко мне - и, как то уже случалось не раз и прежде, мне пришлось выступить в роли судьи. Я начал с того, что объявил им, что на моей террито­рии действует не туземный закон, а закон разума, который исповедуют белые и который они услышат из моих уст.

После этого я приступил к дознанию. Я установил, что каждый из них был одновременно и прав, и не прав.         

- Ты прав, - сказал я владельцу каноэ, - потому, что тот человек должен был попросить у тебя разрешения взять твою лодку. Но ты не прав, потому что оказался беспечным и ленивым. Беспечность твоя выразилась в том, что ты про­сто закрутил цепь твоего каноэ вокруг ствола пальмы, вме­сто того, чтобы, как полагалось, запереть на замок. Бес­печностью твоей ты ввел этого человека в соблазн поехать на твоей лодке. А лень твоя привела к тому, что в эту лун­ную ночь ты спал у себя в хижине, вместо того, чтобы вос­пользоваться удобным случаем половить рыбу.

- Ты же, - сказал я, обратясь к другому, - виноват в том, что взял лодку, не спросив позволения ее владельца. Но ты одновременно и прав - в том, что оказался не столь ленив, как он, и не захотел упустить лунной ночи, не вос­пользовавшись ею для рыбной ловли.

После этого в соответствии с существующим обычаем я по­становил, что ловивший рыбу должен отдать одну треть своего улова за пользование лодкой владельцу последней, вторую же треть может оставить себе, ибо затратил силы на ловлю рыбы.

Оставшуюся треть я постановил передать в пользу больницы, по­тому что дело происходило на ее территории и самому мне пришлосьзатратить время на разрешение их палавры»[12] (Schweitzer А. Afrikanische Geschichten.).[13]

                                Глава 3. ПОНЯТИЕ

Учение о понятии

 

Понятие – важнейший вид мыслей, так как в нем отражаются сущностные характеристики действительности в процессе абстрактного мышления. Логика исследует понятия как мысли особого виды, способы выявления логических форм понятий, установления отношений между понятиями.

Понятие – это мысль, в которой обобщены в класс и выделены из некоторого множества предметы согласно их существенным признакам, общим только для этих предметов. В данном случае слово «предмет» употребляется в широком смысле, представляя как материальные, так и духовные объекты.

Существенным является признак, неотделимый от качественных характеристик объекта, необходимый для того, чтобы выделить этот объект из совокупности различных объектов. Признак является положительным, если он утверждает наличие какого-либо свойства, состояния предмета либо отношения его к другим объектам: например, «болеть ветрянкой», «Быть севернее Рима». Признак является отрицательным, если он утверждает отсутствие какого-либо свойства, состояния предмета либо отношения его к другим объектам. Например, «не любить сладкого», «не быть столицей Италии».

Различают также необходимые и случайные признаки. Необходимым является признак, при отсутствии которого объект теряет свое качество, перестает быть самим собой. Так, например, необходимым признаком материи является признак «быть объективной реальностью, данной нам в ощущении», воздействовать на чувственные познавательные способности человека, в отличие от такого феномена, как общественное сознание, которое также является объективной реальностью, не будучи материей. Случайным является признак, при отсутствии которого объект своего качества не теряет, остается самим собой. Например, случайным признаком кружки будет «изготовленная из фаянса», так как кружки могут изготавливаться также из металла, пластмассы и пр.

Языковой формой выражения понятий являются общие описательные имена. Неописательные имена выражают понятия только в том случае, когда они введены в качестве сокращений для общих описательных имен, то есть в том случае, если они имеют приданный смысл, являющийся понятием, и этот смысл известен. В случае, если это требование не соблюдается, может произойти подмена понятия именем, не выражающим его.

Понятие характеризуется с точки зрения своего объема и содержания.

Содержание понятия – это множество признаков, исходя из которых предметы обобщаются и выделяются в понятие. Под признаком имеется в виду наличие или отсутствие у предмета некоторого свойства, а также наличие или отсутствие отношения между предметами. Предметы, обобщаемые в понятии, выделяются из некоторого множества предметов – это множество называется универсумом рассуждения или родом понятия.

В логике выделяются логическое и фактическое содержание понятия. Логическое содержание – это информация, представленная логической формой понятия, которую изучают, отвлекаясь от смыслов и значений входящих в состав понятия терминов. Зная логическое содержание понятия, можно установить является ли оно универсальным, то есть представлен ли в нем весь универсум рассуждения, а также является ли оно пустым, то есть имеется ли в наличии ситуация, когда в понятии не выделяется ни один предмет из универсума рассуждения.

Фактическое содержание понятия – это информация о предметах, обобщаемых в понятии. Различают основное фактическое содержание и полное фактическое содержание понятия. Основное фактическое содержание – это система только тех признаков, на основе которых предметы обобщались и выделялись в понятие. В этом случае вся остальная информация об этих предметах, их свойствах, отношениях с другими предметами не учитывается. Полное фактическое содержание учитывает все знание об объекте, включая и те признаки, по которым осуществлялось обобщение в понятие.

Объем понятия – это совокупность предметов, называемых понятием, то есть множество предметов, таких, для которых характерно наличие признаков, образующих содержание понятия. Как и в случае с содержанием, в логике выделяются логический и фактический объемы понятия. Логический объем – это совокупность предметов, которым принадлежат признаки, представленные  логической формой понятия. Фактический объем – это множество предметов, обладающих признаками, в которых содержится информация о существенных характеристиках, на основе которых эти предметы выделяются в особый класс.

Объем понятия состоит из элементов, отдельных  объектов, характеризующихся существенными для этого понятия признаками. Так, например, элементами объема понятия «автомобиль» являются отдельные разнообразные автомобили. В свою очередь, части объема понятия – это подклассы объема понятия, которые не совпадают с ним и не являются пустым множеством, например, частями объема понятия «автомобиль» являются легковые автомобили, грузовые автомобили и т.д.

Графически объем понятия обычно представляют в виде круга, каждая точка которого представляет какой-то элемент объема понятия. Например, объем понятия «автомобиль» можно представить в виде круга А:

А

                                   

                                               

 

Объемы и содержания понятий находятся в тесной взаимозависимости. Одно из важнейших проявлений этой связи фиксируется в законе обратного отношения между содержаниями и объемами понятий. Он звучит так: в случае, когда имеются два понятия с одинаковым универсумом (родом) и содержание первого понятия меньше содержания второго, то объем первого понятия больше, чем объем второго. Иными словами, если одно понятие беднее другого по содержанию,  то первое шире второго по объему; если же первое понятие богаче второго по содержанию, то оно уже его по объему.

Отношение «быть уже (шире) по объему» между понятиями есть не что иное, как строгое включение одного класса в другой класс: понятие хА(х) уже понятия  хВ(х) по объему, если и только если каждый элемент объема понятия хА(х) содержится в объеме понятия хВ(х), но некоторые элементы объема второго понятия хВ(х) не содержатся в объеме первого понятия хА(х). Понятие хА(х) богаче понятия хВ(х) по содержанию, если и только если из информации о том, что произвольный объект из универсума этих понятий обладает признаком а можно с использованием знаний о взаимосвязях, имеющихся в данной предметной области, извлечь информацию о том, что он обладает также признаком в, но из информации о наличии признака в у объекта нельзя извлечь информацию о том, что он обладает признаком а.

Закон обратного отношения действует как для фактических, так и для логических объемов и содержаний.

Упражнение 1.

Дайте характеристику признаков.

1. Быть хорошим спортсменом.

2. Не быть краеведческим музеем.

3. Быть шофером, но не быть таксистом

4. Не делиться на 15.

5. Бежать со скоростью 10 км/ч

6. Любить классическую музыку.

7. Иметь плотно закрывающуюся крышку.

8. Относиться к классу живых существ, способному к коммуникации.

­

Упражнение 2.

Сравните содержания и объемы следую­щих понятий.

1. Число, которое делится без остатка на 5 и на 10. Число, которое делится без остатка на 10.

2.  Млекопитающее. Куница.

3. Человек, знающий все европейские языки. Человек, знающий все восточноевропейские языки.

4. Живое существо, способное к коммуникации посредством речи. Живое существо, способное к коммуникации.

5. Министр. Министр иностранных дел.

6. Человек, являющийся  учащимся, но не являющийся школьником. Человек, являющийся учащимся.

7. Ребенок, родившийся в городе. Ребенок, родившийся в столице государства.

8. Студент, сдавший хотя бы один экзамен. Студент, сдавший экзамен по логике.

9. Человек, читающий в метро. Человек, читающий газету.

Упражнение 3.

Укажите фактические и логические объе­мы и содержания следующих понятий.

1. Город России с населением более миллиона человек.

2. Самый большой город Германии.

3. Разумное существо, обладающее членораздельной речью.

4. Наука о мышлении.

5. Наука об обществе.

6. Мост через Берингов пролив.

7. Мышь, умеющая говорить по-французски.

 

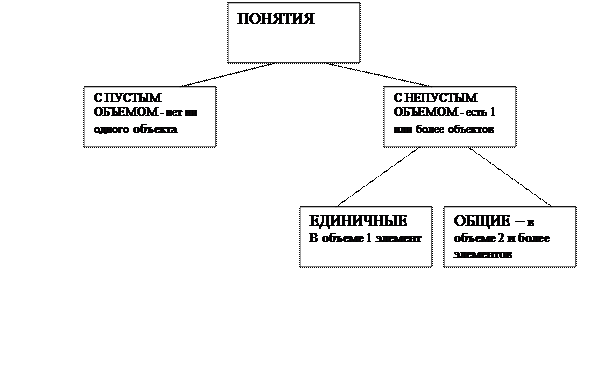
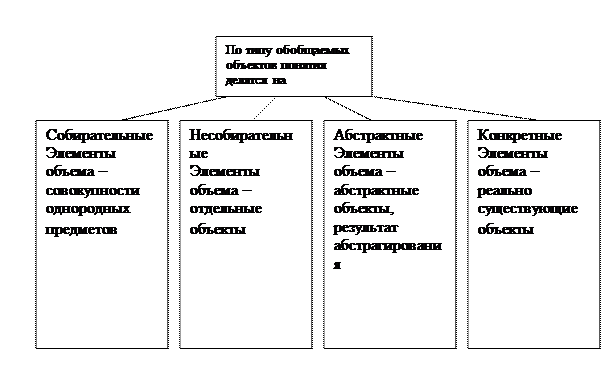
                           §2. Виды понятий и отношения между ними

А) Виды понятий

Понятия, используемые в науке и во всех других областях человеческой деятельности, чрезвычайно многообразны по своей структуре, типам обобщаемых в них объектов и другим характеристикам. Типологизация понятий, то есть выделение и систематизация их различных видов может проводиться по разным основаниям - их делят на виды, во-первых, исходя из особенностей содержаний, и, во-вторых, учитывая специфику их объемов и элементов объемов.

По количеству обобщаемых предметов понятия делятся на понятия с пустым объемом и понятия с непустым объемом. Пустым по объему является понятие, в объеме которого нет ни одного предмета, в то время как содержанием таких понятий являются признаки, не принадлежащие ни одному предмету из его универсума. Например, «человек, который является вегетарианцем, но ест мясо» или «студент, который не сдал ни одного экзамена, но сдал экзамен по истории».

В первом случае понятие имеет пустой фактический объем, так как противоречиво фактическое содержание понятия, в рамках имеющегося знания нам должно быть известно, что вегетарианцы не едят мяса. Логический объем в данном случае пустым не является. Во втором случае пустым является и логический объем, так как содержание противоречиво не только фактически, но и логически, одновременно представлены и утверждение, и его отрицание, что, согласно принципу исключенного третьего, невозможно.

Понятия, логические содержания которых непротиворечивы, а фактические противоречивы, чаще всего возникают вследствие недостаточности наших знаний об исследуемом предмете. В науке формулируются понятия не только об известных объектах, но и о тех, существование которых лишь предполагается, и если в результате развития научного знания выяснится, что это предположение было ошибочно и в действительности таким понятиям ничего не соответствует, неоспоримо, что их фактическое содержание противоречиво. К числу таких понятий относятся, например, «флогистон», «мировой эфир», «эоантроп»[14].

Кроме того, в целях построения теорий, в науке формулируют понятия, фактическое содержание которых является противоречивым, ибо известно, что формулируемые признаки противоречат реальному положению дел, например, «абсолютно твердое тело», «точка» или «идеальный газ». Подобные понятия являются результатом процесса идеализации, мыслительного конструирования понятий об объектах, явлениях и процессах, не существующих в действительности, но таких, для которых имеются прообразы в реальном мире – в данном случае отвлекаются от признаков, несущественных для цели исследования и абсолютизируют признаки, существенные для этой цели. Идеализация позволяет формулировать законы, строить абстрактные схемы реальных процессов, используется в моделировании.

Понятия с непустым объемом подразделяются на единичные и общие. Единичные понятия – те, в объеме которых содержится только один элемент, общие понятия – те, в объеме которых содержится два и более элементов.

Исходя из характеристики  обобщаемых предметов понятия делятся, во-первых, на собирательные и несобирательные, во-вторых, на абстрактные и конкретные. Собирательными являются понятия, элементы объемов которых представляют собой совокупности однородных предметов, мыслимых исключительно как целое, например, «стадо», «группа студентов», «коллектив ученых». Перечисленные понятия являются общими. Единичными являются такие собирательные понятия, объем которых состоит только из одного элемента, например, «российский народ», «группа НТБ-301 Московской финансово-промышленной академии в 2007-2008 учебном году».

Несобирательными являются понятия,  объема которых состоит из отдельных объектов. Например, «студент», «ученый», «Московская финансово-промышленная академия».

Абстрактными называются понятия, объем которых состоит из абстрактных объектов, представляющих собой результат абстрагирования, например, «совесть», «трудолюбие», «чернота».

Понятия, в которых обобщаются реально существующие предметы, обладающие определенными признаками, называются конкретными, например, «трудолюбивый ученик», «черный плащ».

Исходя из особенностей признаков, на основе которых выделяются и обобщаются предметы, составляющие содержание понятия, понятия делятся, во-первых, на положительные и отрицательные, во-вторых, на относительные и безотносительные.

В положительном понятии утверждается наличие какого-либо признака, а в отрицательном наличие признака отрицается. Так, если положительными понятиями являются такие, как «злой человек», «говорящий по-немецки», «стоящий в очереди», то отрицательными, в свою очередь, будут понятия «незлой человек», «не говорящий по-немецки, «не стоящий в очереди». 

Относительными являются понятия, содержанием которых является наличие некоторого отношения выделяемых в понятии предметов к другим предметам, иными словами, эти предметы существуют только в отношении к определенным предметам. Например, понятия «дед» - не имея внуков, нельзя стать дедом; «вдова» - не имея мужа, который скончался, нельзя стать вдовой; «заместитель директора» - невозможно быть ничьим заместителем, необходимо наличие некоторого вышестоящего лица, которое можно замещать.

В свою очередь, безотносительными являются понятия, которые выделяют предметы, существующие сами по себе, на основе наличия или отсутствия у них их собственных характеристик, например, «цветок», «вода», «медведь».

 

 

 

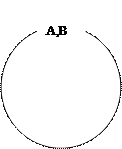
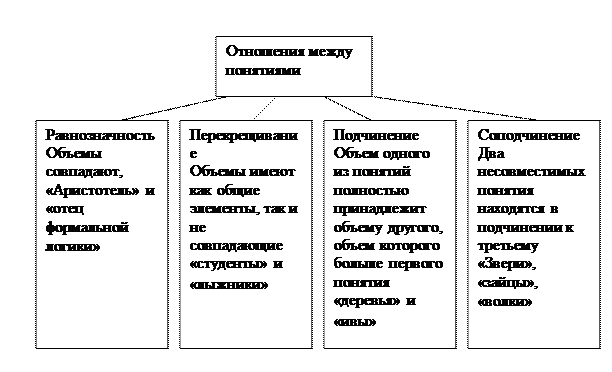
      Б) Отношения между понятиями

Предметы, как реально существующие, так и вымышленные, обладают разнообразными признаками, и сходными, и различными между собой. Соответственно, между любыми понятиями, их обозначающими, объективно существуют некоторые отношения, исходя из их логических характеристик, содержания и объема. На основе их изучения логика разработала строгую систему отношений между понятиями.

По характеру отношений между объемами понятия делятся на совместимые и несовместимые. Совместимыми являются понятия, объемы которых имеют общие элементы, могут полностью либо частично совпадать. Так, совместимыми являются понятия «студент» и «учащийся», «студент» и «человек, умеющий играть на гитаре». Несовместимыми являются понятия, объемы которых не имеют общих элементов, например, такие, как «человек» и «автомобиль», или «раб» и «рабовладелец».

Совместимые понятия могут находиться в отношениях: 1) равнозначности, 2) перекрещивания, 3) подчинения, 4) соподчинения.

Понятия, объемы которых совпадают, являются равнозначными. Примером такого отношения являются понятия «Аристотель» и «основоположник формальной логики». Графически отношение равнозначности представляется следующим образом: объем первого понятия показан кругом А, объем второго – кругом В

 

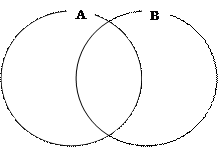
Понятия, объем одного из которых частью входит в объем второго, а объем второго частью входит в объем первого, находятся в отношении перекрещивания. Например, перекрещивающимися являются понятия «школьник» и «человек, умеющий играть на пианино». В данном случае общими элементами будут школьники, умеющие играть на пианино. Графически это отношение изображается в виде кругов А и В

 

 

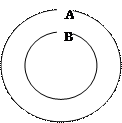
Понятия, объем одного из которых полностью принадлежит объему второго, то время как объем второго больше объема первого понятия, находятся в отношении подчинения. Например, понятия «студент музыкального училища имени Гнесиных» (В) и «студент» (А), графически отношение между которыми представляется в виде схемы

 

 

 

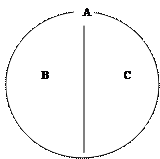
Отношение соподчинения возникает, когда два несовместимых понятия находятся в подчинении к третьему, то есть эти два понятия не имеют общих элементов объемов и одновременно находятся в состоянии подчинения к одному и тому же понятию. Например, понятия «медведь» (В) и «лошадь» (С) находятся в отношении соподчинения к понятию «млекопитающее» (А). Данное отношение графически выражается в виде

Если же два понятия, находящиеся в отношении соподчинения, исчерпывают собой объем третьего понятия, например, в случае «основные классы рабовладельческой общественно-экономической формации» (А), «рабовладельцы» (В), «рабы» (С), то графическая схема будет иметь вид 

Чтобы установить отношения между несколькими понятиями, их также изображают в виде круговых схем, а потом попарно называют отношения между понятиями.

 

 

Упражнение 1.

Охарактеризуйте вид каждого из сле­дующих понятий:

1. Неопределенность.

2.Сосед

3. Человек, не умеющий играть в шахматы.

4.Невыносимая легкость бытия.

5. Первый космонавт, долетевший до Юпитера.

6. Вице-президент корпорации

7. Не имеющий квартиры в собственности

8. Налоговая декларация.

9. Некоторые из тех, кто бодрствовал после того, как все уснули.

10.Сверхразумное существо, живущее на Марсе.

11. Рекламный щит

 12. Нескоростной транспорт

13. Не пришедшая на занятия группа студентов

14. Светлая тьма.

15. Сознание.

16. Не бывший в употреблении товар

17. Скорость движения

18. Движение

                                                                                      

 

Упражнение 2.

Назовите отношения между понятиями и изобразите их посредством круговых схем:

1. Дом, строение

2. Липа, береза, дерево

3. Останкинская башня, телебашня в Москве

4. Школьники, филателисты

5. Канцелярские принадлежности, скрепки, карандаши

6. Курящие люди, некурящие люди

7. Основатель МГУ и М.В.Ломоносов, обучавшийся в Славяно-Греко-Латинской Академии

8. Эмоции, злость, радость

9. Химия, физика, естественные науки

10. Орудие преступления, огнестрельное оружие

 

        Упражнение 3.

        Установите, в каких отношениях попар­но находятся следующие понятия, изо­бразите отношения между их объемами посредством круговых схем.

1. «Преступление», «мошенничество», «грабеж»

2. «Человек, изучивший все европейские языки», «человек, изучивший итальянский язык», «человек, не изучивший некоторых европейских языков».

3. «Треугольник», «прямоyгoльный треугольник»; «непрямоугольный треугольник».

4. «Художник»;. «импрессионист»; «французский художник».

5. «Друзья»; «партнеры»; «коллеги».

6. «Монархическое государство», «средневековое государство», «государство»

ОПЕРАЦИИ С ОБЪЕМАМИ ПОНЯТИЯ

А) Булевы операции с объемами понятия

 

Подобно тому, как в математике проводятся различные операции над числами, такие, как сложение, вычитание, умножение, деление, возведение в степень и т.д., в логике также были сформулированы основные принципы проведения операций над объемами понятий, то есть классами. Поскольку объемы понятий суть множества, над ними можно осуществлять те же операции, что и над множествами.  Они названы булевыми в честь английского логика Дж.Буля, который построил особую алгебру логики. В числе этих операций пересечение классов, объединение классов, дополнение к классу, вычитание классов.           

Допустим, даны два понятия хА(х) и хВ(х), таких, что объем первого понятия есть WxA (x), объем второго понятия  есть WxB (x). Тогда операции с объемами понятия будут иметь следующий вид.

Пересеченuе двух объемов понятий. Это операция, в результате применения которой к объемам понятий WxA(x) и WxB(x) образуется класс WхА(х) ∩ WxB(x), элементами кото­рого являются те и  только  те  предметы,  которые  одновременно входят  как в класс WxA (х), так и в класс WxB(х). Эта операция обозначается знаком ∩.

Графически класс WхА(х) ∩ WxB(x) выделяется при помощи заштрихованных поверхностей. Могут быть следующие случаи пересечения объемов понятий:

 

Объединение двух объемов понятий. Это операция, в результате применения которой к объемам понятий WxA(x) и WxB(x) образуется класс WхА(х) È  WxB(x), элементами кото­рого являются те и  только  те  предметы, которые одновременно входят по крайней мере в один из объемов этих понятий. Она обозначается знаком «È».

На схемах класс WхА(х) È  WxB(x) выделен заштрихованными поверхностями:

 

 

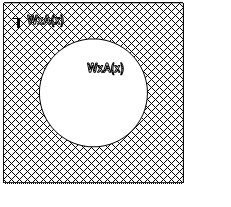
         Дополнение к объему понятия (взятие дополнения) – это операция, в результате применения которой к объему понятий WxA(x) образуется класс ┐ WхА(х), элементами кото­рого являются те и  только  те  предметы из области значений переменной х, которые одновременно не входят в класс WxA(x).

Графически эта операция представлена в виде, где класс ┐ WхА(х) обозначен заштрихованной поверхностью:

Вычитание понятий – это операция, в результате применения которой к объемам понятий WxA(x) и WxB(x) образуется класс WхА(х) \  WxB(x), элементами кото­рого являются те и  только  те  элементы класса WхА(х), которые одновременно не являются элементами класса WxB(x). Она обозначается знаком «\».

 На схемах класс WхА(х) \ WxB(x) выделен заштрихованными поверхностями:

 

Особенность применения к объемам понятий булевых операций - объединения, пересечения, разности множеств, взятия дополнения к множеству - состоит в том, что в результате получается множество, которое является объемом нового, сложного понятия, образуемого из содержаний исходных. Так, дополнением к объему понятия является объем отрицательного понятия. Объединение объемов понятий дает объем разделительного понятия, пересечение их объемов - объем соединительного понятия, результатом теоретико-множественного вычитания второго объема из первого будет объем соединительного понятия.

Б) Обобщение и ограничение понятий

Кроме булевых операций к понятиям применяются также операции обобщения и ограничения, в основании которых лежат родо-видовые отношения. В случае, когда имеются два непустых понятия хА(х) и хВ(х), понятие хА(х) является родовым, а понятие хВ(х) видовым, если и только если понятие хВ(х) находится в отношении подчинения к понятию хА(х). Это отношение обозначается символом «Ì».

Например, из двух понятий «студент» и «студент второго курса» первое является родовым, а второе видовым, объем первого понятия больше, чем объем второго и, соответственно закону обратного отношения, содержание родового понятия является частью содержания видового понятия.

Обобщением понятия называется переход от непустого понятия с данным объемом к непустому понятию с более широким о