Правила, используемые в аргументативных процессах.

                             ГЛАВА 1. ПРЕДМЕТ ЛОГИКИ.

 

         § 1. Основные этапы становления логики

 

Название науки логики происходит от древнегреческого слова «λογος», которое означает «разум», «рассуждение». 

Логика является одной из древнейших наук на Земле. Она возникает как часть риторики, науки об ораторском искусстве, в связи с необходимостью построить правильную, убедительную, последовательную речь. Другой областью, где логика была широко распространена, была практика судопроизводства. В использовании логики нуждались также возникающие в эпоху античности естественные науки, в первую очередь, математика.

Одним из первых исследований в области логики была формулировка логического закона тождества в учении элейского философа Парменида. В своем произведении «О природе» он формулирует понятие единой неделимой материи, которая всегда остается равной себе и постоянно находится в одном и том же состоянии. Философами элейской школы разрабатывается учение об аргументации. Для того, чтобы доказать некие положения, они формулируют последовательность дедуктивных умозаключений.

Известный древнегреческий философ Гераклит разрабатывает учение о противоречии. По его мысли сущее находится в постоянном изменении, основой которого является единство противоположностей, одной из которых является единство бытия и небытия.

Демокрит, основоположник учения об атомистическом строении материи, считается творцом первой системы логики в Древней Греции. Им был написан трактат «О логике», или «Канон», в трех книгах. Демокрит заложил основы учения о модальностях, понятиях необходимости, возможности и случайности.

Новый этап древнегреческой философии связан с философской школой софистов. Они впервые ставят в центр философского исследования проблему человека, его жизни в обществе и государстве. Будучи представителями релятивизма в философии, они утверждали, что не существует абсолютной истины, которую разделяли бы все люди, а потому каждый имеет право на отстаивание собственной истины в споре. Риторика и искусство спора получают весьма важное развитие в школе софистов, особенно значительный вклад в риторику был внесен Протагором, Горгием и Тразимахом. Софисты в первую очередь изучают логику с точки зрения техники дискуссии, как средство для отстаивания своей      позиции. Так, Протагором был написан труд «Искусство спорить». Следуя идее о том, что в любом вопросе существуют противоположные мнения, он развивает теорию диалога, участники которого отстаивают противоречащие друг другу позиции. Протагор строит рассуждение таким образом: необходимо выяснять позицию собеседника, задавая ему вопросы и показывая ошибочность его ответов. Он также изучает различные способы выведения умозаключения для того чтобы использовать их как логические приемы в ораторской речи.

Один из известнейших древнегреческих философов, Сократ, особое внимание уделяет формулированию метода рассуждения для достижения истинного знания. При этом он использует два логических приема: индукцию и дефиницию (определение). Индукция, процесс рассуждения от единичных вещей к формулированию общего понятия, является основой определения. В процессе образования понятия необходимо выяснить, какие характеристики являются существенными для вещи, а какие – несущественными. Существенные характеристики выражают природу вещи, то, чем в действительности она является.

Логические воззрения Сократа находят свое развитие в творчестве Платона, родоначальника систематического объективного идеализма. В диалоге «Теэтет» устами своего учителя Сократа он критикует определение как простое перечисление объектов, обладающих общими свойствами. Сократ спрашивает: «Что такое знание?» В ответ ему начинают перечислять, какие виды знания бывают, тогда он объясняет, что подобное перечисление может не иметь предела вследствие многообразия различных областей знания. Приведение примеров недостаточно для дефиниции, в определении следует объяснять сущность предметов.

Сущностью вещей является то общее, что принадлежит всем вещам, присущим одному роду. Важно, однако, отметить, что знание об общем в вещах приходит не в эмпирическом опыте – по Платону, истинное знание есть припоминание того, что душа человека видела до его рождения, находясь в мире первичного бытия - мире идей. Процесс образования понятия – «синагогэ» - состоит в сведении знания о множественных вещах к единому понятию. Этот процесс неотделим от «диайрезиса», деления по родам, которое Платон использует не в целях классификации, но для того, чтобы осуществлять дефиницию, определение понятия – в этом случае будет понятно, какие характеристики вещи не являются важными. «Различать все по родам, не принимать один и тот же вид за иной или иной за тот же самый… Кто в состоянии выполнить это, тот сумеет в достаточной степени различить одну идею, повсюду пронизывающую многое, где каждое отделено от другого; далее он различает, как многие отличные друг от друга идеи охватываются извне одною и, наоборот, одна идея связана в одном месте совокупностью многих, наконец, как многие идеи совершенно отделены друг от друга. Все это называется уметь различать по родам, насколько каждое может взаимодействовать (с другим) и насколько нет»[1].

Платон формулирует правила деления, сохраняющие свое значение и поныне: во-первых, деление должно производиться по действительно существенным различиям предметов, во-вторых, в процессе деления нельзя пропускать промежуточных ступеней.

Платон также вносит вклад в развитие теории суждения. Суждение устанавливает отношение между терминами, которые могут быть отношениями тождества, равенства, различия и т.д.; эти отношения необходимы и универсальны независимо от того, каковы соединяемые ими термины. Суждения могут быть двух видов: эмпирические, полученные в опыте, и чистые, разумные. Формулировать эмпирические суждения можно лишь на основе разумных суждений. Так, в упомянутом выше диалоге «Теэтет» Платон приводит пример, что основой эмпирического суждения о равенстве в предметах чувственно воспринимаемого мира является разумное суждение о равенстве вообще.

Важнейшая роль в развитии логики Древней Греции принадлежит Аристотелю  (384 до н.э. – 322 до н.э.). Именно он сформулировал и систематизировал важнейшие положения формальной логики, многие из которых остались незыблемыми и по сей день. Отмечая роль греческого мыслителя в развитии логики, один из первых российских исследователей этой науки, Е.А.Бобров, писал: «Основным фондом и субстратом всех наших дальнейших логических реформ, ее постоянной основой…является логика Аристотеля… цельный и жизнеспособный тип логики»[2]. Логические сочинения Аристотеля были объединены под общим названием «Органон».

Главной целью аристотелевской логики было исследование бытия и истины; логическое учение этого мыслителя было тесно связано с его метафизикой. Слово, взятое само по себе, по мнению Аристотеля, не заключает в себе ни истину, ни ложь, является нейтральным. Истинными и ложными могут быть только суждения и умозаключения, как утверждает философ, истина и ложь получаются только при соединении, когда нечто о предмете утверждается, и разъединении (когда нечто отрицается) отдельных элементов мысли. Так, например, само по себе слово «трегелаф», обозначающее вымышленное существо, являющееся наполовину оленем, наполовину козлом, не истинно и не ложно, ложным будет суждение «трегелаф существует», а истинным – «трегелаф не существует».

Аристотель обращает особое внимание на вопрос, что является критерием истинности. Он выделяет два таких критерия – материальный и формальный. Материальный критерий означает, что наши размышления соответствуют реальному положению дел в окружающем нас мире. Истину, по Аристотелю, высказывает тот, кто соединяет свои элементы мысли о вещах таким образом, как эти вещи соединены во внешнем мире. Суждения соединяются при помощи силлогизма и индукции; при совершении этих логических операций также должно соблюдаться соответствие с действительностью, что может легко быть проверено с помощью опыта.

Формальный критерий истины означает соответствие принципов нашего мышления общим законам. Аристотель выделяет три таких закона: противоречия, исключенного третьего и тождества. Основным законом он считает закон противоречия, поскольку этот закон отвергает случаи, когда нечто и существует, и не существует.

Суждению в логике Аристотеля уделяется большое внимание. Он осуществляет классификацию суждений по трем основаниям: по качеству (утвердительные и отрицательные суждения), количеству (общие, частные, единичные суждения) и модальности (возможные, действительные и необходимые).

Аристотель формулирует различие таких отношений между суждениями, как контрарность (противная противоположность) и контрадикторность (противоречащая противоположность). Он устанавливает те положения, которые впоследствии были названы логическим квадратом: общеутвердительные и общеотрицательные суждения находятся в отношении контрарной противоположности, а общеутвердительные и частноотрицательные, а также общеотрицательные и частноутвердительные (попарно) суждения находятся в отношении контрадикторной противоположности. Он также развивает учение об обращении суждений.

Учение о понятии занимает в логике Аристотеля не столь важное место, так как он исследует его в своей метафизике. Тем не менее следует отметить, что мыслитель установил соотношение между понятиями и категориями, сформулировал учение об иерархии понятий внутри категорий, изучал отношение между понятиями по их объему, утверждая, что говорить о степени общности между понятиями можно лишь в том случае, когда эти понятия принадлежат к одной и той же категории.

Огромное значение для развития логики имело учение Аристотеля о силлогизме вообще и о категорическом силлогизме, в частности. Он сформулировал понятие силлогизма как дедуктивного умозаключения, в котором из данных суждений необходимо вытекает новое суждение. Строго доказательным, по Аристотелю, является только категорический силлогизм, который он называет силлогизмом через средний термин. В свою очередь, совершенный категорический силлогизм – это силлогизм первой фигуры, в котором логическая необходимость выводов очевидна.

Важную роль в познании Аристотель отводит и индукции, считая ее более наглядным, по сравнению с дедукцией, методом, однако строго научной признает только полную индукцию, которой даже дает название силлогизма по индукции, отмечая ее доказательность. По словам Е.А.Боброва, Аристотель «доказывает, что различие между силлогизмом и индукцией заключается только в положении среднего термина, а именно, обыкновенный силлогизм состоит в связывании двух крайних терминов посредством среднего, не входящего в заключение. В индукции же, по Аристотелю, с помощью одного из крайних терминов связывается средний термин с другим крайним, то есть термин, который в соответствующем силлогизме был бы средним, входит уже в индукции в состав вывода»[3].

 Разновидностью индукции у него являются умозаключения по аналогии, которые он называет парадейгмами. Эти умозаключения имеют особую форму. Мысль движется не от общего к частному, как в случае дедукции, и не от частного к общему, как в случае индукции, а от частного к частному, при условии, что они соответствуют одному термину. Таково, например рассуждение: «Война фиванцев с фокейцами есть зло. Война фиванцев с фокейцами есть война с соседями. Война с соседями есть зло. Война афинян с фиванцами есть война с соседями. Значит, война афинян с фиванцами есть зло».

Аристотель изучает также энтимему, которая, на его взгляд, представляет собой силлогизм «из вероятного», в котором пропущена одна из посылок, хотя она и подразумевается.

В эпоху Древнего Рима появление оригинальных идей в логике обнаруживается в первую очередь в философском творчестве стоиков и эпикурейцев. Стоикам принадлежит мысль о том, что логическая доказуемость является важным признаком истинного знания. Соответственно, учение о доказательстве является центральной частью стоической логики. Доказательство состоит из умозаключений, элементами которых являются суждения. Только суждения, в которых нечто утверждается о предмете, можно оценивать с точки зрения их истинности или ложности, степени соответствия реальному положению дел. Умозаключения должны оцениваться как правильные либо неправильные исходя из их логической формы. Для того чтобы заключение в целом было истинным, необходимо выполнение двух условий. Во-первых, посылки должны быть истинными суждениями, во-вторых, чтобы вывод заключения из посылок был правильным по форме.

Серьезное внимание стоики уделяют проблеме знака – объекта, обозначающего некую вещь. Они приходят к выводу, что между знаком и вещью, которую он обозначает, существует необходимая связь. Например, когда утверждается, что «дым есть знак огня» или что «шрам свидетельствует о ране», совершенно необходимо, что в отсутствие огня отсутствует и дым, а в случае, когда человек не был ранен, у него не появится шрам. Поскольку этот вывод невозможно сделать в момент единичного непосредственного ощущения, необходимо соотнесение множества фактов, постольку знание о связи между знаком и вещью является умопостигаемым.

Эпикур и его последователи были представителями материалистического направления в философии. Рассматривая вопрос об истинности знания, они уделяли большое внимание практическому познанию, полученному на основе эмпирических данных при помощи индукции и аналогии. Эпикурейцы приходят к выводу, что для того чтобы индукция и аналогия были достоверными, необходимо соблюдать определенные требования. Наблюдения, в ходе которых получают опытные данные – основу индукции и аналогии – должны быть как можно более точными, исследовать повторяющееся множество случаев. При изучении этих опытных данных следует выделять наиболее важные, существенные свойства и только на их основе делать общие выводы при помощи индукции. В случае аналогии и этого недостаточно, ибо, когда мы мыслим о наличии свойств у предмета на основе его сходства с другими предметами, обладающими этими свойствами, достоверное знание может быть получено, если такие предметы принадлежат к родственным классам.

Эпикур также изучает гипотезу как важное средство развития знания. Он считает, что при выдвижении гипотез необходимо соблюдать следующие правила: при объяснении проблемы рассуждения в гипотезе не должны содержать апелляции к сверхъестественным силам, а также не должны противоречить имеющимся доказанным фактам.

Однако наиболее распространенными в древнеримской логике были работы, комментировавшие известнейшие труды Аристотеля. Среди мыслителей, посвятивших свое творчество аристотелевской логике, выделяются неоплатоники Порфирий (232 – ок.305 гг.) и Боэций (480-524 гг.), чьи труды стали основой средневековой западноевропейской логики вплоть до XIII столетия.

Новый этап в развитии европейской логики связан с появлением сочинения Петра Испанского (1220—1277)[4] «Малая сумма логики» (“Summulae logicalis”), которое представляло собой систематизацию и синтез логической средневековой мысли. Этой книгой в Европе пользовались почти три столетия, уже после изобретения книгопечатания она издавалась множество раз и была основным учебником по логике. «Малая сумма логики» состоит из семи трактатов, первые шесть из которых излагают содержание аристотелевского «Органона» в виде определений и правил, снабженных мнемоническими средствами. Они посвящены рассмотрению предложений, универсалий (категорий), предикаментов, силлогизмов, топики, а также ошибок и ложных умозаключений. Седьмой трактат, называемых «О свойствах терминов», заключал в себе подведение итогов того нового, что было внесено в логику в течение предыдущего двенадцатого столетия. Особый интерес в нем представляет учение о суппозиции, подстановке одних терминов в предложениях вместо других. Это происходит в случаях, когда вместо термина, который принадлежит объему понятия, подставляется термин, представляющий само это понятие, например, в предложении «Кай смертен» термин Кай (один из людей по имени Кай) можно заменить термином «человек»: «человек смертен». Петр Испанский излагает также сведения о возможных расширениях и ограничениях терминов в предложениях, о правилах именования, правилах распределения терминов при присоединении к ним различных кванторов.

Известным мыслителем в области средневековой логики был Раймунд Луллий (около 1235 - около 1315). Ему принадлежит положение об особом методе или искусстве, посредством которого можно с разумной необходимостью вывести из общих понятий различные истины. Следуя учению реализма, философской концепции, представители которой считали что универсалии, общие понятия, существуют наряду с обозначаемыми ими вещами, Луллий считал, что реальность есть не что иное, как правильное и постепенное усложнение общих понятий через их различные комбинации друг с другом.  Вследствие этого связь вещей может быть открыта путем следования разума за логическим порядком универсалий. Используя символические обозначения общих понятий, Луллий моделировал логические операции при помощи различных логических схем и машин, наиболее известным из которых было «логическое колесо», идея которого сформулирована в труде «Великое искусство» (“Ars magna”). Оно состояло из нескольких кругов, независимо друг от друга вращавшихся на одной оси. Круги были разделены на «камеры», разделы, где в определенном порядке были написаны слова и буквы, обозначавшие философские и богословские понятия. Разделы занимали определенное положение относительно разделов других кругов. Произвольно вращая круги, можно было получить множество комбинаций, в которых Луллий усматривал новые истинные умозаключения. Изобретение «логического колеса» фактически было предвестием комбинаторных методов в логике.

Фрэнсис Бэкон (1561-1626), один из наиболее известных представителей эмпиризма Нового времени, автор учения о том, что единственным источником знания является опыт, выступил против силлогистики Аристотеля как главного метода получения истины и провозгласил основным научным методом, при помощи которого может быть достигнуто истинное знание, индукцию. Бэкон критикует аристотелевское учение об индукции, называя его индукцией через простое перечисление, и формулирует индуктивный метод, важная роль в котором принадлежит операции исключения. Этот метод состоит из трех таблиц: а) таблицы присутствия (в ней перечисляются все известные случаи, где встречается исследуемое явление); б) таблицы отсутствия (в ней приводятся случаи похожие, где, однако, исследуемое явление отсутствует);  в) таблицы степеней (в ней перечисляются случаи, где исследуемое явление представлено с большей или меньшей интенсивностью). Следующий этап – индукция через исключение, отказ от случаев, где исследуемое явление не представлено.

Таким образом, получая опытным путем максимально возможное количество фактов, относящихся к изучаемому явлению, мы должны выделить несущественные условия этого явления и исключить их, чтобы в результате остались лишь условия существенные.

На основе материала, представленного в этих таблицах, отыскивается, какое свойство всегда сосуществует с исследуемым свойством и всегда отсутствует, когда отсутствует исследуемое свойство, а также вместе с последним увеличивается и уменьшается.

Рене Декарт (1596—1650), представитель рационалистического направления в философии Нового времени, которое постулировало разум как единственный источник знания, также придавал большое значение роли научного метода для достижения истины. По его мнению, образцом подлинно научного метода является математика. Декарт формулирует свои мысли следующим образом: «Я, вместо того большого числа правил, из каких слагается логика, думал – довольно мне четырех следующих правил, только я бы решился твердо и постоянно соблюдать их без отступления…

Первое: принимать за истинное лишь то, что с очевидностью познается мною таковым, то есть избегать поспешности и предубеждения и принимать к суждению лишь то, что представляется так ясно и раздельно моему уму, что никаким образом не может быть подвергнуто сомнению.

Во-вторых, дробить каждую из трудностей, какие буду разбирать, на столько частей, сколько только можно, дабы их лучше разрешить.

В-третьих: всякие мысли по порядку начинать с предметов простейших и мельчайших, и восходить мало-помалу как по ступеням до познания более сложных…

В-последних, делать всюду перечни столь полные и обзоры столь общие, чтобы быть уверенным, что ничего не упущено»[5]. Главным критерием истинности для Декарта является ясность и отчетливость наших мыслей. Он выделяет такие методы достижения истины, как интуиция, дедукция, индукция, сравнение и аналогия, причем особо подчеркивает значение дедукции.

На основе философского учения Декарта его последователи П.Николь и А.Арно в 1662 году опубликовали труд под названием «Логика, или Искусство мыслить»[6]. В нем авторы излагают учение о понятиях, их классификации; о сложных терминах; уделяют значительное внимание умозаключениям, силлогизмам, энтимемам. Целью логики, по их мнению, является задача служить инструментом для других наук. Ими высказывается мнение о том, что необходимо выработать новый язык науки, свободный от неясности и неопределенности терминов; разрабатывается понимание суждения, в частности, особо подчеркивается познавательное значение выделяющих суждений (вида «только некоторые S суть P») и исключающих суждений (вида «все S, кроме одного, суть P»).

Продолжателем дедуктивной линии Декарта был известный философ Г.В.Лейбниц (1646-1716). Ему принадлежит дальнейшая разработка логических законов мышления, в частности, большинство специалистов в области истории логики считают, что Лейбниц сформулировал закон достаточного основания. Этот закон постулирует, что ни одно утверждение не может быть истинным и справедливым, ни одно явление не может быть истинным или действительным без достаточного основания, почему дело обстоит так, а не иначе. Лейбниц формулирует его, исходя из признания универсальной взаимосвязи и всеобщей причинности в мире.

Наиболее важным логическим законом Лейбниц считал закон тождества, формулируя его таким образом: «Всякая вещь есть то, что она есть».

Особое внимание Лейбниц уделяет проблеме модальностей и понятию вероятности как объективно зависящей от природы самих вещей большей или меньшей возможности того или иного явления.

Лейбниц выдвинул идею о том, что возможно создание логики как универсальной математики, сформулировал положения о применении математической символики в логике и построении логических исчислений. Ему принадлежит мысль о создании универсального языка рассуждений, в котором силлогистика будет лишь частным случаем. Некоторые идеи, выдвинутые им в работе «Об искусстве комбинаторики», написанной в 1666 году, предвосхитили положения современной математической логики.

Следующий этап в развитии традиционной логики связан с именем английского философа Джона Стюарта Милля (1806 – 1873). В сочинении «Система логики силлогистической и индуктивной» он утверждает, что источником знаний являются опыт и наблюдение, а единственно научный метод – это индукция. Милль развивает теорию индукции, систематизировав и обобщив достижения предшествовавших английских логиков Дж.Гершеля и У.Уэвелля. Он формулирует и иллюстрирует многочисленными примерами пять методов научной индукции: 1) метод единственного сходства, 2) метод единственного различия, 3) соединенный метод сходства и различия, 4) метод отсутствующих изменений, 5) метод остатков.

Математическая (символическая) логика как совершенно новое, отличное от традиционной формальной логики направление в науке возникает лишь в девятнадцатом столетии. Это направление в логике представляет высказывания на основе формализованных языков, основными элементами которых являются специальные символы, которые определенным образом интерпретируются. Возникновение математической логики связывают в первую очередь с именами британских ученых Дж.Буля и У.Джевонса, чьи идеи послужили основанием для исследований в этой области.

Джордж Буль (1815 – 1864) отличает от обычного языка язык символический, используемый в точных науках, исследует исчисление классов и высказываний. Буль выделяет в логике четыре основные операции: сложение (в исчислении классов сложению классов соответствует их объединение с исключением общей для них части, в исчислении высказываний – строгая дизъюнкция), умножение (в исчислении классов умножению соответствует пересечение классов, в исчислении высказываний - конъюнкция), дополнение Х до единицы (в исчислении классов эта операция означает дополнение к классу Х, в исчислении высказываний – отрицание Х), вычитание (это операция, обратная к операции сложения). Основное отношение в логике Буля – отношение равенства.

У.Джевонс (1835-1882) исследовал эффективные способы решения логических задач и теорию исчисления классов. Ему принадлежит идея о том, что научная индукция – это применение обратного метода математической теории вероятностей. Стремясь применить разработки логики и математики на практике, Джевонс создал логическую машину, принцип работы которой был основан на аналогии между логической операцией исключения несовместимых с посылками комбинаций классов и механическими движениями ее рычагов.

В дальнейшем теория исчисления классов развивалась Э.Шредером (1841-1902), который совершенствовал методику Дж. Буля для приведения логических выражений к нормальным формам; Дж. Венном (1834 – 1923), изучавшим теорию классов и создавшим особый графический аппарат диаграмм, при помощи которого выражаются математические, теоретико-множественные или логические отношения между множествами; Г.Фреге (1848-1925), который осуществил аксиоматическую трактовку исчисления высказываний, заложил основы математической теории доказательства и логической семантики, исследовал смысл и значение имен. В 1910-1913 годах публикуются три тома «Principia mathematica» Б.Рассела и А.Уайтхеда, первый труд в области символической логики, где были сведены воедино ее достижения.

В настоящее ученые развивают различные отрасли и направления неклассической логики. Среди них, такие, как многозначная логика, модальная логика, логика норм и т.д. Современная логика имеет множество приложений, среди них такие, как теория доказательства, теория множеств, логика вероятностей, индуктивная логика и т.д.

 

 

Предмет логики

 

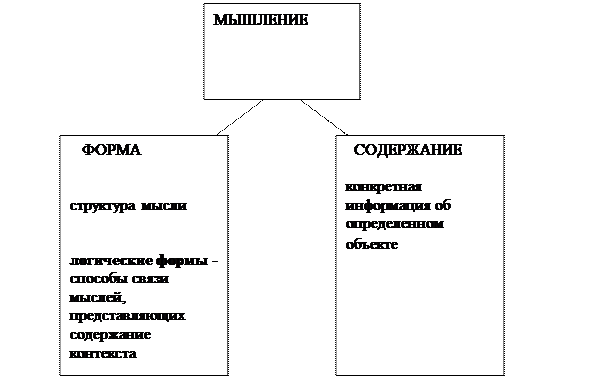
 Необходимо отметить, что в настоящее время слово «логика» используется в нескольких основных значениях. Это и объективная логика закономерностей в развитии и изменении явлений и предметов объективного окружающего нас мира, и субъективная логика законов человеческого мышления. Логика как наука изучает эту вторую область, исследуя как наиболее общие характеристики реальных предметов и явлений, так и свойства отражающих их мыслей и отношений между ними.

В мышлении выделяют форму и содержание. Содержание – это конкретная информация об определенном объекте, форма – структура мысли, раскрывающей эту информацию. Изучая языковой контекст, логика делает предметом своего рассмотрения логические формы - способы связи мыслей, представляющих содержание этого контекста. Для того чтобы выявить логические формы мыслей, необходимо отвлечься от значений и смысла входящих в состав высказываний нелогических дескриптивных терминов, терминов, обозначающих какой-либо предмет, свойство или отношение[7], подставив на их место символы-переменные А, В, S, P, M и т.п. Каждый из символов-переменных соответствует определенному термину.

Например, в случае рассуждения «Все млекопитающие - позвоночные животные. Ни один комар не является позвоночным животным, значит, ни один комар не является  млекопитающим» при замене переменными нелогических терминов рассуждение будет иметь вид: Все P суть М. Ни один S не суть М. Следовательно, ни один S не суть P.

 Несмотря на то, что при установлении логической формы отвлекаются от смысла содержательных терминов, она несет в себе информацию, касающуюся этих терминов. В данном случае это информация о том, что если все предметы класса Р включены в класс М и ни один предмет класса S не включен в класс М, то ни один предмет класса S не включается также и в класс Р.

Необходимо отметить, что между мыслями существуют связи, которые зависят только от их логических форм. Такие связи между мыслями по форме, что истинность одной из мыслей обусловливает истинность другой, называются формально-логическими законами. В приведенном выше примере вместо символов-переменных S, P, M можно подставить любые нелогические термины таким образом, чтобы высказывания, в состав которых они включены, были истинными по смыслу, и в любом случае при истинности исходных высказываний получаемое высказывание будет истинным. Подобная связь между мыслями представляет собой логический закон. Законы логики – это нормы, в соответствии с которыми должны осуществляться рассуждения, в противном случае наши выводы могут быть неверными.

Чтобы установить, является ли логическим законом некоторое рассуждение, необходимо произвести исследование, возможна ли такая ситуация, что при подставлении вместо символов-переменных произвольных терминов того же типа, что и эти переменные, окажется, что полученное высказывание не будет истинным при условии истинности исходных высказываний (такая ситуация называется контрпримером). Если эта ситуация невозможна, значит, связь между исходными высказываниями – это логический закон, если она возможна, значит, этой связи нет и рассуждение является неправильным.

Например, имеется рассуждение: Студенты – люди. Следовательно, умный студент является умным человеком. Его логическая форма: «Все S суть Р. Следовательно, все Sn суть Рn». Для него можно найти контрпример – «Мыши – животные. Следовательно, крупные мыши – крупные животные», высказывание, которое не является истинным, значит, оно не является логическим законом.

Необходимо учесть, что требование к рассуждению - иметь правильную логическую форму - является необходимым, но недостаточным условием развития научного знания. Правильный по логической форме вывод может быть ложным по своему содержанию, если посылки были ложными и содержание вывода не соответствует положению дел в действительности.

 

Логика и мышление

 

Будучи нормативной наукой, регулирующей интеллектуальную познавательную деятельность людей, логика включает в себя изучение важнейших элементов рационального познания.

Процесс познания осуществляется как движение от незнания к знанию, от знания поверхностного, не­полного к знанию глубокому и полному и представляет собой единство двух ступеней: чувственного познания и рационального познания, или абстрактного мышления.

В чувственном познании выделяют три формы: ощущение, восприя­тие и представление.

Начальной формой познания является ощущение. Ощущение ­- это отражение объектов посредством органов чувств. Оно возникает и существует в процессе непосредственного контакта с объектом и дает знание об отдельных сторонах этого объекта. Восприятие представляет собой чувственно конкретный, целостный образ вещей или явлений действительности и также возникает в процессе взаимодействия субъекта и объекта. Представление, как и восприятие, имеет наглядный чувственно-конкретный характер, но оно является воспроизведением в сознании человека целостного образа объекта, воздействовавшего на его органы чувств в прошлом. Будучи вследствие этого менее четким, чем восприятие, представление становится основой для обобщения, выделения повторяющегося в предметах, абстрагирования.

Чувственное познание, тем самым, это основа рационального познания, абстракт­ного мышления, которое представляет собой процесс оперирования образами. Формами рационального познания выступают понятие, сужде­ние, умозаключение, гипотеза и теория.

  Понятие - это мысль, отражающая в обобщающей форме существенные признаки предметов и явлений действительнос­ти.  Его формирование – результат сложных операций абстрагирования, анализа, синтеза данных чувственного опыта.

Суждение - это мысль, в которой что-нибудь утверждается об объекте, ему приписывается наличие или отсутствие некоторых свойств. Например: дождь не идет, роза красная, ученик читает.

Мыслительная связь нескольких истин­ных суждений и выведение из нее определенного итога в форме нового суждения о предметах, явлениях, процессах называется умозаключе­нием. Иными словами, умозаключение - логическая форма получения знания, заключающаяся в движении мысли от определен­ных исходных данных к новому знанию, складывающемуся на основе этих данных.

Гипотеза представляет собой такое знание, истинность или лож­ность которого еще предстоит установить. Она формулируется в поисках выхода из проблемной ситуации, которые появляются в связи с развитием науки либо с осознанием ограниченности знаний. Научная гипотеза должна соответствовать принципам научного подхода к объяснению действительности, учи­тывать ранее установленные наукой факты и законы, обладать способностью к практической экспериментальной проверке. Оправданность гипотезы прямо пропорциональна тому, насколько увеличивается число согласующихся с ней фактов в ходе ее проверки.

 Результатом познавательной деятельности является теория, особая форма научного знания, в которой содержится обобщенное представление о существенных связях и закономерностях некоторой области действительности, выступающей в качестве объек­та данной теории.

Значение логики

 

 Логика присутствует повсюду, как на макроуровне общественной жизни, научных исследований, экономики и производства, так и на микроуровне жизни отдельного человека.

Логическая культура мышления - то есть способность результативно использовать логические приемы и способы рассуждения - очень важна. Человек не только способен точно и грамотно выражать свои мысли, но и делать верные выводы; убедительно обосновывать свои размышления, делать их понятными для других; доказать свою точку зрения, объяснив ошибочность рассуждений оппонента; зная правила и законы логики, можно быстро найти ошибку в рассуждениях оппонента. Объясняя, почему способ рассуждения является верным или нет, логика предоставляет возможность анализировать и незнакомые способы рассуждения. Поэтому важно не только знание правил и законов логики, но умение применять эти законы и правила на практике.

Любая наука строится по законам логики. Логика – неотъемлемая часть философии, юридической науки, педагогики, языкознания и т.д. В современных условиях, когда наблюдается активное усложнение системы знаний и коммуникации, логика способствует оптимизации процессов выработки, хранения и передачи информации; она используется при создании и эксплуатации разнообразной электронно-вычислительной техники, в компьютеризации производства.

         

Упражнение 1.

Выявите логические формы следующих утверждений:

1.Все млекопитающие являются позвоночными.

2. Некоторые грибы являются съедобными.

3. Ни одна звезда не является обитаемой.

4. Некоторые студенты являются спортсменами.

5. Если некоторые люди являются талантливыми, то неверно, что ни один человек не является талантливым.

6. Неверно, что все лекарства являются невкусными.

7. Вс