
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование функции комплексного переменного.
Пусть в каждой точке некоторой гладкой кривой Разобьем кривую Интеграл существует, если Обозначим
Полученная формула показывает, что вычисление интеграла от функции комплексного переменного сводится к вычислению двух криволинейных интегралов от действительных функций действительных переменных. Свойства интеграла в комплексной области аналогичны свойствам криволинейного интеграла. Пример. Вычислить Решение. По условию
Рис.6 Разобьем контур интегрирования на две части 1)
2)
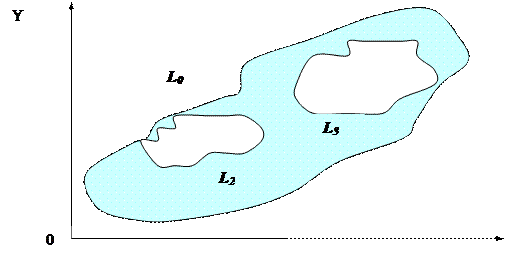
3) Теорема Коши для односвязной области. Если функция Доказательство. Мы показали, что Следствие. Если функция Теорема Коши для многосвязной области. Если функция
Рис.7 Следствие. Для аналитической функции в многосвязной области интеграл по внешнему контуру равен сумме интегралов по внутренним контурам при условии, что интегралы по внешнему и внутренним контурам берутся в одном направлении.
Для аналитической в замкнутой области функции Интегралы от элементарных функций комплексного переменного в области их аналитичности вычисляются с помощью тех же формул и методов, что и в действительном анализе. Например, Интегральная формула Коши. Если функция Эта формула позволяет вычислить некоторые интегралы, к которым не применима теорема Коши. Пример.Вычислить по формуле Коши Решение. а) Точка б) Точка
Литература: /1, глава II §1-5 / или /2, глава IIIV § 28,29/ или /3, глава 1 § 2,5/.
Вопросы для самопроверки. 1. Дайте определение области на комплексной плоскости. Какая точка называется граничной? Как определяется граница области? 2. Дайте определение степенной функции на комплексной плоскости. 3. Как определяется показательная функция на комплексной плоскости? Сохраняются ли ее свойства? Какое новое свойство она приобретает? Выведите формулу Эйлера. Запишите комплексное число в показательной форме. 4. Как определяются тригонометрические функции 5. Дайте определение логарифмической функции на комплексной плоскости. 6. Сформулируйте определения предела и непрерывности функции комплексного переменного в точке. 7. Дайте определение производной функции комплексного переменного. Какая функция называется аналитической? Выведите необходимые и достаточные условия аналитичности функции. 8. Как определяется интеграл от функции комплексного переменного? 9. Сформулируйте теоремы Коши для односвязной и многосвязной области и следствия из них. 10. Как применяется формула Коши для вычисления некоторых интегралов? 2.8. Задачи для самостоятельного решения. 1) Вычислить интеграл 2) Вычислить интеграл 3) Вычислить интеграл 4) Вычислить по формуле Коши: а) б) г)
2.9. Особые точки. Определение. Точки, в которых нарушается аналитичность функции, называются особыми. Точка Отметим, что это определение справедливо только для односвязной области. Различают три типа изолированных особых точек. 1) Точка 2) Полюсом порядка К называется такая изолированная особая точка 3) Точка Пример 1.
Пример 2. Пример 3. Задачи для самостоятельного решения. Установить вид особых точек для следующих функций: 1) Вычеты. Понятие вычета является одним из важнейших понятий теории функций комплексного переменного. Если функция Определение. Вычетом функции
Обозначается вычет:
Теорема 1. Вычет функции Доказательство. Пусть точкой. Доопределим функцию
Теорема 2. Если функция Доказательство. По определению простого полюса
Пример. Найти вычет функции Решение. Заданная точка является простым полюсом. Поэтому
Теорема 3. Если функция Например, для полюса второго порядка эта формула принимает вид: Для полюса третьего порядка Пример. Найти вычет функции
Решение.
Найдем производную второго порядка данной функции.
С учетом этого результата получим:
Теорема 5. Основная теорема о вычетах. (Коши, 1825г.). Если функция Доказательство. По теореме Коши для многосвязной области
Пример.Вычислить Решение. Подынтегральная функция имеет две особые точки: 1)
2) 3) 2.11. Задачи для самостоятельного решения. 1) Определить вычеты функции относительно ее особых точек: а) г) 2) С помощью вычетов вычислить интегралы: а) б) в) г) д) е)
|
|||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.166.7 (0.07 с.) |
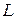 с началом в точке
с началом в точке 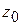 и концом в точке
и концом в точке 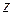 определена непрерывная функция
определена непрерывная функция 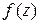 .
.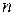 частей (элементарных дуг) в направлении от
частей (элементарных дуг) в направлении от 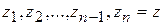 . На каждой элементарной дуге
. На каждой элементарной дуге  выберем произвольную точку
выберем произвольную точку 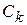 и составим интегральную сумму
и составим интегральную сумму 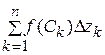 , где
, где  . Предел такой интегральной суммы при стремлении к нулю длины наибольшей из элементарных дуг, если он существует, называется интегралом от функции
. Предел такой интегральной суммы при стремлении к нулю длины наибольшей из элементарных дуг, если он существует, называется интегралом от функции  .
.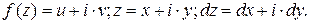 Подставим эти выражения под знак интеграла. Получим
Подставим эти выражения под знак интеграла. Получим 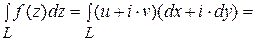
 .
. , если
, если 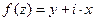 , контур
, контур  с вершинами в точках
с вершинами в точках 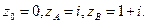
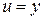 ,
, 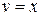 . Искомый интеграл принимает вид:
. Искомый интеграл принимает вид: 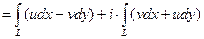
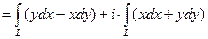 .
.
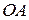 . и
. и 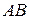 . Вычислим интеграл по этим контурам.
. Вычислим интеграл по этим контурам.
 .
. 
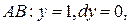
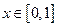 .
.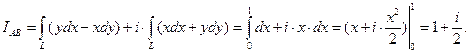

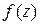 является аналитической в односвязной области и ее производная непрерывна, то для всех кривых
является аналитической в односвязной области и ее производная непрерывна, то для всех кривых 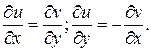 Из математического анализа известно, что условиями независимости криволинейного интеграла
Из математического анализа известно, что условиями независимости криволинейного интеграла 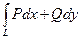 от контура интегрирования является равенство:
от контура интегрирования является равенство:  Справедливость этого равенства подтверждается условиями Эйлера – Даламбера, т.е. криволинейные интегралы
Справедливость этого равенства подтверждается условиями Эйлера – Даламбера, т.е. криволинейные интегралы  и
и 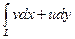 не зависят от контура интегрирования, а зависят только от начальной и конечной точек.
не зависят от контура интегрирования, а зависят только от начальной и конечной точек. .
.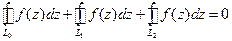
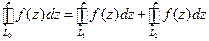 .
. . Если зафиксировать точку
. Если зафиксировать точку 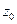 , а точку
, а точку  менять, то указанный интеграл будет функцией от
менять, то указанный интеграл будет функцией от 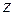 :
:  . Можно доказать, что для аналитической в замкнутой области функции
. Можно доказать, что для аналитической в замкнутой области функции 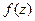 функция
функция 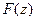 также является аналитической, причем
также является аналитической, причем 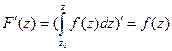 . Функция
. Функция  . Легко показать, что справедлива и формула Ньютона-Лейбница:
. Легко показать, что справедлива и формула Ньютона-Лейбница:  .
. .
.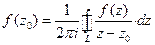 , где контур обходится так, что область остается слева.
, где контур обходится так, что область остается слева.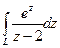 , если
, если 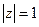 , б)
, б) 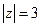 .
.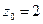 , в которой подынтегральная функция не является аналитической, лежит вне круга
, в которой подынтегральная функция не является аналитической, лежит вне круга 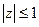 . Поэтому по следствию из теоремы Коши для односвязной области интеграл по любому замкнутому контуру равен нулю.
. Поэтому по следствию из теоремы Коши для односвязной области интеграл по любому замкнутому контуру равен нулю.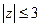 .
. По формуле Коши имеем:
По формуле Коши имеем:
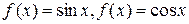 на комплексной плоскости?
на комплексной плоскости?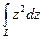 , если контур
, если контур 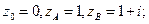 б) отрезок, соединяющий точки
б) отрезок, соединяющий точки 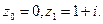
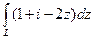 , если контур
, если контур 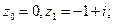 б) часть параболы
б) часть параболы  , соединяющей эти точки.
, соединяющей эти точки. , если контур
, если контур 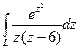 , если
, если 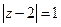 , б)
, б) 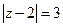 ,
,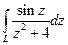 , если
, если 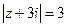 , в)
, в)  , если
, если  ,
,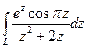 , если
, если 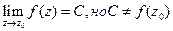 .
. . Если
. Если 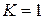 , полюс называется простым.
, полюс называется простым. функция
функция 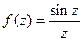 . Точка
. Точка 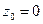 является устранимой особой точкой, т.к.
является устранимой особой точкой, т.к. .
. 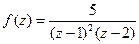 . Точка
. Точка 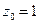 является полюсом второго порядка, а точка
является полюсом второго порядка, а точка  . Точка
. Точка  а
а 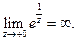
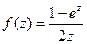 ; 2)
; 2)  ; 3)
; 3)  .
.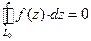 , где
, где 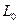 - любой замкнутый контур, лежащий в этой области. Если внутри контура
- любой замкнутый контур, лежащий в этой области. Если внутри контура  , называть вычетом.
, называть вычетом.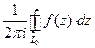 , где
, где 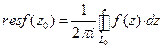 .
.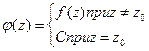 . Тогда по теореме Коши
. Тогда по теореме Коши  . На контуре
. На контуре 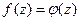 . Поэтому и
. Поэтому и 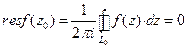 .
. .
.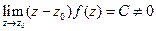 . Отсюда следует, что в окрестности точки
. Отсюда следует, что в окрестности точки 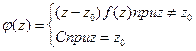 является аналитической. По теореме Коши имеем
является аналитической. По теореме Коши имеем  . Принимая во внимание то, что на контуре
. Принимая во внимание то, что на контуре  , получим
, получим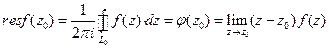 .
.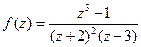 относительно особой точки
относительно особой точки  .
. .
.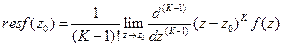 .
.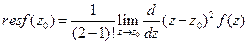 .
. .
.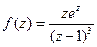 относительно точки
относительно точки 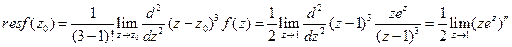 .
.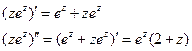 .
.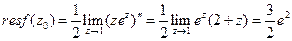 .
. на сумму вычетов относительно особых точек, лежащих внутри контура L.
на сумму вычетов относительно особых точек, лежащих внутри контура L.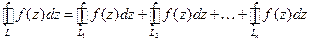 , где
, где  - особые точки,
- особые точки,  - окружности достаточно малых радиусов с центрами в этих точках. Применяя определение вычетов, каждый интеграл правой части можно заменить произведением
- окружности достаточно малых радиусов с центрами в этих точках. Применяя определение вычетов, каждый интеграл правой части можно заменить произведением 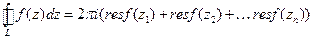 .
. , где L – окружность
, где L – окружность 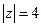 .
.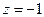 - полюс 2 порядка и
- полюс 2 порядка и  - простой полюс. По основной теореме о вычетах имеем:
- простой полюс. По основной теореме о вычетах имеем: 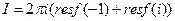 .
.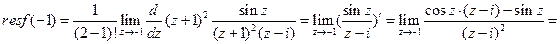
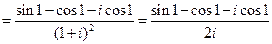 .
.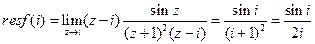 .
. .
. ; б)
; б) 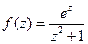 ;
;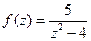 ; д)
; д) 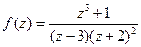 .
. , где L:
, где L: 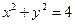 ,
,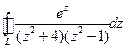 , где L:
, где L:  ,
,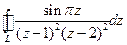 , где L:
, где L: 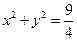 ,
, , где L:
, где L: 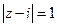 ,
,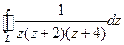 , где L:
, где L: 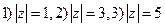 ,
,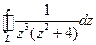 , где L:
, где L:  .
.


