
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие предела и непрерывности функции комплексного переменного в точке.Содержание книги
Поиск на нашем сайте
Допустим, что функция При этом Исключительно важно отметить, что в соответствии с данным определением функция стремится к своему пределу независимо от способа приближения точки Функция Для непрерывности функции Функция называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области. 2.4. Дифференцирование функции комплексного переменного. Условия Эйлера – Даламбера. Пусть задана функция Определение. Производной функции Причем предполагается, что этот предел имеет одно и то же значение независимо от способа стремления приращения аргумента к нулю. Сформулируем исключительно важное условие дифференцируемости функции Теорема. Если функция Эти соотношения называются условиями Эйлера – Даламбера или условиями Коши - Римана. Докажем необходимость этих условий. Предположим, что существует предел Так как этот предел не зависит от направления стремления приращения 1. Предположим, что точка
В этом случае
2. Предположим теперь, что точка В этом случае
Результаты для первого и второго случаев должны быть равными, т.е.
Полученные равенства являются не только необходимыми, но и достаточными условиями дифференцируемости функции комплексного переменного. Определение. Функция Условия Эйлера - Даламбера можно рассматривать как необходимые и достаточные условия аналитичности функции в заданной области. Следует помнить, что под аналитической функцией всегда понимается однозначная функция. Отметим, что все элементарные функции являются аналитическими за исключением отдельных точек. Например, для С учетом условий Эйлера – Даламбера производную дифференцируемой функции можно найти по одной из формул:
Можно доказать, что дифференцирование элементарных функций комплексного переменного можно производить по тем же формулам, по которым дифференцируются соответствующие функции действительного переменного. Пример. Проверить аналитичность функции Решение. По определению Действительная часть функции - Найдем частные производные этих функций.
Из полученных результатов видно, что условия аналитичности выполнены. Производную функции найдем по формуле
2.5. Задачи для самостоятельного решения. 1. Даны комплексные числа 2. Построить области на комплексной плоскости:
3. Вычислить 4. Найти действительные корни уравнения 5. Решить уравнение 6. Найти все комплексные числа, удовлетворяющие условию: 7. Найти образы точек при указанных отображениях.
8. Дана функция 9. Записать в тригонометрической форме комплексные числа: 10. Записать в показательной форме числа:
11. Даны комплексные числа 12. Вычислить 13. Найти все значения
14. Найти: 15. Дана функция 16. Доказать справедливость равенств:
17. Найти 18. Найти решение уравнения 19. Доказать тождество 20. Найти действительную и мнимую часть числа 21. Показать, что функция
22. Доказать справедливость формулы 23. Показать, что функция 24. Найти аналитическую функцию а)
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.13 (0.01 с.) |

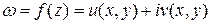 однозначно определена в окрестности точки
однозначно определена в окрестности точки 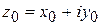 . В этом случае на функцию комплексного переменного можно распространить определение предела для функции действительного переменного, т.е.
. В этом случае на функцию комплексного переменного можно распространить определение предела для функции действительного переменного, т.е. 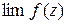
 существует при
существует при 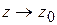 , если существуют пределы:
, если существуют пределы: 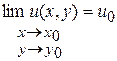 и
и 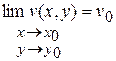 .
.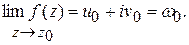
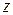 к точке
к точке 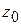 в комплексной области, т. е., если предел существует, то он один и тот же при
в комплексной области, т. е., если предел существует, то он один и тот же при 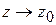 любым способом (по любому пути).
любым способом (по любому пути).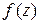 называется непрерывной в точке
называется непрерывной в точке 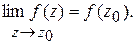
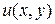 и
и 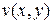 были непрерывны в точке
были непрерывны в точке 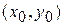 .
.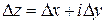 . Получим приращение функции
. Получим приращение функции  . Составим отношение
. Составим отношение 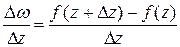 .
.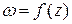 в комплексной области называется предел отношения приращения функции
в комплексной области называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента 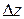 при условии, что приращение аргумента стремится к нулю, т.е.
при условии, что приращение аргумента стремится к нулю, т.е.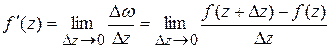 .
.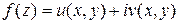 .
.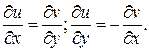
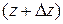 приближается к точке
приближается к точке 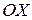 .
.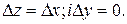

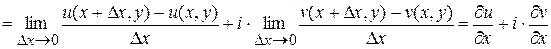 .
.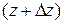 приближается к точке
приближается к точке 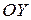 .
.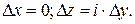
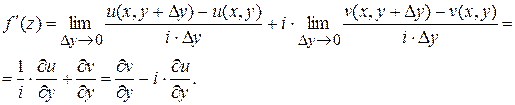
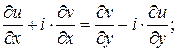 отсюда следует, что
отсюда следует, что 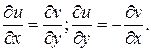
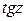 исключаются значения
исключаются значения 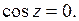
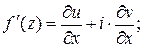

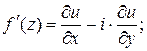
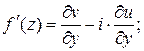
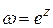 и доказать справедливость формулы
и доказать справедливость формулы 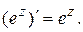
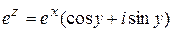 .
.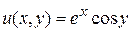 , мнимая -
, мнимая - 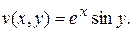

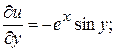
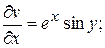
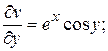
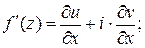
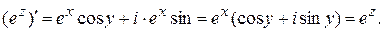
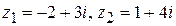 . Найти
. Найти 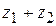 ,
, 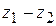 ,
,  ,
, 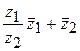 ,
, 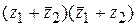 ,
, 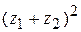 . Построить эти числа на комплексной плоскости.
. Построить эти числа на комплексной плоскости.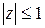 ,
,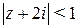 ,
,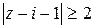 ,
,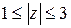 ,
,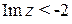 ,
,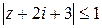 ,
,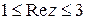 ,
,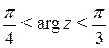 ,
,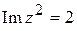 .
.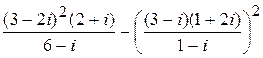 .
.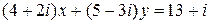 .
.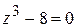 .
.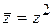 .
. ,
, ,
, .
.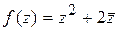 . Вычислить
. Вычислить  .
.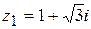 ,
, 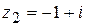 ,
, 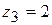 ,
, 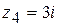 .
.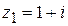 ,
, 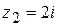 ,
, 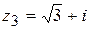 .
.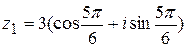 ,
, 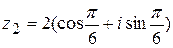 . Найти
. Найти  . Записать результат в алгебраической форме.
. Записать результат в алгебраической форме.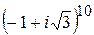 ,
, 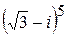 .
.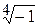 . Изобразить корни на комплексной плоскости.
. Изобразить корни на комплексной плоскости.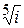 ,
,  ,
, 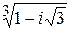 .
.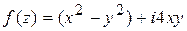 . Вычислить
. Вычислить 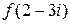 ,
, 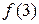 ,
,  .
.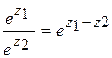 ,
,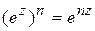 ,
,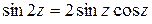 ,
,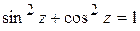 ,
,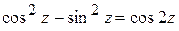 на комплексной плоскости.
на комплексной плоскости.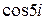 .
.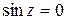 на комплексной плоскости.
на комплексной плоскости.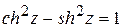 .
.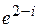 , функции
, функции 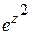 , функции
, функции 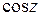 .
.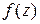 является аналитической на всей комплексной плоскости. Найти ее производную в точке
является аналитической на всей комплексной плоскости. Найти ее производную в точке 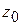
 ,
, ,
, ,
,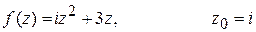 .
.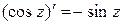 .
.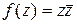 дифференцируема только в точке
дифференцируема только в точке 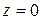 .
.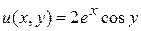 , б)
, б) 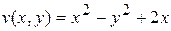 , если
, если 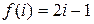 .
.


