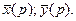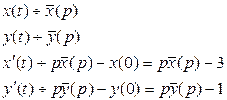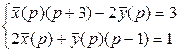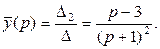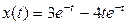Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Элементы теории графов. ⇐ ПредыдущаяСтр 9 из 9
6.1. Основные определения. Графом G (V, E) называется конечное непустое множество вершин V и конечное множество ребер E. Каждое ребро связывает пару вершин. Если ребро e соединяет вершины Два ребра, связывающие одну и ту же пару вершин Степенью вершины графа называется число ребер графа, инцидентных этой вершине (петли считаются дважды). Степень вершины v обозначается d (v). Вершина степени 0 называется изолированной, вершина степени 1 – висячей. Вершина графа называется четной, если ее степень четна, и нечетной, если нечетна. Поскольку ребро, соединяющее вершины Граф называется полным, если каждые две различные его вершины соединены одним и только одним ребром. Матрицей смежности графа G (V, E) называется квадратная матрица А (G) n -го порядка (n – число вершин) с элементами:
Если в графе нет петель, то на главной диагонали матрицы смежности стоят нули. Если же в графе нет кратных ребер, то все элементы матрицы равны либо нулю, либо единице. Матрицей инцидентности графа G (V, E) называется матрица В (G) размера
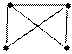
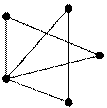
Пример 1. Для графа, изображенного на рисунке, построить матрицы смежности и инцидентности.
Ребро
Таким образом, матрица смежности имеет вид:
Теперь построим матрицу инцидентности В (G). Так как у графа 5 вершин и 9 ребер, матрица В (G) будет размера 5×9. Первое ребро – это петля в первой вершине, поэтому в первом столбце, который соответствует первому ребру, только один элемент
Второе ребро соединяет первую и вторую вершины, следовательно,
Направленные ребра графа, т.е. ребра, для которых определены вершины, из которых они выходят, и вершины, в которые входят, называются дугами. Если все ребра графа направлены, то он называется ориентированным или орграфом. Матрицей смежности ориентированного графа G (V, E) называется квадратная матрица А (G) n -го порядка (n – число вершин) с элементами:
Матрицей инцидентности ориентированного графа G (V, E) называется матрица В (G) размера Пример 2. Построить орграфы по матрицам смежности и инцидентности:
В третьей и пятой строках по три единицы:
Граф G ′ = (V ′, E ′), вершины и ребра которого являются вершинами и ребрами графа G (V, E), т.е. Подграф G ′ = (V ′, E ′) графа G (V, E), являющийся полным графом, называется кликой. Максимальная клика — это клика с максимально возможным числом вершин среди всех существующих клик графа. Дополнением графа G (V, E) называется граф
Объединением графов Пересечением графов
6.2. Задачи для самостоятельного решения. 1. Составить матрицу смежности вершин и матрицу инцидентности графа а) б)
1 4 1 4
2. Изобразить граф, заданный матрицей смежности или матрицей инцидентности. а)
3. Даны графы
4 3 3 2
4 3 3 2 Тема 7. Задачи для контрольных заданий студентов заочной формы обучения. 1. Записать комплексное число Z в алгебраической, тригонометрической и показательной формах. Найти все значения корня n –ной степени из числа Z. 1.1.
1.4.
1.7.
1.10.
2. Представить заданную функцию 2.1.
2.3.
2.5.
2.7.
2.9.
3. Найти, пользуясь таблицей, изображения F (p) данных функций f (t). 3.1. a) f(t) =
3.2 а)
3.3. а)
3.4 а)
3.5. а)
3.6. а)
3.7. а)
3.8. а)
3.9. а)
3.10. а)
4. Найти оригинал f (t) по заданному изображению F(p).
4.1. а)
4.2. а)
4.3. а)
4.4. а)
4.5. а)
4.6. а)
4.7. а)
4.8. а)
4.9. а)
4.10. а)
5. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
5.1.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
6. Найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10. Решение типовых задач. Задача 1. Записать число Решение. 1) Чтобы записать данное число в алгебраической форме
Алгебраическая форма данного числа: 2) Запишем это число в тригонометрической форме В данном числе
Угол, для которого косинус положителен, а синус отрицателен, находится в четвертой четверти. Данное число в тригонометрической форме имеет вид 3) Запишем данное число в показательной форме 4) Найдем все значения
1) к=0
2) к=1
3) к=2
Задача 2. Представить заданную функцию Решение. Воспользуемся формулой
Действительная часть этой функции равна Проверим, выполняются ли условия Эйлера – Даламбера аналитичности данной функции: Найдем частные производные функций u(x,y) и v(x,y) и сравним их.
Видим, что условия Эйлера – Даламбера выполняются. Следовательно, функция является аналитической. Найдем ее производную по формуле
В точке Заметим, что производную можно найти иначе по известным формулам. Мы получили такой же результат. Задача 3. Найти, пользуясь таблицей, изображения F(p) данных функций f(t). а) Решение. а) Представим функцию f(t) в виде: Пользуясь свойством линейности преобразования Лапласа и формулами (9) и (4) получим
б) Воспользуемся формулой (6) и теоремой запаздывания Задача 4. Найти оригинал f(t) по заданному изображению F(p). а) Решение. а) Выделим в знаменателе полный квадрат и преобразуем выражение так, чтобы можно было применить формулы (7) и (8).
По формулам (7) и (8) и свойству линейности получим б) По формулам (2),(4),(1) и свойству линейности получим Задача 5. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Решение. Предположим, что искомая функция и ее производные первого, второго и третьего порядков являются оригиналами. Обозначим искомую функцию x(t), а ее изображение
Чтобы составить вспомогательное уравнение, подставим полученные изображения в данное дифференциальное уравнение. Получим
Выразим из этого уравнения
По полученному изображению определим оригинал – искомую функцию x(t). Чтобы использовать таблицу изображений, представим полученное выражение в виде суммы простейших рациональных дробей.
Это равенство является тождеством, оно верно при любых значениях p. При p=0 получим: А=1. Пусть Значения В, С и D определим методом неопределенных коэффициентов. Для этого приравняем коэффициенты при одинаковых степенях «р» в левой и правой частях равенства (*).
Итак, Пользуясь таблицей, определим оригинал. Искомое частное решение данного дифференциального уравнения имеет вид Задача 6. Найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
Решение. Обозначим искомые функции x(t) и y(t), а их изображения Составим вспомогательную систему уравнений.
Решим систему по правилу Крамера.
Определим искомые функции, используя таблицу преобразований Лапласа. Для этого предварительно преобразуем полученные выражения.
Искомое частное решение данной системы дифференциальных уравнений имеет вид
|
||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.136 (0.169 с.) |
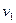 и
и 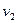 , то говорят, что ребро e и вершины
, то говорят, что ребро e и вершины  и
и  , справедливо соотношение:
, справедливо соотношение:  где m – количество ребер графа.
где m – количество ребер графа.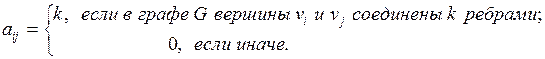
 (n – число вершин, m – число ребер) с элементами:
(n – число вершин, m – число ребер) с элементами:
 Решение: Начнем с построения матрицы смежности А (G). У данного графа пять вершин, следовательно, матрица смежности будет иметь размер 5×5. Поскольку у графа есть петля и она находится в первой вершине, то на главной диагонали элемент
Решение: Начнем с построения матрицы смежности А (G). У данного графа пять вершин, следовательно, матрица смежности будет иметь размер 5×5. Поскольку у графа есть петля и она находится в первой вершине, то на главной диагонали элемент 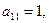 а все остальные
а все остальные 
 соединяет первую и вторую вершины; других ребер, соединяющих эти же вершины, нет, следовательно, элементы
соединяет первую и вторую вершины; других ребер, соединяющих эти же вершины, нет, следовательно, элементы  Аналогично,
Аналогично, 

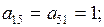

 Ребра
Ребра 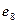 и
и 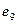 соединяют четвертую и пятую вершины и являются кратными, поэтому
соединяют четвертую и пятую вершины и являются кратными, поэтому 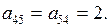 Все остальные элементы
Все остальные элементы  равны нулю.
равны нулю.
 а все остальные нулевые.
а все остальные нулевые. а остальные элементы второго столбца – нулевые. Рассуждая аналогично, получаем матрицу инцидентности:
а остальные элементы второго столбца – нулевые. Рассуждая аналогично, получаем матрицу инцидентности: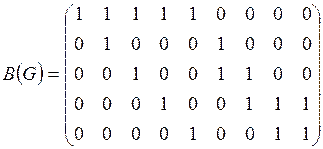 .
.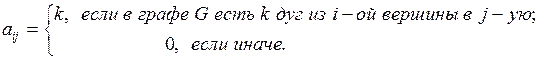


 Решение. 1) Даная матрица смежности – квадратная матрица пятого порядка, следовательно, у рассматриваемого графа пять вершин. Первая и четвертая строки смежной матрицы нулевые, т.е. из первой и четвертой вершин не выходит ни одной дуги. Во второй строке два элемента отличны от нуля, причем,
Решение. 1) Даная матрица смежности – квадратная матрица пятого порядка, следовательно, у рассматриваемого графа пять вершин. Первая и четвертая строки смежной матрицы нулевые, т.е. из первой и четвертой вершин не выходит ни одной дуги. Во второй строке два элемента отличны от нуля, причем, 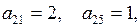 следовательно, из второй вершины выходят три дуги: две в первую вершину и одна в пятую.
следовательно, из второй вершины выходят три дуги: две в первую вершину и одна в пятую. и
и  т.е. из третьей и пятой вершин выходят по три дуги: из третьей вершины – во вторую, четвертую и пятую вершины, а из пятой вершины – в первую, третью и четвертую.
т.е. из третьей и пятой вершин выходят по три дуги: из третьей вершины – во вторую, четвертую и пятую вершины, а из пятой вершины – в первую, третью и четвертую. следовательно, первое ребро выходит из первой вершины и входит во вторую. Второе ребро выходит из первой вершины и входит в третью и т.д.
следовательно, первое ребро выходит из первой вершины и входит во вторую. Второе ребро выходит из первой вершины и входит в третью и т.д.


 называется подграфом графа G.
называется подграфом графа G. , множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е.
, множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е. 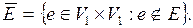
 и
и  таких, что
таких, что  и
и 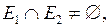 называется граф
называется граф  множеством вершин которого является множество
множеством вершин которого является множество  а множеством ребер – множество
а множеством ребер – множество 
 и
и 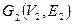 называется граф
называется граф  множеством вершин которого является множество
множеством вершин которого является множество  а множеством ребер – множество
а множеством ребер – множество 

 2 3 2 3
2 3 2 3
 в) г)
в) г) д)
д)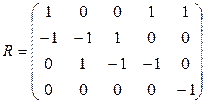 б)
б) 
 и
и  . Найдите
. Найдите  ,
, 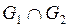 ,
,  . Для графа
. Для графа 
 а)
а)  1 2
1 2  1
1
 1 2
1 2  n=4. 1.2.
n=4. 1.2.  n=3. 1.3.
n=3. 1.3.  n=3.
n=3. n=3. 1.5.
n=3. 1.5.  n=3. 1.6.
n=3. 1.6.  ; n=4.
; n=4. n=4. 1.8.
n=4. 1.8. 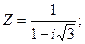 n=3. 1.9.
n=3. 1.9. 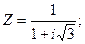 n=3.
n=3.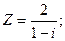 n=4.
n=4. в виде
в виде  Проверить, является ли она аналитической. Если да, то найти значение производной функции
Проверить, является ли она аналитической. Если да, то найти значение производной функции 
 2.2.
2.2. 
 2.4.
2.4. 
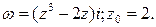 2.6.
2.6. 
 2.8.
2.8. 
 2.10.
2.10. 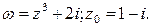
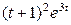 б)
б) 
 б)
б) 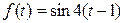
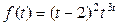 б)
б) 
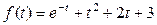 б)
б) 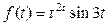
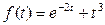 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
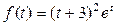 б)
б) 
 б)
б) 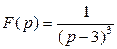
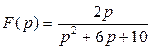 б)
б) 
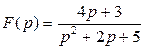 б)
б) 
 б)
б) 
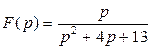 б)
б) 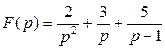
 б)
б) 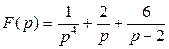
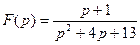 б)
б) 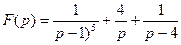
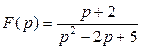 б)
б) 
 б)
б) 
 б)
б) 





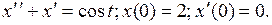





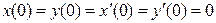
 x(0)=1; y(0)=-1.
x(0)=1; y(0)=-1. x(0)=1; y(0)=0.
x(0)=1; y(0)=0.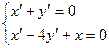 x(0)=1; y(0)=-1.
x(0)=1; y(0)=-1.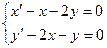 x(0)=2; y(0)=4.
x(0)=2; y(0)=4. x(0)=y(0)=1.
x(0)=y(0)=1. x(0)=2; y(0)=3.
x(0)=2; y(0)=3. x(0)=2; y(0)=3.
x(0)=2; y(0)=3. x(0)=1; y(0)=2.
x(0)=1; y(0)=2.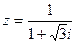 в алгебраической, тригонометрической и показательной формах. Найти все значения
в алгебраической, тригонометрической и показательной формах. Найти все значения  .
.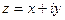 , умножим числитель и знаменатель на число, сопряженное знаменателю.
, умножим числитель и знаменатель на число, сопряженное знаменателю. (Напомним, что
(Напомним, что 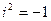 ).
).

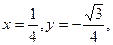





 :
: 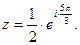

 где к=0,1,2.
где к=0,1,2.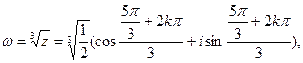 где к=0,1,2.
где к=0,1,2.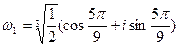
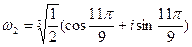

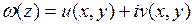 . Проверить, является ли она аналитической. Если да, то найти производную
. Проверить, является ли она аналитической. Если да, то найти производную  в точке
в точке  .
. .
. .
.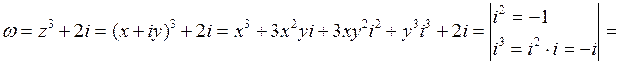
 .
. , мнимая -
, мнимая - 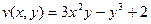 .
.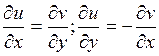 .
.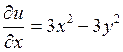 ,
, 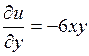 ,
, 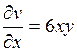 ,
, 
 .
. .
.
 х=1, у=-1.
х=1, у=-1.  .
. .
. , б)
, б)  .
. .
. .
. . Получим
. Получим .
.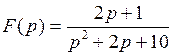 , б)
, б)  .
. .
.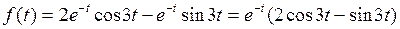 .
. .
. ,
,  .
.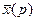 . Найдем изображения левой и правой частей дифференциального уравнения и составим вспомогательное (операторное) уравнение.
. Найдем изображения левой и правой частей дифференциального уравнения и составим вспомогательное (операторное) уравнение.

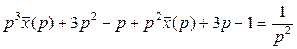


 (*)
(*)

 .
.
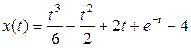 .
.
 x(0)=3, y(0)=1.
x(0)=3, y(0)=1.