
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания по выполнению контрольных работСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Студент должен выполнять контрольные работы по варианту, номер которого ему присваивает преподаватель. При выполнении и оформлении контрольных работ необходимо соблюдать следующие правила: 1. На титульном листе должны быть ясно написаны фамилия студента, его инициалы, номер контрольной работы и дата сдачи работы преподавателю. 2. Контрольная работа выполняется в тетради, а не на листах, обязательно шариковой ручкой (не красной), с полями для замечаний преподавателя. 3. Решения задач контрольной работы располагаются в порядке номеров, указанных в контрольных работах, перед решением задачи должно быть записано полностью ее условие, исходя из данных своего варианта задания. В том случае, когда несколько задач имеют общую формулировку, переписывая условие задачи, следует заменить общие данные конкретными из своего варианта. 4. Каждая задача контрольной работы должна начинаться с новой страницы, в конце решения должен быть обязательно подробный ответ. 5. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов; чертежи можно выполнять от руки. Контрольные работы, выполненные с нарушением изложенных правил или выполненные студентом не по своему варианту, не зачитываются и возвращаются без проверки. Получив от преподавателя проверенную работу, студент должен исправить в ней все отмеченные ошибки и недочеты. Если работа не зачтена, она должна быть в короткий срок либо выполнена заново целиком, либо должны быть заново решены задачи, указанные преподавателем. Исправленную работу следует сдать вместе с незачтенной. Зачтенные контрольные работы предъявляются преподавателю на зачете или экзамене. Контрольные работы №1 и №3 должны быть сданы до 10 декабря текущего учебного года. Контрольные работы №2 и №4 должны быть сданы до 10 мая текущего учебного года.
КОНТРОЛЬНАЯ РАБОТА №1
В задачах 1-20 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В; 4) уравнение медианы АЕ; 5) уравнение и длину высоты CD. Сделать чертеж.
1. А(1; -1), В(4; 3), С(5; 1). 2. А(0; -1), В(3; 3), С(4; 1). 3. А(1; -2), В(4; 2), С(5; 0). 4. А(2; -2), В(5; 2), С(6; 0). 5. А(0; 0), В(3; 4), С(4; 2). 6. А(0; 1), В(3; 5), С(4; 3). 7. А(3; -2), В(6; 2), С(7; 0). 8. А(3; -3), В(6; 1), С(7; -1). 9. А(-1; 1), В(2; 5), С(3; 3). 10. А(4; 0), В(7; 4), С(8; 2). 11. А(2; 2), В(5; 6), С(6; 4). 12. А(4; -2), В(7; 2), С(8; 0). 13. А(0; 2), В(3; 6), С(4; 4). 14. А(4; 1), В(7; 5), С(8; 3). 15. А(3; 2), В(6; 6), С(7; 4). 16. А(-2; 1), В(1; 5), С(2; 3). 17. А(4; -3), В(7; 1), С(8; -1). 18. А(-2; 2), В(1; 6), С(2; 4). 19. А(5; 0), В(8; 4), С(9; 2). 20. А(2; 3), В(5; 7), С(6; 5).
В задачах 21-40 даны координаты вершин пирамиды ABCD. Требуется: 1) записать векторы 2) найти угол между векторами 3) найти проекцию вектора 4) найти площадь грани АВС; 5) найти объем пирамиды ABCD; 6) составить уравнение ребра АС; 7) составить уравнение грани АВС. Сделать чертеж.
21. А(1; 2; 1), В(-1; 5; 1), С(-1; 2; 7), D(1; 5; 9). 22. А(2; 3; 2), В(0; 6; 2), С(0; 3; 8), D(2; 6; 10). 23. А(0; 3; 2), В(-2; 6; 2), С(-2; 3; 8), D(0; 6; 10). 24. А(2; 1; 2), В(0; 4; 2), С(0; 1; 8), D(2; 4; 10). 25. А(2; 3; 0), В(0; 6; 0), С(0; 3; 6), D(2; 6; 8). 26. А(2; 2; 1), В(0; 5; 1), С(0; 2; 7), D(2; 5; 9). 27. А(1; 3; 1), В(-1; 6; 1), С(-1; 3; 7), D(1; 6; 9). 28. А(1; 2; 2), В(-1; 5; 2), С(-1; 2; 8), D(1; 5; 10). 29. А(2; 3; 1), В(0; 6; 1), С(0; 3; 7), D(2; 6; 9). 30. А(2; 2; 2), В(0; 5; 2), С(0; 2; 8), D(2; 5; 10). 31. А(1; 3; 2), В(-1; 6; 2), С(-1; 3; 8), D(1; 6; 10). 32. А(0; 1; 2), В(-2; 4; 2), С(-2; 1; 8), D(0; 4; 10). 33. А(0; 3; 0), В(-2; 6; 0), С(-2; 3; 6), D(0; 6; 8). 34. А(2; 1; 0), В(0; 4; 0), С(0; 1; 6), D(2; 4; 8). 35. А(0; 2; 1), В(-2; 5; 1), С(-2; 2; 7), D(0; 5; 9). 36. А(1; 1; 1), В(-1; 4; 1), С(-1; 1; 7), D(1; 4; 9). 37. А(1; 2; 0), В(-1; 5; 0), С(-1; 2; 6), D(1; 5; 8). 38. А(0; 1; 0), В(-2; 4; 0), С(-2; 1; 6), D(0; 4; 8). 39. А(0; 1; 1), В(-2; 4; 1), С(-2; 1; 7), D(0; 4; 9). 40. А(0; 2; 0), В(-2; 5; 0), С(-2; 2; 6), D(0; 5; 8).
В задачах 41-60 дана система линейных уравнений: Доказать ее совместимость и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) правилом Крамера.
41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. В задачах 61-80 найти пределы функций, не пользуясь правилом Лопиталя.
61. 1) 2) 62. 1) 2) 63. 1) 2) 64. 1) 2) 65. 1) 2) 66. 1) 2) 67. 1) 2) 68. 1) 2) 69. 1) 2) 70. 1) 2) 71. 1) 2) 72. 1) 2) 73. 1) 2) 74. 1) 2) 75. 1) 2) 76. 1) 2) 77. 1) 2) 78. 1) 2) 79. 1) 2) 80. 1) 2)
В задачах 81-90 заданы функция y = f (x) и два значения аргумента 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргументов; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
81. 82. 83. 84. 85.
В задачах 91-100 задана функция y = f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
91. 92. 93. 94. 95.
КОНТРОЛЬНАЯ РАБОТА №2
В задачах 1-20 найти производные
1. а) г) 2. а) г) 3. а) г) 4. а) г) 5. а) г) 6. а) г) 7. а) г) 8. а) г) 9. а) г) 10. а) г) 11. а) г) 12. а) г) 13. а) г) 14. а) г) 15. а) г) 16. а) г) 17. а) г) 18. а) г) 19. а) г) 20. а) г)
В задачах 21-40 найти
21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40.
В задачах 41-60 исследовать методами дифференциального исчисления функцию
41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60.
В задачах 61-80 по условию задачи составить функцию и исследовать ее на экстремум.
61. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объема V. Каковы должны быть высота ведра и радиус его дна, чтобы на его изготовление ушло наименьшее количество жести? 62. Равнобедренный треугольник, вписанный в окружность радиуса R, вращается вокруг прямой, которая проходит через его вершину параллельно основанию. Какова должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем? 63. Прямоугольник вписан в эллипс с осями 2 a и 2 b. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей? 64. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R. 65. Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R. 66. При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность? 67. Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен a. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света? 68. Сосуд, состоящий из цилиндра, заканчивающегося снизу полусферой, должен вмещать 18 л воды. Найти размеры сосуда, при которых на его изготовление пойдет наименьшее количество материала. 69. Требуется поставить палатку данного объема V, имеющую форму прямого кругового конуса. Найти отношение высоты конуса к радиусу его основания, при котором на палатку уйдет наименьшее количество материала. 70. Требуется изготовить открытый цилиндрический бак данного объема V. Стоимость 1 кв. м металла, идущего на изготовление дна бака, равна 71. Каковы должны быть размеры прямоугольника наибольшей площади, вписанного в круг радиуса 6 см? 72. Проволока длиной 40 см согнута в прямоугольник. Каковы должны быть размеры этого прямоугольника, чтобы площадь его была наибольшей? 73. Канал, ширина которого 27 м, под прямым углом впадает в другой канал шириной 64 м. Какова наибольшая длина бревен, которые можно сплавлять по этой системе каналов? 74. Найти наибольший объем цилиндра, у которого полная поверхность равна 75. Найти наибольший объем конуса, образующая которого равна 76. Объем правильной треугольной призмы равен 77. Открытый чан имеет форму цилиндра объема 78. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим? 79. Найти прямоугольник наибольшей площади, если сумма длин его катета и гипотенузы постоянна и равна 4 см. 80. Деталь из листового железа имеет форму равнобедренного треугольника с боковой стороной 10 см. Каким должно быть основание треугольника, чтобы его площадь была наибольшей?
В задачах 81-100 найти неопределенные интегралы.
81. а) г) 82. а) г) 83. а) г) 84. а) г) 85. а) г) 86. а) г) 87. а) г) 88. а) г) 89. а) г) 90. а) г) 91. а) г) 92. а) г) 93. а) г) 94. а) г) 95. а) г) 96. а) г) 97. а) г) 98. а) г) 99. а) г) 100. а) г)
В задачах 101-120 вычислить площадь, ограниченную заданными параболами.
101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 115. 116. 117. 118. 119. 120.
В задачах 121-140 найти несобственные интегралы или доказать их расходимость.
121. 122. 123. 124. 125. 126. 127. 128. 129. 130. 131. 132. 133. 134. 135. 136. 137. 138. 139. 140. КОНТРОЛЬНАЯ РАБОТА №3
В задачах 1-10 вычислить частные производные первого и второго порядков от заданных функций. |
|
| Поделиться: |

 ,
,  ,
,  в системе орт
в системе орт 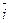 ,
,  ,
,  и найти модули этих векторов;
и найти модули этих векторов;




















 ; а)
; а)  = 2; б)
= 2; б)  .
.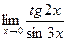 . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3) 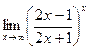 .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а) 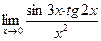 . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3) 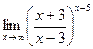 .
. ; а)
; а)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. ; а)
; а)  . 3)
. 3)  .
. и
и  . Требуется:
. Требуется: ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  96.
96. 
 97.
97. 
 98.
98. 
 99.
99. 
 100.
100. 
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 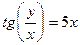 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 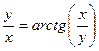 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
;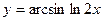 ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в) 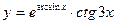 ;
; ; д)
; д)  .
. ; б)
; б)  ; в) в)
; в) в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. для функции заданной параметрически
для функции заданной параметрически  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;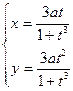 ;
; ;
; ;
;
 ;
; ;
; .
. и, используя результаты, построить ее график.
и, используя результаты, построить ее график. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , а стенок -
, а стенок -  руб. Каковы должны быть радиус дна и высота бака, чтобы затраты на материал для его изготовления были наименьшими?
руб. Каковы должны быть радиус дна и высота бака, чтобы затраты на материал для его изготовления были наименьшими?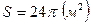 .
. .
. . Какова должна быть длина стороны основания призмы, чтобы ее полная поверхность была наименьшей?
. Какова должна быть длина стороны основания призмы, чтобы ее полная поверхность была наименьшей? . Каковы должны быть радиус основания и высота чана, чтобы на его изготовление ушло наименьшее количество материала?
. Каковы должны быть радиус основания и высота чана, чтобы на его изготовление ушло наименьшее количество материала? ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б) 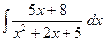 ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
;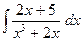 ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 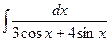 .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
.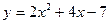 ;
;  ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.


