Приток жидкости к бесконечным цепочкам и кольцевым батареям скважин.

На примере притока жидкости к нескольким рядам или кольцевым батареям скважин ознакомимся с широко применяемым при проектировании разработки нефтяных месторождений методом эквивалентных фильтрационных сопротивлений, предложенным Ю. П. Борисовым и основанным на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Рассмотрим без вывода задачу о притоке жидкости к одной цепочке скважин, расположенных на расстояниях 2 друг от друга и на расстоянии L от прямолинейного контура питания. Пусть на контуре питания задан постоянный потенциал Ф_к, на забоях скважин - потенциал Ф_с (рис. 8). Требуется определить дебит каждой скважины и суммарный дебит n скважин в цепочке.

 

 

Решение задачи заключается в следующем. Цепочка скважин-стоков отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте.

Вдоль прямой АВ, проходящей через скважины (как говорят, вдоль главной линии тока), частицы жидкости будут двигаться наиболее быстро. Прямую А’В’ и ей подобные, делящие расстояние между скважинами пополам, в силу симметрии потока можно рассматривать как непроницаемые границы, вдоль которых движение будет наиболее медленным. Они называются нейтральными линиями тока. Характер распределения потенциалов вдоль этих прямых АВ и А'В' показан на рис. 9.

Задача решается методом суперпозиции. Результаты решения показывают, что на расстоянии от контура питания до половины расстояния между скважинами движение жидкости практически прямолинейное и падение потенциала на этом участке происходит по закону прямолинейной фильтрации. Основное падение потенциала происходит вблизи скважины, где характер движения близок к радиальному. При этом дебит каждой скважины цепочки выражается следующей формулой:

где - гиперболический синус.

В случае, когда , величина очень мала и тогда:

Отсюда следует, что при дебит скважины:

(28)

Вводя обозначения:

формулу (28) представим в виде:

(29)

аналогичному закону Ома.

 

Величина , по терминологии Ю. П. Борисова, называется внешним фильтрационным сопротивлением батареи, - внутренним. Таким образом, приток жидкости к цепочке скважин можно представить схемой эквивалентных фильтрационных сопротивлений, показанной на рис. 10.

Аналогом объемного расхода q служит сила тока, а аналогом разности фильтрационных потенциалов - разность электрических потенциалов. Суммарный дебит всей прямолинейной цепочки из n скважин:

(30)

Из формулы (30) получили выражение для внешнего фильтрационного сопротивления цепочки:

которое представляет собой сопротивление потоку жидкости от контура питания до галереи длиной , расположенной на расстоянии L, от контура питания, а внутреннее сопротивление:

 

выражает сопротивление, возникающее при подходе жидкости к скважинам в зоне радиусом , где фильтрация практически плоскорадиальная. Пусть теперь полубесконечный пласт с прямолинейным контуром питания разрабатывается тремя параллельными цепочками скважин с числом скважин в каждой n₁, n₂, n₃. Пусть скважины в каждой цепочке имеют одинаковые радиусы r_c1, r_c2, r_c3 и забойные давления p_c1, р_c2, р_с3, суммарные дебиты цепочек составляют , , . Схема соответствующих эквивалентных фильтрационных сопротивлений будет теперь разветвленной (рис.11). Расчет схемы проводится аналогично расчету электрических разветвленных цепей по законам Ома и Кирхгофа. Составляются алгебраические линейные уравнения по числу неизвестных (либо дебитов , , , либо забойных давлений p_c1, р_c2, р_с3). При этом очевидно, внешние сопротивления будут равны:

где L₁,L₂, L₃ - расстояния соответственно от контура питания до первой цепочки, между первой и второй цепочками, между второй и третьей цепочками.

Внутренние сопротивления определяются по формулам:

(31)

Отметим, что приток жидкости к трем кольцевым батареям скважин, соосным круговому контуру питания, рассчитывается по той же схеме эквивалентных фильтрационных сопротивлений (см. рис. 11), что и для цепочек скважин.

При этом внешние фильтрационные сопротивления будут выражаться так:

где R₁, R₂, R₃ - радиусы батарей.

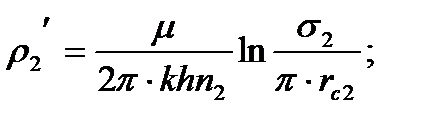
Внутренние фильтрационные сопротивления определяются по формулам (31).