Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель нелинейного накопления поврежденийСодержание книги
Поиск на нашем сайте
Кинетическое уравнение типа (4.15) для параметра поврежденности может быть постулировано в различном виде. Ниже приведен вариант такого уравнения (4.23), принятый в американских стандартах ASTM (American Society of Testing and Materials), и в нем постулируется зависимости скорости роста поврежденности не от эффективного напряжения, а непосредственно от уровня накопленной поврежденности. Данный вариант уравнения рассматривается применительно к циклическому нагружению с постоянной амплитудой. Правило оценки долговечности при переменных амплитудах циклического нагружения, так же принятое в стандартах ASTM, изложено в разделе 4.6. Параметром поврежденности волокнистых композитов ω можно считать любую безразмерную характеристику поврежденного состояния структуры, меняющуюся (от нуля до единицы) в процессе длительного или усталостного нагружения. Желательно, чтобы этот параметр имел некий физический смысл и мог быть оценен в независимом физическом или механическом эксперименте. Напомним, что мы называем механическими моделями те, в которые входят параметры, принципиально определимые в макроэксперименте. К механическим параметрам поврежденности можно отнести: · относительное снижение модуля упругости с ростом поврежденности, которое можно оценивать по снижению напряжений при фиксированном размахе деформации, по снижению скорости распространения упругой волны или по росту собственной частоты изгибных колебаний образца в виде балки с прикрепленной на конце массой, испытываемого на машинах резонансного типа; · нормированное снижение остаточной прочности, определяемой на разных этапах циклического нагружения; · уровень необратимой деформации, определяемой после разгрузки при разных уровнях наработки (после различного числа циклов нагружения); · степень отклонения диаграммы деформирования от линейной, etc. Для анализа поврежденных состояний используют также различные физические методы диагностики и неразрушающего контроля (NDE – Non- Destructive Estimation), с помощью которых оценивают меру поврежденности с позиций материаловедения и физики твёрдого тела. При этом за параметр поврежденности принимают: · интегральную энергию сигналов акустической эмиссии (АЭ); · нормированный максимальный размер поврежденной зоны – зоны расслоения;
· суммарную нормированную длину микротрещин в матрице (в поле зрения микроскопа); · нормированное число разорванных волокон (в поле зрения микроскопа); · нормированное число отслоенных волокон (в поле зрения микроскопа); · etc. (et cetera = и т.д.) При циклическом нагружении с постоянной амплитудой напряжений за аналог текущего времени можно принять отношение текущего числа циклов n к циклической долговечности N для данного режима испытаний: ζ= n / N. В начальный момент ζ=0, в момент разрушения ζ=1. Для параметра поврежденности ω принимаются аналогичные условия: ω=0 при ζ=0 и ω=1 при ζ=1. Далее принимается простейшая гипотеза о линейной зависимости скорости роста параметра поврежденности от текущего уровня поврежденности:
Можно, разумеется, принять в (4.23) нелинейную (степенную) зависимость, но такое усложнение вряд ли оправданно, если учесть значительный разброс экспериментальных данных по циклической долговечности. Качественные эффекты нелинейного накопления повреждений описывает даже такое простое, линейное соотношение. Уравнение (4.23) имеет с точностью до константы
Если K >0 согласно (4.24) происходит вначале медленное, а затем – ускоряющееся накопление повреждений (кривая 3 на рис. 4.3). При K <0 – напротив, происходит насыщение (кривая 2 на рис. 4.3): вначале – быстрое накопление повреждений, а затем – замедленное. При K =0 уравнение (4.23) вырождается в правило линейного суммирования повреждений (раздел 4.5): параметр поврежденности ω тождественно превращается в нормированное число циклов ζ, которое иногда принимают за простейший параметр поврежденности.
Рис. 4.3. Варианты роста параметра поврежденности ω с ростом нормированного числа циклов ζ: 1 — K = 0; 2 — K < 0; 3 — K > 0 Кривая 3 на рис. 4.3 напоминает характер нарастания суммарной энергии акустической эмиссии, что позволяет связать АЭ с накоплением повреждений, а следовательно, использовать анализ АЭ как средство диагностики критических состояний – не только образцов, но и композитных элементов конструкций летательных аппаратов. По достижению углом наклона графика роста суммарной энергии сигналов АЭ (типа 3 на рис. 4.3) критического уровня можно судить о начале неустойчивого (катастрофического) роста поврежденности, который приведет к окончательному разрушению. Такого рода алгоритмы призваны служить основой бортовой системы аварийной защиты, предсказывающей приближение критических состояний авиационных конструкций.
|
||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.119.128 (0.01 с.) |

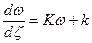
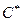 решение
решение 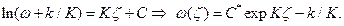 Определяя эту константу
Определяя эту константу 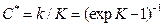 из начальных условий, находим окончательно
из начальных условий, находим окончательно