
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные значения и собственные функции оператора Гамильтона. Квантование энергии микрочастиц⇐ ПредыдущаяСтр 15 из 15
Гамильтониан (оператор Гамильтона) — оператор причем, для свободной частицы (не находящейся в потенциальном поле) Π ≡ 0. В этих терминах решение уравнения Шредингера сводится к задаче о собственных значениях и собственных функциях оператора где, соответственно, ψ — собственная функция, а E — собственное число Уравнение Шрёдингера для гармонического осциллятора имеет вид где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что это уравнение имеет конечные, однозначные и непрерывные решения
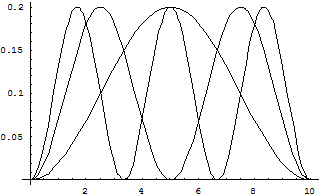
На рис. дана схема энергетических уровней осциллятора. Для наглядности уровни вписаны в кривую потенциальной энергии. Однако, следует помнить, что в квантовой механике полная энергия не может быть представлена в виде точно определённых кинетической и потенциальной энергий. Уровни энергии здесь являются эквидистантными — отстоящими друг от друга на одинаковое расстояние. Наименьше возможное значение энергии равно Квантовомеханический расчет показывает, что для гармонического осциллятора возможны только переходы между соседними уровнями. При таких переходах квантовое число n изменяется на единицу:
Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора.
Поступив похожим образом, для некоторой микрочастицы можно найти решения (2) в виде где n — целое число. Значения энергии частицы En в этом случае также изменяются скачком (квантуются). Смысл волновой функции Как показал Борн (1928), волновую функцию следует интерпретировать следующим образом: квадрат модуля Ψ определяет вероятность d w нахождения частицы в элементе объема d V: где Согласно такой интерпретации, нахождение частицы в интервале (−∞,∞) есть достоверное событие: где A — коэффициент нормировки, равный
Функция Ψ1 с таким множителем называется нормированной, и для нее
Выражение «бесконечно высокие стенки» означает, что вероятность нахождения частицы вне интервала (0, l) равна нулю, т.е. По постановке задачи, частица движется в области (0, l). Внутри этой области U =0, а на границах U (0)= U (l)=∞. В случае одномерного движения
и, следовательно, уравнение Шредингера имеет вид Обозначим
Тогда, с учетом обозначений, (2) перепишется в виде Это уравнение гармонического осциллятора, и мы знаем его решения: Возьмем Тогда для энергии частицы будем иметь Энергия частицы изменяется скачком между ближними уровнями. При этом
График для En представлен на рисунке справа.
Произведем нормировку полученного решения (5). Согласно условию нормировки
Отсюда
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.140 (0.007 с.) |
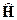 , определяющий изменение во времени состояния квантовой системы (ее волновой функции Ψ), то есть вид уравнения Шредингера. Одновременно гамильтониан является оператором полной энергии системы (если потенциальная функция Π не зависит от времени). Согласно определению
, определяющий изменение во времени состояния квантовой системы (ее волновой функции Ψ), то есть вид уравнения Шредингера. Одновременно гамильтониан является оператором полной энергии системы (если потенциальная функция Π не зависит от времени). Согласно определению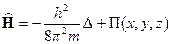 , (1)
, (1)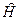 :
: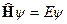 , (2)
, (2) (3)
(3)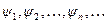 при значениях параметра Е равных
при значениях параметра Е равных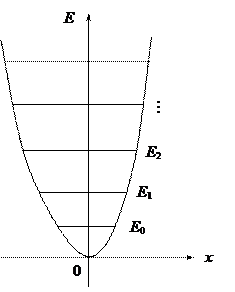
 (4)
(4)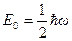 (5) Это значение называется нулевой энергией. Существование нулевой энергии подтверждается экспериментами по рассеянию света кристаллами при низких температурах. Оказывается, что интенсивность рассеянного света по мере понижения температуры стремится не к нулю, а к некоторому конечному значению, указывающему на то, что при абсолютном нуле колебания атомов в решётке не прекращаются.
(5) Это значение называется нулевой энергией. Существование нулевой энергии подтверждается экспериментами по рассеянию света кристаллами при низких температурах. Оказывается, что интенсивность рассеянного света по мере понижения температуры стремится не к нулю, а к некоторому конечному значению, указывающему на то, что при абсолютном нуле колебания атомов в решётке не прекращаются.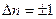 . (6)
. (6)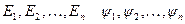 , (7)
, (7)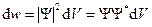 , (1)
, (1)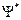 — комплексно-сопряженная функция.
— комплексно-сопряженная функция.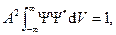 (2)
(2)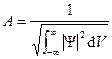 .
.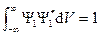 . (3)
. (3) §6. Простейшая задача квантовой механики: частица в потенциальной яме с бесконечно высокими стенками
§6. Простейшая задача квантовой механики: частица в потенциальной яме с бесконечно высокими стенками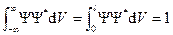 (1)
(1)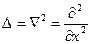 ,
,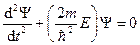 . (2)
. (2) . (3)
. (3)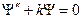 . (4)
. (4) либо
либо  . (5)
. (5)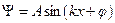 , где A — нормировочный множитель, φ — начальная фаза. Так как стенки непроницаемы, то должно быть
, где A — нормировочный множитель, φ — начальная фаза. Так как стенки непроницаемы, то должно быть 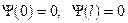 . Отсюда получим
. Отсюда получим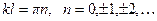 (6)
(6)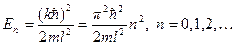 (7)
(7)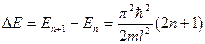 . (8)
. (8) Для свободной частицы l →∞, En →0.
Для свободной частицы l →∞, En →0.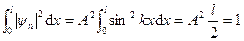 .
.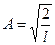 ,
, 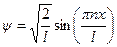 . (9)
. (9)


