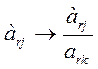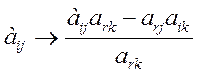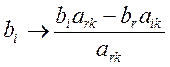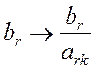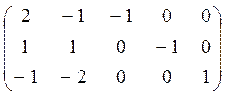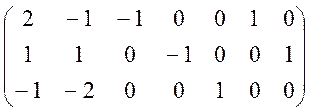Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы решения задач с помощью симплекс-метода с естественным базисомСодержание книги
Поиск на нашем сайте
1. Привести задачу к канонической форме (знаки «=» в функциональных ограничениях и хi ≥ 0). 2. Записать матрицу функциональных ограничений так, чтобы в её составе была единичная матрица. При этом получаем допустимое решение. 3. Проверить допустимое решение на оптимальность с помощью симплекс-разности: Δj = Σ ciaij - сj. Если для всех векторов Δj ≥ 0, то решение оптимально. 4. Если решение неоптимальное, то в него вводим вектор (Ак), дающий минимальную величину симплекс-разности Δк (к - номер разрешающего столбца). Если все компоненты вводимого в базис вектора ≤ 0, то задача решений не имеет. 5. Определить вектор (Аr), который должен быть выведен из базиса, для этого вычислить отношение Q = min Элемент а rk – разрешающий элемент. 6. Пересчитать элементы матрицы функциональных ограничений по формулам:
(Проиллюстрировать правило прямоугольника.)
Примечание. Для использования приведенной процедуры к минимизации линейной функции f (x1,x2,…, xn) следует искать максимум «-f(x1,x2,…, xn)», затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.
Пример. Получить решение по модели:
1 этап. Эта задача (модель) линейного программирования, приведем ее к каноническому виду путем введения дополнительных переменных x 3 и x4:
2 этап.
КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0,0,300,150). 3 этап. Проверяется оптимальность полученного плана. Расчеты оформляются в симплекс-таблицах:
Т.к. среди симплекс-разностей есть отрицательные, то полученный план не оптимален. 4 этап. Т.к. минимальная величина симплекс-разности соответствует вектору А2, то он войдет в базис. Второй столбец – разрешающий. Этап. Считаем величину Q. Q = min
Т.к. минимальная величина Q соответствует вектору А3, то выйдет из базиса вектор А3. Первая строка - разрешающая. Элемент а12 – разрешающий элемент. 6 этап. Пересчитываем элементы матрицы функциональных ограничений по формулам:
Далее повторяем этапы 2-6 до получения оптимального решения.
В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности неотрицательны. Оптимальные значения переменных равны: x1*=75, x2* =75 (основные переменные), x3*= 0, x4*= 0 (дополнительные переменные). Максимальное значение целевой функции равно 375.
Симплекс-метод с искусственным базисом (М-метод) применяется в тех случаях, когда затруднительно найти первоначальный опорный план канонической формы задачи ЛП. Этот метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной: 1. добавлением к матрице коэффициентов функциональных ограничений таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов. 2. в линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М- достаточно большое число.
В полученной задаче первоначальный опорный план очевиден. Как решать М-задачу: обычным симплекс-методом, но 1. В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу.
2. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача (либо максимум бесконечен, либо условия задачи противоречивы). Пример. Решить ЗЛП по модели: min f(х) = 10х1 – 5х2 2х1 – х2 ≥ 3 х1 + х2 ≥ 2 х1 + 2х2 ≥ -1 х1,2 ≥ 0. 1 этап. Эту ЗЛП приведем к каноническому виду и одновременно перейдем к задаче «на максимум». max (- 10х1 + 5х2) 2х1 – х2 –х3 = 3 х1 + х2 - х4 = 2 -х1 - 2х2 + х5 = 1 х1,2,3,4,5 ≥ 0.
2 этап. Запишем матрицу коэффициентов функциональных ограничений.
А1 А2 А3 А4 А5 Если умножить на «-1» 1 и 2 строки, то станут отрицательными правые части (а это недопустимо) Для нахождения опорного плана переходим к М - задаче: вводим искусственные единичные вектора в матрицу
А1 А2 А3 А4 А5 Р1 Р2 Изменяем целевую функцию. max (- 10х1 + 5х2 – Му1 - Му2) Дальнейшее решение проводим в симплекс-таблицах:
Полученный оптимальный план не единственный, т.к. нулевая оценка симплекс-разности соответствует вектору А4, не входящему в базис. Особые случаи решения ЗЛП 1. Если все компоненты вектора, подлежащего вводу в базис не положительны, то ЗЛП решений не имеет вследствие неограниченности сверху целевой функции: 2. Если нулевая оценка симплекс-разности соответствует вектору, не входящему в базис, то в общем случае это означает, что оптимальный план не единственный.
2.1.6 Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана Каждой задаче линейного программирования соответствует другая задача, называемая двойственной по отношению к исходной. Актуальность темы: Для чего составляют и решают двойственные задачи? – для того, чтобы провести анализ решения исходной задачи, а именно, ответить на следующие вопросы: 1. Какой ресурс более дефицитен в отношении принятого в задаче показателя эффективности и, следовательно, больше сдерживает рост прибыли? 2. Как изменится прибыль при изменении запаса ресурсов? 3. Каковы нормы заменяемости ресурсов (не абсолютные, а относительные, т.е. рассматриваемые с точки зрения конечного эффекта)? 4. Выгодно или нет вводить в план производства новые изделия? Сегодня мы будем с вами составлять и решать двойственную задачу, отвечать на эти вопросы. Заметим, что 2-ая задача контрольной работы – задача, решаемая с использованием теории двойственности. Ранее была рассмотрена задача ЛП об использовании ограниченных ресурсов (Тема 1.). Запишем модель задачи ЛП в общем виде для для m- видов сырья и n- видов продукции.
Назовем ее задача I (исходная). Рядом запишем модель двойственной задачи.
Экономическая интерпретация прямой задачи следующая: составить такой план выпуска продукции X=(x1,x2,…,xn), при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов. Рассмотрим экономическую интерпретацию двойственной задачи. Предположим, что некоторая организация решила закупить ресурсы S1,S2,…,Sm предприятия и необходимо установить оптимальные цены на эти ресурсы: обозначим их y1,y2,…,ym. 1) Покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z были минимальны: Z = b1y1 + b2y2 +…+ bmym → min 2) С другой стороны, предприятие, продающее ресурсы, заинтересовано в том чтобы полученная прибыль (выручка) от продажи ресурса была не меньше той суммы, которую предприятие может получить при переработке сырья в готовую продукцию. Запишем это условие отдельно для каждого вида продукции: a11y1 + a21y2 + …+ am1ym ≥ c1,- для первого вида продукции (выручка от продажи сырья, необходимого для производства единицы продукции первого вида, должна быть больше или равна прибыли от реализации единицы продукции первого вида) a12y1 + a22y2 + …+ am2ym ≥ c2, - для второго вида продукции ……………………………… a1ny1 + a2ny2 + …+ amnym ≥ cn, - для n-ого вида продукции.
3) В результате учета интересов двух сторон (покупателя и продавца) мы получаем вторую задачу: Найти такой набор цен (оценок) ресурсов Y =(y 1, y 2,…, ym), при котором общие затраты на ресурсы будут минимальными при условии, что выручка от продажи ресурсов будет не меньше той суммы, которую предприятие может получить при переработке сырья в готовую продукцию.
Цены ресурсов y1,y2,…,ym в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что это условные, «ненастоящие» цены, определяемые в результате решения задачи. Поэтому их чаще называют оценками ресурсов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.149 (0.021 с.) |

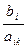 =
= 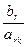 , где
, где 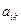 ≥ 0, (r – номер разрешающей строки).
≥ 0, (r – номер разрешающей строки).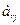 →
→ 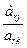
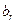 →
→ 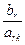

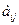 →
→ 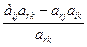
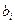 →
→ 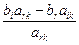
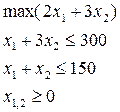
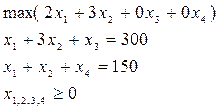
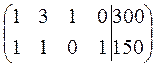 Запишем матрицу коэффициентов функциональных ограничений.
Запишем матрицу коэффициентов функциональных ограничений.