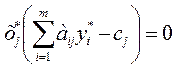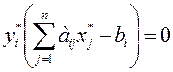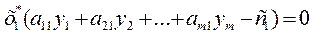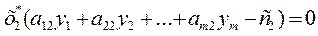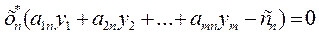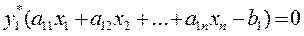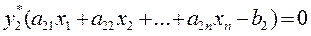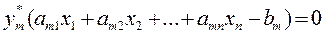Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимно-двойственные задачи линейного программирования и их свойстваСодержание книги
Поиск на нашем сайте
Рассмотрим формально две задачи I и II линейного программирования, представленные выше в таблице. Обе задачи обладают следующими свойствами: 1. В одной задаче ищут максимум линейной функции, в другой – минимум. 2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой. 3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида «<=», а в задаче минимизации – все неравенства вида «>=». 4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу. 5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче. 6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами. В дальнейшем мы будем называть их просто двойственными задачами.
Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи: 1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду «<=», а если минимум – к виду «>=». Для этого неравенства, в которых данное требование не выполняется, умножить на -1. 2. Составить расширенную матрицу А1, в которую включить матрицу коэффициентов при переменных А, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции. 3. Найти матрицу А1`, транспонированную к матрице А1. 4. Сформулировать двойственную задачу на основании полученной матрицы А1` и условия неотрицательности переменных. Пример. F = -7х1 + 2х2 → max При ограничениях
-х1 + 4х2 ≤ 24 х1 - х2 ≥ 6 х1, х2 ≥ 0 Решение: 1. Т.к. исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду ≤, для чего обе части первого и третьего неравенства умножим на «-1». Получим
-х1 + 4х2 ≤ 24 - х1 + х2 ≤- 6 2. Составим расширенную матрицу системы
-7 2 F 3. Найдем матрицу А1`, транспонированную к А.
3 -1 -1 -7
-1 24 -6 Z
4.Сформулируем двойственную задачу: Z = -у1 + 24у2 -6у3 → min При ограничениях
-5у1 +4у2 +у3 ≥ 2 у1, у2, у3 ≥ 0.
Теоремы двойственности и их использование для анализа оптимальных решений
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. Теорема 1. Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны: max F(x) = min Z(y). Если одна из двойственных задач неразрешима, то неразрешима и другая. Теорема 2. Пусть Х=(х1,х2,…,хn) – допустимое решение прямой задачи, У=(у1,у2,…,уm) – допустимое решение двойственной задачи. Для того, чтобы они были оптимальными решениями соответствующих взаимно-двойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
. . .
Если хj ≠ 0, то соответствующее ограничение дв. задачи – строгое равенство.
. . .
Если запас i-ого ресурса израсходован не полностью, то уi = 0.
Теорема об оценках. Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений – неравенств прямой задачи на величину ∆f(Х): ∆f(Х) =∆biyi
Пример использования теорем и свойств двойственных оценок для анализа оптимальных решений. На станках трех видов С1,С2, С3 последовательно обрабатываются детали четырех видов D1, D2, D3, D4. Известно, сколько часов каждая деталь изготавливается на каждом станке, сколько времени может отработать каждый станок и какая прибыль может быть получена при продаже одной детали каждого вида. Данные для решения задачи содержатся в таблице.
Симплекс-методом найден оптимальный план задачи по критерию «максимум прибыли», предусматривающий выпуск трех деталей второго вида и одной детали третьего вида.
х1*= 0 х2*= 3 х3*= 1 х4*= 0 Дать экономико-математический анализ оптимального плана.
Решение. Обозначим хj – объем выпуска деталей j- ого вида (j = 1,2,3,4) и запишем математическую модель задачи по критерию «максимум прибыли»:
max (3х1 + 4х2 + 3х3 + х4) 2х1 + 4х2 + 8х4 ≤ 12 7х1 + 2х2 + 2х3 + 6х4 ≤ 8 5х1 + 8х2 + 4х3 + 3х4 ≤ 48 х1, х2, х3, х4 ≥ 0
Двойственная задача имеет вид: min (12y1 + 8y2 + 48y3) 2y1 + 7y2 + 5y3 ≥ 3 4y1 + 2y2 + 8y3 ≥4 2y2 + 4y3 ≥ 3 8y1 + 6y2 + 3y3 ≥ 1 y1, y2, y3, ≥ 0
Для нахождения оценок y1, y2, y3 используем вторую теорему двойственности. Для этого в ограничения прямой задачи подставим значения оптимального плана. 2*0 + 4*3 + 8*0 =12 7*0 + 2*3 + 2*1 + 6*0 = 8 5*0 + 8*3 + 4*1 + 3*0 = 28 < 48 Поскольку третье ограничение выполняется как строгое неравенство, то у3 = 0. Т.к. х2 > 0 и х3 > 0, то второе и третье ограничения двойственной задачи – строгие равенства: 4y1 + 2y2 + 8y3 = 4 2y2 + 4y3 = 3 Итак, для получения двойственных оценок имеем систему линейных уравнений: у*3 = 0 4y*1 + 2y*2 + 8y*3 = 4 2y*2 + 4y*3 = 3, т.е. у*1 = 0,25; у*2 = 1,5; у*3 = 0.
Вычислим значения целевых функций прямой и двойственной задачи: F (х*) = Z (у*) = 15. По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.
Экономико-математический анализ оптимальных решений базируется на свойствах двойственных оценок. В пределах устойчивости двойственных оценок имеют место следующие свойства. 1. Величина двойственной оценки того или иного ресурса показывает на сколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу. В рассматриваемом примере увеличение фонда времени работы станка С1 на 1 час привело бы к росту максимальной суммы прибыли на 0,25 у. е. (у*1 = 0,25), а увеличение фонда рабочего времени третьего станка не повлияет на оптимальный план выпуска продукции и сумму прибыли. 2. Двойственные оценки отражают сравнительную дефицитность различных ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем не дефицитны (избыточны). В нашем примере недефицитным ресурсом является фонд рабочего времени станка С3 поскольку у*3 = 0. Острее ощущается дефицитность ресурса С2 (у*2 = 1,5), он более дефицитен, чем ресурс С1 (у*1 = 0,25). 3. Двойственные оценки позволяют определять своеобразные «нормы заменяемости ресурсов»: имеются в виду не абсолютная заменяемость ресурсов, а относительная, т.е. заменяемость с точки зрения конечного эффекта и лишь в конкретных условиях данной задачи. В нашем примере относительная заменяемость ресурсов определяется соотношением 0,25: 1,5 = 1: 6. 4. С помощью двойственных оценок можно определять выгодность производства новых изделий: если Предположим в нашем примере следует решить вопрос о целесообразности включения в программу производство деталей нового (пятого) вида при затратах ресурсов станков: 8, 2 и 3 соответственно и ожидаемой удельной прибыли 6 у.е. ∆5 = 0,25 * 8 + 1,5 * 2 + 0 * 3 – 6 = - 1 < 0 – выгодно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.167.85 (0.006 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||

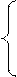 -3х1 + 5х2 ≥ 1,
-3х1 + 5х2 ≥ 1,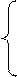 3х1 - 5х2 ≤ - 1,
3х1 - 5х2 ≤ - 1,

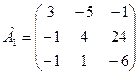



 А1` = -5 4 1 2
А1` = -5 4 1 2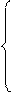 3у1 -у2 -у3 ≥ -7
3у1 -у2 -у3 ≥ -7