Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гоу впо всероссийский заочный финансово- экономический институтСтр 1 из 7Следующая ⇒
ГОУ ВПО ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО- ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ПРИКЛАДНЫЕ МОДЕЛИ
Тема 2. Методы получения оптимальных решений 6 часов.
Подготовила преподаватель кафедры Горбатенко Е.Н. (филиал в г. Владимире)
2008 Тема: Методы получения оптимальных решений План 2.1 Основы линейного программирования. 2.1.1 Математический аппарат линейного программирования. 2.1.2 Различные формы записи задачи линейного программирования. 2.1.3 Графическое решение задачи линейного программирования, исследование случаев неразрешимости задачи. 2.1.4 Основы симплекс-метода, процедуры решения с естественным и искусственным базисом. 2.1.5 Особые случаи решения ЗЛП. 2.1.6 Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана. 2.2 Специальные задачи линейного программирования. 2.2.1 Экономико-математическая модель транспортной задачи. 2.2.2 Модели целочисленного линейного программирования (задачи о назначениях, инвестициях и т.п.) 2.3 Основные понятия и общие сведения о методах реализации моделей нелинейного программирования.
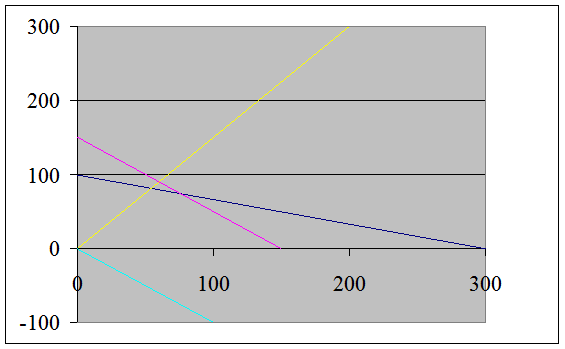
Основы линейного программирования. Пример. Решить графическим методом следующую ЗЛП: f(х1,х2) = (2х1+3х2) → max х1+3х2 £ 300 х1+х2 £ 150 х1,2 ³ 0 Прямые ограничения означают, что область решений будет лежать в первой четверти Декартовой системы координат. Этап 1. Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой х1+3х2 =300. Построим прямую по двум точкам (0;100) и (300;0). Множество решений строгого неравенства – одна из полуплоскостей, на которую делит плоскость построенная прямая. Какая из них является искомой, можно выяснить при помощи одной контрольной точки. Если в произвольно взятой точке, не принадлежащей прямой, неравенство выполняется, то оно выполняется и во всех точках той полуплоскости, которой принадлежит контрольная точка, и не выполняется во всех точках другой полуплоскости. В качестве контрольной точки удобно брать начало координат. Подставим значение координат (0;0) в неравенство, получим 0<300, т.е. оно выполняется. Следовательно, областью решения неравенства служит нижняя полуплоскость.
Аналогичным образом построим ОДР второго неравенства. х1+х2 = 150 Точки (0;150) и (150;0). х1+х2 < 150, при х1 = х2 = 0 неравенство 0 < 150 выполняется, область решения – нижняя полуплоскость. Заштрихуем общую область для всех неравенств, обозначим вершины многоугольника латинскими буквами А, В, С.
Этап 2. Для определения направления движения к оптимуму построим вектор-градиент, соединив его вершину ∆(100;150) с началом координат О (0;0). Этап 3. Построим прямую (линию уровня), перпендикулярную вектору-градиенту. Будем передвигать линию уровня до ее пересечения с точкой В. Далее она выходит из ОДР. Следовательно, именно в этой точке достигается максимум целевой функции. Этап 4. Координаты точки В найдем, решив систему из двух уравнений:
х1+х2 = 150 х1 = 75 х2 = 75 Координаты точки А (0;100) и точки С (150,0).
Т.к. координаты точки В равны х1 = 75 и х2 = 75, то максимум ЦФ равен 375.
      
Основы симплекс-метода, Этап. Считаем величину Q. Q = min
Т.к. минимальная величина Q соответствует вектору А3, то выйдет из базиса вектор А3. Первая строка - разрешающая. Элемент а12 – разрешающий элемент. 6 этап. Пересчитываем элементы матрицы функциональных ограничений по формулам:
Далее повторяем этапы 2-6 до получения оптимального решения.
В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности неотрицательны. Оптимальные значения переменных равны: x1*=75, x2* =75 (основные переменные), x3*= 0, x4*= 0 (дополнительные переменные). Максимальное значение целевой функции равно 375.
Симплекс-метод с искусственным базисом (М-метод) применяется в тех случаях, когда затруднительно найти первоначальный опорный план канонической формы задачи ЛП. Этот метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной: 1. добавлением к матрице коэффициентов функциональных ограничений таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов. 2. в линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М- достаточно большое число.
В полученной задаче первоначальный опорный план очевиден. Как решать М-задачу: обычным симплекс-методом, но 1. В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. 2. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача (либо максимум бесконечен, либо условия задачи противоречивы). Пример. Решить ЗЛП по модели: min f(х) = 10х1 – 5х2 2х1 – х2 ≥ 3 х1 + х2 ≥ 2 х1 + 2х2 ≥ -1 х1,2 ≥ 0. 1 этап. Эту ЗЛП приведем к каноническому виду и одновременно перейдем к задаче «на максимум». max (- 10х1 + 5х2) 2х1 – х2 –х3 = 3 х1 + х2 - х4 = 2 -х1 - 2х2 + х5 = 1 х1,2,3,4,5 ≥ 0.
2 этап. Запишем матрицу коэффициентов функциональных ограничений.
А1 А2 А3 А4 А5 Если умножить на «-1» 1 и 2 строки, то станут отрицательными правые части (а это недопустимо) Для нахождения опорного плана переходим к М - задаче: вводим искусственные единичные вектора в матрицу
А1 А2 А3 А4 А5 Р1 Р2 Изменяем целевую функцию. max (- 10х1 + 5х2 – Му1 - Му2) Дальнейшее решение проводим в симплекс-таблицах:
Полученный оптимальный план не единственный, т.к. нулевая оценка симплекс-разности соответствует вектору А4, не входящему в базис. Особые случаи решения ЗЛП
1. Если все компоненты вектора, подлежащего вводу в базис не положительны, то ЗЛП решений не имеет вследствие неограниченности сверху целевой функции: 2. Если нулевая оценка симплекс-разности соответствует вектору, не входящему в базис, то в общем случае это означает, что оптимальный план не единственный.
2.1.6 Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана Каждой задаче линейного программирования соответствует другая задача, называемая двойственной по отношению к исходной. Актуальность темы: Для чего составляют и решают двойственные задачи? – для того, чтобы провести анализ решения исходной задачи, а именно, ответить на следующие вопросы: 1. Какой ресурс более дефицитен в отношении принятого в задаче показателя эффективности и, следовательно, больше сдерживает рост прибыли? 2. Как изменится прибыль при изменении запаса ресурсов? 3. Каковы нормы заменяемости ресурсов (не абсолютные, а относительные, т.е. рассматриваемые с точки зрения конечного эффекта)? 4. Выгодно или нет вводить в план производства новые изделия? Сегодня мы будем с вами составлять и решать двойственную задачу, отвечать на эти вопросы. Заметим, что 2-ая задача контрольной работы – задача, решаемая с использованием теории двойственности. Ранее была рассмотрена задача ЛП об использовании ограниченных ресурсов (Тема 1.). Запишем модель задачи ЛП в общем виде для для m- видов сырья и n- видов продукции. Назовем ее задача I (исходная). Рядом запишем модель двойственной задачи.
Экономическая интерпретация прямой задачи следующая: составить такой план выпуска продукции X=(x1,x2,…,xn), при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов. Рассмотрим экономическую интерпретацию двойственной задачи. Предположим, что некоторая организация решила закупить ресурсы S1,S2,…,Sm предприятия и необходимо установить оптимальные цены на эти ресурсы: обозначим их y1,y2,…,ym. 1) Покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z были минимальны: Z = b1y1 + b2y2 +…+ bmym → min 2) С другой стороны, предприятие, продающее ресурсы, заинтересовано в том чтобы полученная прибыль (выручка) от продажи ресурса была не меньше той суммы, которую предприятие может получить при переработке сырья в готовую продукцию. Запишем это условие отдельно для каждого вида продукции: a11y1 + a21y2 + …+ am1ym ≥ c1,- для первого вида продукции (выручка от продажи сырья, необходимого для производства единицы продукции первого вида, должна быть больше или равна прибыли от реализации единицы продукции первого вида) a12y1 + a22y2 + …+ am2ym ≥ c2, - для второго вида продукции ……………………………… a1ny1 + a2ny2 + …+ amnym ≥ cn, - для n-ого вида продукции.
3) В результате учета интересов двух сторон (покупателя и продавца) мы получаем вторую задачу: Найти такой набор цен (оценок) ресурсов Y =(y 1, y 2,…, ym), при котором общие затраты на ресурсы будут минимальными при условии, что выручка от продажи ресурсов будет не меньше той суммы, которую предприятие может получить при переработке сырья в готовую продукцию.
Цены ресурсов y1,y2,…,ym в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что это условные, «ненастоящие» цены, определяемые в результате решения задачи. Поэтому их чаще называют оценками ресурсов.
Пример. F = -7х1 + 2х2 → max При ограничениях
-х1 + 4х2 ≤ 24 х1 - х2 ≥ 6 х1, х2 ≥ 0 Решение: 1. Т.к. исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду ≤, для чего обе части первого и третьего неравенства умножим на «-1». Получим
-х1 + 4х2 ≤ 24 - х1 + х2 ≤- 6 2. Составим расширенную матрицу системы
-7 2 F 3. Найдем матрицу А1`, транспонированную к А.
3 -1 -1 -7
-1 24 -6 Z
4.Сформулируем двойственную задачу: Z = -у1 + 24у2 -6у3 → min При ограничениях
-5у1 +4у2 +у3 ≥ 2 у1, у2, у3 ≥ 0.
Теоремы двойственности и их использование для анализа оптимальных решений
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. Теорема 1. Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны: max F(x) = min Z(y). Если одна из двойственных задач неразрешима, то неразрешима и другая.
Теорема 2. Пусть Х=(х1,х2,…,хn) – допустимое решение прямой задачи, У=(у1,у2,…,уm) – допустимое решение двойственной задачи. Для того, чтобы они были оптимальными решениями соответствующих взаимно-двойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
. . .
Если хj ≠ 0, то соответствующее ограничение дв. задачи – строгое равенство.
. . .
Если запас i-ого ресурса израсходован не полностью, то уi = 0.
Теорема об оценках. Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений – неравенств прямой задачи на величину ∆f(Х): ∆f(Х) =∆biyi
Пример использования теорем и свойств двойственных оценок для анализа оптимальных решений. На станках трех видов С1,С2, С3 последовательно обрабатываются детали четырех видов D1, D2, D3, D4. Известно, сколько часов каждая деталь изготавливается на каждом станке, сколько времени может отработать каждый станок и какая прибыль может быть получена при продаже одной детали каждого вида. Данные для решения задачи содержатся в таблице.
Симплекс-методом найден оптимальный план задачи по критерию «максимум прибыли», предусматривающий выпуск трех деталей второго вида и одной детали третьего вида.
х1*= 0 х2*= 3 х3*= 1 х4*= 0 Дать экономико-математический анализ оптимального плана.
Решение. Обозначим хj – объем выпуска деталей j- ого вида (j = 1,2,3,4) и запишем математическую модель задачи по критерию «максимум прибыли»:
max (3х1 + 4х2 + 3х3 + х4) 2х1 + 4х2 + 8х4 ≤ 12 7х1 + 2х2 + 2х3 + 6х4 ≤ 8 5х1 + 8х2 + 4х3 + 3х4 ≤ 48 х1, х2, х3, х4 ≥ 0
Двойственная задача имеет вид: min (12y1 + 8y2 + 48y3) 2y1 + 7y2 + 5y3 ≥ 3 4y1 + 2y2 + 8y3 ≥4 2y2 + 4y3 ≥ 3 8y1 + 6y2 + 3y3 ≥ 1 y1, y2, y3, ≥ 0
Для нахождения оценок y1, y2, y3 используем вторую теорему двойственности. Для этого в ограничения прямой задачи подставим значения оптимального плана. 2*0 + 4*3 + 8*0 =12 7*0 + 2*3 + 2*1 + 6*0 = 8 5*0 + 8*3 + 4*1 + 3*0 = 28 < 48 Поскольку третье ограничение выполняется как строгое неравенство, то у3 = 0. Т.к. х2 > 0 и х3 > 0, то второе и третье ограничения двойственной задачи – строгие равенства: 4y1 + 2y2 + 8y3 = 4 2y2 + 4y3 = 3 Итак, для получения двойственных оценок имеем систему линейных уравнений: у*3 = 0 4y*1 + 2y*2 + 8y*3 = 4 2y*2 + 4y*3 = 3, т.е. у*1 = 0,25; у*2 = 1,5; у*3 = 0.
Вычислим значения целевых функций прямой и двойственной задачи: F (х*) = Z (у*) = 15. По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.
Экономико-математический анализ оптимальных решений базируется на свойствах двойственных оценок. В пределах устойчивости двойственных оценок имеют место следующие свойства. 1. Величина двойственной оценки того или иного ресурса показывает на сколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу. В рассматриваемом примере увеличение фонда времени работы станка С1 на 1 час привело бы к росту максимальной суммы прибыли на 0,25 у. е. (у*1 = 0,25), а увеличение фонда рабочего времени третьего станка не повлияет на оптимальный план выпуска продукции и сумму прибыли. 2. Двойственные оценки отражают сравнительную дефицитность различных ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем не дефицитны (избыточны). В нашем примере недефицитным ресурсом является фонд рабочего времени станка С3 поскольку у*3 = 0. Острее ощущается дефицитность ресурса С2 (у*2 = 1,5), он более дефицитен, чем ресурс С1 (у*1 = 0,25). 3. Двойственные оценки позволяют определять своеобразные «нормы заменяемости ресурсов»: имеются в виду не абсолютная заменяемость ресурсов, а относительная, т.е. заменяемость с точки зрения конечного эффекта и лишь в конкретных условиях данной задачи. В нашем примере относительная заменяемость ресурсов определяется соотношением 0,25: 1,5 = 1: 6. 4. С помощью двойственных оценок можно определять выгодность производства новых изделий: если Предположим в нашем примере следует решить вопрос о целесообразности включения в программу производство деталей нового (пятого) вида при затратах ресурсов станков: 8, 2 и 3 соответственно и ожидаемой удельной прибыли 6 у.е. ∆5 = 0,25 * 8 + 1,5 * 2 + 0 * 3 – 6 = - 1 < 0 – выгодно. План перевозок
Совокупность всех переменных х ij обозначим Х, тогда целевая функция задачи будет иметь вид:
а ограничения выглядят следующим образом:
хij > 0. Условия (*) означают полное удовлетворения спроса всех потребителей, условия (**) определяют полный вывоз продукции от всех поставщиков. Необходимым и достаточным условием разрешимости этой задачи является условие баланса:
Транспортная задача, в которой имеет место равенство (***), называется закрытой и может быть решена как ЗЛП симплексным методом. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения. Наиболее применяемым методом является метод потенциалов. Если баланс (***) не выполняется, то транспортная задача является открытой. Для решения открытой транспортной задачи методом потенциалов ее сводят к закрытой задаче путем ввода или фиктивного потребителя или фиктивного поставщика.
Пример решения открытой транспортной задачи методом потенциалов. Найти оптимальное распределение поставок для транспортной задачи.
Суммарная мощность поставщиков (190) < суммарного спроса потребителей (200) – следовательно, задача открытого типа. Для решения задачи методом потенциалов приведем ее к закрытому типу путем введения фиктивного поставщика. Для этого добавим в таблицу строку с нулевыми стоимостями и объемом поставщика 10 единиц.
Этап 1. Первоначальное закрепление потребителей за поставщиками. Рассмотрим два метода получения начального распределения: метод северо-западного угла и метод наименьших стоимостей. При каждом из эх методов при заполнении некоторой клетки, кроме последней, вычеркивается или только строка матрицы перевозок или только столбец. При заполнении последней клетки вычеркивается и столбец и строка. В методе северо-западного угла в первую очередь заполняется клетка, стоящая в верхнем левом (северо-западном) углу матрицы перевозок. Для нашей задачи начальное распределение данным методом выглядит так: Заполняется клетка (1;1) – «40» и вычеркивается первая строка; Заполняется клетка (2;1) –«5» и вычеркивается первый столбец; Заполняется клетка (2;2) –«35» и вычеркивается второй столбец; Заполняется клетка (2;3) – «20» и вычеркивается вторая строка; Заполняется клетка (3;3) - «35» и вычеркивается третий столбец; Заполняется клетка (3;4) – «55» и вычеркивается третья строка; Заполняется клетка (4;4) – «10» и вычеркивается четвертая строка и четвертый столбец.
Суммарные затраты на транспортные расходы при данном плане составят:
F (х) = 4*40 + 3*5 + 2*35 + 3*20 +5*35 +2*55 + 0*10 = 590
При использовании метода наименьших стоимостей отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок. Для нашей задачи порядок заполнения клеток следующий:
Т.к. последняя строка относится к фиктивному поставщику, заполним ее в последнюю очередь. Х12 = 35 Х34 = 65 Х13 = 5 Х21 = 45 Х23 = 15 Х33 = 25 Х43 = 10
Стоимость перевозки: F (х) = 480. Следовательно, данный план перевозок значительно ближе к оптимальному, чем план, составленный по методу северо-западного угла.
Этап 2. Проверка оптимальности полученного плана перевозок. Для каждой строки (для каждого поставщика) введем показатель ui (i = 1,2,…, m). Для каждого столбца (для каждого потребителя) введем показатель vj (j = 1,2,…, n). Эти показатели называются потенциалами. Их удобно интерпретировать: ui - как цену продукта в пункте поставщика и vj – как ценупродукта в пункте потребителя.
Цена продукта в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е. vj = ui + с ij (1) Потенциалы подбираются таким образом, чтобы для заполненной клетки (i,j) выполнялось равенство (1). В нашем примере для начального распределения по методу наименьших стоимостей 7 заполненных клеток (7 уравнений) и 8 неизвестных. Значение одного из неизвестных можно задавать произвольно (например, u1 = 0), значение остальных неизвестных вычислим.
Далее для всех клеток матрицы перевозок определяются их оценки, которые обозначим dij, по формуле: dij = (ui + с ij) - vj Условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок (т.е. если все оценки ≥ 0, то план оптимален). Оценки клеток удобно представить в виде матрицы Наличие отрицательных оценок свидетельствует о том, что данный план перевозок не оптимален.
Этап 3. Улучшение неоптимального плана перевозок. Чтобы улучшить неоптимальный план перевозок, выбирается клетка матрицы перевозок с отрицательной оценкой. Если таких клеток несколько, то выбирается клетка с наибольшей по модулю отрицательной оценкой. Для выбранной клетки (3;1)строится замкнутая линия – контур, начальная вершина которой лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках; при этом направления отдельных отрезков контура могут быть только горизонтальными и вертикальными. Вершиной контура, кроме первой, является занятая клетка, где отрезки контура образуют прямой угол. В вершинах контура расставляются поочередно знаки «+» и «-», начиная со знака «+» в выбранной свободной клетке. Далее осуществляется перераспределение поставок. Величина перераспределенной поставки определяется как наименьшая из величин поставок в вершинах контура со знаком «-». На эту величину увеличиваются поставки в вершинах со знаком «+» и уменьшаются поставки в вершинах со знаком «-».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 46; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.232 (0.245 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 х1+3х2 = 300
х1+3х2 = 300
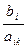 =
= 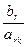 , где
, где 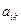 ≥ 0,
≥ 0,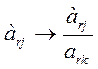
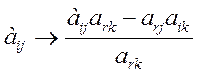
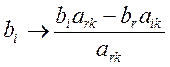
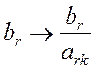
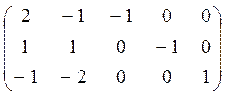
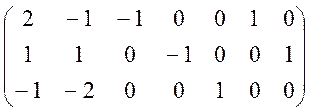
 -3х1 + 5х2 ≥ 1,
-3х1 + 5х2 ≥ 1,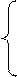 3х1 - 5х2 ≤ - 1,
3х1 - 5х2 ≤ - 1,

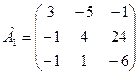



 А1` = -5 4 1 2
А1` = -5 4 1 2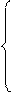 3у1 -у2 -у3 ≥ -7
3у1 -у2 -у3 ≥ -7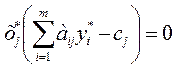
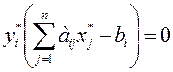
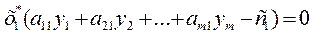
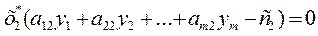
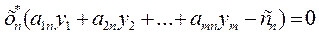
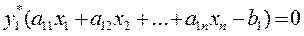
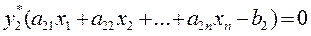
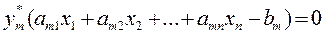

 ,
,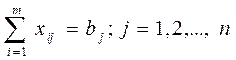 (*)
(*)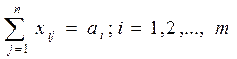 (**)
(**)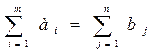 (***)
(***)