Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальные задачи линейного программированияСодержание книги
Поиск на нашем сайте
Экономико-математическая модель транспортной задачи Многие прикладные модели в экономике сводятся к задачам линейного программирования. Практически все задачи ЛП можно решить симплексным методом. Однако существуют более эффективные вычислительные процедуры решения некоторых типов задач ЛП. Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом. В m пунктах отправления А1,А2,…,А m , которые в дальнейшем будем называть поставщиками сосредоточено определенное количество единиц некоторого однородного продукта, которое обозначим а i (i = 1,2,…, m). Данный продукт потребляется в n – пунктах В1,В2,…,В n, которые будем называть потребителями; объем потребления обозначим bj (j = 1,2,…, n). Известны расходы на перевозку единицы продукта из пункта Аi в пункт Вj, которые равны с ij и приведены в матрице транспортных расходов:
Матрица транспортных расходов
Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь продукт вывозится из пунктов Аi в пункты Вj в соответствии с потребностью и общая величина транспортных издержек будет минимальной. Обозначим количество продукта, перевозимого из пункта Аi в пункт Вj через х ij. План перевозок
Совокупность всех переменных х ij обозначим Х, тогда целевая функция задачи будет иметь вид:
а ограничения выглядят следующим образом:
хij > 0. Условия (*) означают полное удовлетворения спроса всех потребителей, условия (**) определяют полный вывоз продукции от всех поставщиков. Необходимым и достаточным условием разрешимости этой задачи является условие баланса:
Транспортная задача, в которой имеет место равенство (***), называется закрытой и может быть решена как ЗЛП симплексным методом. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения. Наиболее применяемым методом является метод потенциалов. Если баланс (***) не выполняется, то транспортная задача является открытой. Для решения открытой транспортной задачи методом потенциалов ее сводят к закрытой задаче путем ввода или фиктивного потребителя или фиктивного поставщика.
Пример решения открытой транспортной задачи методом потенциалов. Найти оптимальное распределение поставок для транспортной задачи.
Суммарная мощность поставщиков (190) < суммарного спроса потребителей (200) – следовательно, задача открытого типа. Для решения задачи методом потенциалов приведем ее к закрытому типу путем введения фиктивного поставщика. Для этого добавим в таблицу строку с нулевыми стоимостями и объемом поставщика 10 единиц.
Этап 1. Первоначальное закрепление потребителей за поставщиками. Рассмотрим два метода получения начального распределения: метод северо-западного угла и метод наименьших стоимостей. При каждом из эх методов при заполнении некоторой клетки, кроме последней, вычеркивается или только строка матрицы перевозок или только столбец. При заполнении последней клетки вычеркивается и столбец и строка. В методе северо-западного угла в первую очередь заполняется клетка, стоящая в верхнем левом (северо-западном) углу матрицы перевозок. Для нашей задачи начальное распределение данным методом выглядит так: Заполняется клетка (1;1) – «40» и вычеркивается первая строка; Заполняется клетка (2;1) –«5» и вычеркивается первый столбец; Заполняется клетка (2;2) –«35» и вычеркивается второй столбец; Заполняется клетка (2;3) – «20» и вычеркивается вторая строка; Заполняется клетка (3;3) - «35» и вычеркивается третий столбец; Заполняется клетка (3;4) – «55» и вычеркивается третья строка; Заполняется клетка (4;4) – «10» и вычеркивается четвертая строка и четвертый столбец.
Суммарные затраты на транспортные расходы при данном плане составят:
F (х) = 4*40 + 3*5 + 2*35 + 3*20 +5*35 +2*55 + 0*10 = 590
При использовании метода наименьших стоимостей отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок. Для нашей задачи порядок заполнения клеток следующий:
Т.к. последняя строка относится к фиктивному поставщику, заполним ее в последнюю очередь. Х12 = 35 Х34 = 65 Х13 = 5 Х21 = 45 Х23 = 15 Х33 = 25 Х43 = 10
Стоимость перевозки: F (х) = 480. Следовательно, данный план перевозок значительно ближе к оптимальному, чем план, составленный по методу северо-западного угла.
Этап 2. Проверка оптимальности полученного плана перевозок. Для каждой строки (для каждого поставщика) введем показатель ui (i = 1,2,…, m). Для каждого столбца (для каждого потребителя) введем показатель vj (j = 1,2,…, n). Эти показатели называются потенциалами. Их удобно интерпретировать: ui - как цену продукта в пункте поставщика и vj – как ценупродукта в пункте потребителя.
Цена продукта в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е. vj = ui + с ij (1) Потенциалы подбираются таким образом, чтобы для заполненной клетки (i,j) выполнялось равенство (1). В нашем примере для начального распределения по методу наименьших стоимостей 7 заполненных клеток (7 уравнений) и 8 неизвестных. Значение одного из неизвестных можно задавать произвольно (например, u1 = 0), значение остальных неизвестных вычислим.
Далее для всех клеток матрицы перевозок определяются их оценки, которые обозначим dij, по формуле: dij = (ui + с ij) - vj Условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок (т.е. если все оценки ≥ 0, то план оптимален). Оценки клеток удобно представить в виде матрицы Наличие отрицательных оценок свидетельствует о том, что данный план перевозок не оптимален.
Этап 3. Улучшение неоптимального плана перевозок. Чтобы улучшить неоптимальный план перевозок, выбирается клетка матрицы перевозок с отрицательной оценкой. Если таких клеток несколько, то выбирается клетка с наибольшей по модулю отрицательной оценкой. Для выбранной клетки (3;1)строится замкнутая линия – контур, начальная вершина которой лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках; при этом направления отдельных отрезков контура могут быть только горизонтальными и вертикальными. Вершиной контура, кроме первой, является занятая клетка, где отрезки контура образуют прямой угол. В вершинах контура расставляются поочередно знаки «+» и «-», начиная со знака «+» в выбранной свободной клетке. Далее осуществляется перераспределение поставок. Величина перераспределенной поставки определяется как наименьшая из величин поставок в вершинах контура со знаком «-». На эту величину увеличиваются поставки в вершинах со знаком «+» и уменьшаются поставки в вершинах со знаком «-».
Производим перераспределение поставок.
Стоимость перевозок уменьшилась: 1*35+2*5+3*20+3*40+4*25+2*65+0*10 = 455 (была 480) Проверяем полученный план на оптимальность, т.е. переходим опять ко 2-ому этапу.
Матрица оценок
Т.к. все оценки ≥ 0, то полученный план является оптимальным. Заметим, что нулевая оценка свободной клетки (2;2) означает, что план не единственен.
Методы решения транспортной задачи могут применяться для решения задач, не имеющих ничего общего с перевозкой грузов. Например, это задача оптимального закрепления за станками операций по обработке деталей, или задача оптимального назначения и т.д.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.006 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
,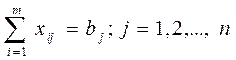 (*)
(*)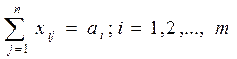 (**)
(**)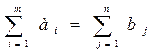 (***)
(***)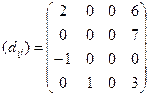

 3 +
45
3 +
45
 3 -
15
3 -
15