
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задач линейного программирования.
Наиболее простым и наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными. Графический метод решения ЗЛП состоит из следующих этапов: 1. Сначала строится многоугольная область допустимых решений (ОДР), соответствующая ограничениям. 2. Далее строится вектор–градиент линейной формы в какой-нибудь точке х0, принадлежащей допустимой области 3. Строится прямая 4. Находятся координаты предельной точки. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение
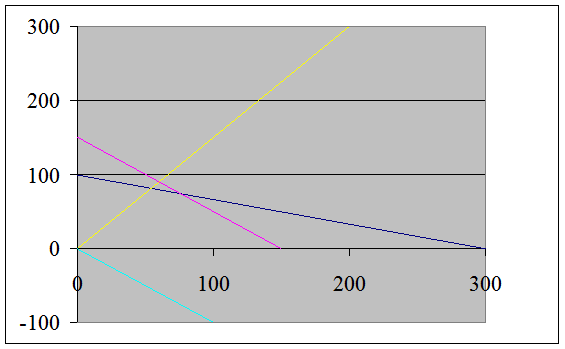
Пример. Решить графическим методом следующую ЗЛП: f(х1,х2) = (2х1+3х2) → max х1+3х2 £ 300 х1+х2 £ 150 х1,2 ³ 0 Прямые ограничения означают, что область решений будет лежать в первой четверти Декартовой системы координат. Этап 1. Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой х1+3х2 =300. Построим прямую по двум точкам (0;100) и (300;0). Множество решений строгого неравенства – одна из полуплоскостей, на которую делит плоскость построенная прямая. Какая из них является искомой, можно выяснить при помощи одной контрольной точки. Если в произвольно взятой точке, не принадлежащей прямой, неравенство выполняется, то оно выполняется и во всех точках той полуплоскости, которой принадлежит контрольная точка, и не выполняется во всех точках другой полуплоскости. В качестве контрольной точки удобно брать начало координат. Подставим значение координат (0;0) в неравенство, получим 0<300, т.е. оно выполняется. Следовательно, областью решения неравенства служит нижняя полуплоскость.
Аналогичным образом построим ОДР второго неравенства. х1+х2 = 150 Точки (0;150) и (150;0). х1+х2 < 150, при х1 = х2 = 0 неравенство 0 < 150 выполняется, область решения – нижняя полуплоскость. Заштрихуем общую область для всех неравенств, обозначим вершины многоугольника латинскими буквами А, В, С.
Этап 2. Для определения направления движения к оптимуму построим вектор-градиент, соединив его вершину ∆(100;150) с началом координат О (0;0). Этап 3. Построим прямую (линию уровня), перпендикулярную вектору-градиенту. Будем передвигать линию уровня до ее пересечения с точкой В. Далее она выходит из ОДР. Следовательно, именно в этой точке достигается максимум целевой функции. Этап 4. Координаты точки В найдем, решив систему из двух уравнений:
х1+х2 = 150 х1 = 75 х2 = 75 Координаты точки А (0;100) и точки С (150,0).
Т.к. координаты точки В равны х1 = 75 и х2 = 75, то максимум ЦФ равен 375.
      
|
|||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.168.56 (0.004 с.) |
 . Координаты вектора можно пропорционально увеличивать или уменьшать, при этом направление вектора не изменяется.
. Координаты вектора можно пропорционально увеличивать или уменьшать, при этом направление вектора не изменяется. , перпендикулярная вектору-градиенту, и передвигается в направлении этого вектора в случае максимизации
, перпендикулярная вектору-градиенту, и передвигается в направлении этого вектора в случае максимизации 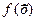 до тех пор, пока не покинет пределов многоугольной области. В случае минимизации целевой функции, прямую передвигают в направлении противоположном вектору-градиенту. Предельная точка (или точки) области при этом движении и является точкой максимума (минимума)
до тех пор, пока не покинет пределов многоугольной области. В случае минимизации целевой функции, прямую передвигают в направлении противоположном вектору-градиенту. Предельная точка (или точки) области при этом движении и является точкой максимума (минимума)  х1+3х2 = 300
х1+3х2 = 300



