Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особые случаи приведенной задачи.Содержание книги
Поиск на нашем сайте
1.Если матрица оценок (Cij)mn не является квадратной, то в модели следует записать ограничение:
2 Если некоторое назначение является недопустимым (в транспортной задаче – невозможна перевозка), то соответствующий элемент матрицы принимается в случае поиска максимума – равным (-М), в случае поиска минимума равным М. (М достаточно большое число). Задача нелинейного программирования формулируется так же, как и общая задача оптимального программирования, но со следующими требованиями: целевая функция f(х1,х2,…,хn) и (или) одна из функций gi(х1,х2,…,хn) являются нелинейными: Min (max) f (х1,х2,…,хn), gi(х1,х2,…,хn) { ≤,=,≥} bi, i=1,…, m, хj ≥ 0, j=1,…,n.
Задачи НЛП несравнимо сложнее ЛП и для них не существует универсального метода их решения (аналогично симплексному методу). Есть целый ряд методов решения НЛП: метод Лагранжа, градиентный метод, метод штрафных функций, метод динамического программирования. Градиентный метод - представляет собой итеративную (итерация - повторное применение какой-либо математической операции) процедуру, в которой переходят шаг за шагом от одного допустимого решения к другому так, что значение целевой функции улучшается. Однако в отличие от симплексного метода в нем не используется переход от одной вершины к другой. Для получения решения обычно требуется бесконечное число итераций. Метод штрафных функций аппроксимирует (заменяет) задачу с ограничениями задачей без ограничений с функцией, которая налагает штраф за выход из допустимой области. Метод динамического программирования. При решении задачи этим методом процесс решения делится на этапы, решаемые последовательно во времени.
Метод оптимизации Лагранжа Метод оптимизации Лагранжа или метод разрешающих множителей применяют для решения задач типа: Найти max (min) f (x 1, x 2,…, xn) при ограничениях φ i (x 1, x 2,…, xn) = 0, i =1,…, m Предполагают, что функции f и φ i непрерывны вместе со своими частными производными. 1) Для решения задачи составляют вспомогательную функцию (функцию Лагранжа), которая в области допустимых решений достигает максимума для тех же значений переменных x 1, x 2,…, xn, что и целевая функция f:
F (x 1, x 2,…, xn, λ1, λ2,…, λ m) = f (x 1, x 2,…, xn) + Σ m i =1 λ i φ i (x 1, x 2,…, xn) 2) Находят частные производные этой функции по переменным x 1, x 2,…, xn и множителям Лагранжа λ i, приравнивают их к нулю и получают систему уравнений: Решают эту систему например методом Жордана-Гаусса.
3) Получают решение (x * 1, x * 2,…, x * n, λ*1, λ*2,…, λ * m) и точка с координатами (x*1,x*2,…,x*n) является точкой экстремума (т.е. точкой минимума или максимума функции f). 4) Проверяют максимум это или минимум, для чего находят значение функции Лагранжа в окрестности экстремальной точки. Если приращение функции ∆F = F(x+∆x) - F(x) отрицательно, то в данной точке достигается максимум. Пример. Найти экстремум функции f = х1х2 + х2х3 при ограничениях х1+х2 =2 х2+х3 =2 Решение: Составляем функцию Лагранжа F (x 1, x 2, x 3, λ1, λ2) = х1х2 + х2х3 + λ1( х1+х2 -2) + λ2( х2+х3 -2) Дифференцируем ее по переменным x 1, x 2, x 3, λ1, λ2 и полученные выражения приравниваем к нулю.
Решив систему, получаем x*1 = x*2 = x*3 =1, f* = 2
Возьмем точку (0;2;0) из допустимой области, в ней f = 0, следовательно, точка (1;1;1) -точка глобального максимума.
Литература 1. Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании.-М.: Экономика, 1987. 2. Лопатников Л.И. Экономико-математический словарь.-М.:Наука, 1987. 3. Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В.Федосеева. – М.: ЮНИТИ, 1999. – 391 с. 4. Федосеев В.В. Экономико-математические методы и модели в маркетинге.-М.: Финстатинформ, 1996. 5. Экономико-математические методы и прикладные модели: Методические указания по выполнению контрольной работы, темы и задачи. Для студентов III курса по специальностям 060400 –«Финансы и кредит» и 060500 – «Бухгалтерский учет, анализ и аудит» /ВЗФЭИ.-М.:ВЗФЭИ, 2002.-104 с.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.107.181 (0.006 с.) |

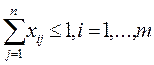 если работников > числа работ
если работников > числа работ 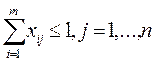 если работников < числа работ
если работников < числа работ 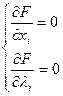 всего (n+m)- уравнений и (n+m)- неизвестных
всего (n+m)- уравнений и (n+m)- неизвестных