Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет логики и ее значениеСодержание книги
Поиск на нашем сайте
Л О Г И К А
(конспект лекций)
Минск БГЭУ 2016
ПРЕДИСЛОВИЕ
Изучение логики способствует повышению культуры мышления студентов. Логика учит человека сознательно применять законы и правильные формы мышления в своей умственной деятельности. Знание логики отражается и на профессиональной культуре человека. Принятию правильных решений в экономической деятельности и в сфере ее правового регулирования неизбежно должен предшествовать глубокий теоретический анализ хозяйственной ситуации. А это, в свою очередь, предполагает, наряду со специальными знаниями, также и умение мыслить логично, точно и последовательно, не допускать противоречий в рассуждениях, уметь вскрывать логические ошибки своих оппонентов. Высокая культура мышления повышает авторитет руководителя и доверие к нему как со стороны подчиненных, так и со стороны партнеров, что, безусловно, благоприятно сказывается на трудовой дисциплине в коллективе, на развитии деловых отношений и экономических связей предприятия. При изучении логики необходимо исходить из того, что усвоение теоретического материала не является самоцелью. Необходимо научиться применять логические законы, приемы и операции на практике, в процессе рассуждений. В достижении этой цели важную роль играют упражнения и решение логических задач. Поэтому значительную часть объема пособия занимают практические задания. Выполнение их поможет студентам активно усвоить курс логики и тем самым повысить культуру мышления, развить свой интеллектуальный потенциал и применить полученные знания в практической деятельности.
ПРЕДМЕТ ЛОГИКИ И ЕЕ ЗНАЧЕНИЕ
Что изучает логика?
Термин "логика", происходящий от древнегреческого logos (мысль, слово, понятие, разум, рассуждение, закон), употребляется в трех основных значениях. Во-первых, для обозначения определенных взаимосвязей явлений, событий, человеческих действий, для обозначения закономерностей объективного мира. Имея в виду это значение, можно, например, сказать "логика событий", «логика вещей», "логика исторического процесса", "логика экономического развития страны" и т.п. Во-вторых, этим словом обозначают законы, которым подчиняется наше мышление. Следование этим законам проявляется как последовательность, стройность, обоснованность мыслей, как убедительность рассуждений. Оценивая чьи-то рассуждения фразами "логично" или "нелогично", "железная логика", "женская логика", "в его словах нет никакой логики", мы используем термин "логика" именно в этом значении. И, в-третьих, логикой называют науку, изучающую мышление. Следует подчеркнуть, что логикой называют не только всю эту науку, но и ее отдельные разделы: символическая логика, логика предикатов, логика высказываний, многозначная логика, модальная логика и др. Объектом, который изучает логика, является мышление. Однако ограничиться констатацией этого факта нельзя, так как мышление изучается различными дисциплинами: философией, психологией, педагогикой, физиологией высшей нервной деятельности, психиатрией и др. Каждая из этих наук подходит к мышлению по-своему, выделяет в нем свой предмет исследования. А что именно интересует в мышлении логику, каков ее предмет? Предметом изучения логики являются формы мышления (отсюда и часто использующееся название науки - формальная логика). Следовательно, чтобы иметь ясное представление о логике как науке, необходимо разобраться в следующих вопросах: «Что такое формы мышления?», «Чем объясняется столь пристальное внимание к ним, приведшее к выделению самостоятельной отрасли научного знания?» Попытаемся разобраться в этих вопросах. Все сущее имеет как содержание, так и форму. Мышление в этом отношении не исключение. Содержание наших мыслей — это то, о чем мы думаем. Содержание наших мыслей может соответствовать действительности (в этом случае мы характеризуем мысль как истинную), либо не соответствовать (такая мысль будет ложной). Форма мысли — это определенный способ связи входящих в состав этой мысли элементов, способ их организации. Иными словами, различные соединения мыслей друг с другом называются логическими формами. С этих позиций наше мышление оценивается как правильное или неправильное. Для того чтобы наши рассуждения гарантированно приводили нас к истинным выводам, мы должны, осуществляя те или иные интеллектуальные операции, опираться на истинные исходные мысли. Если исходным пунктом наших рассуждений будут отдельные ложные мысли, то в итоге мы не можем быть уверенными в истинности выводов. Например: Все металлы — твердые тела. Ртуть не является твердым телом. Ртуть не является металлом. Ложность вывода в этом примере была предопределена ложностью первого исходного суждения. Итак, истинность исходных идей — необходимое условие гарантии истинности результатов наших рассуждений. Однако оказывается, что одной истинности мало. Само по себе это условие еще недостаточно. Вторым условием является правильность рассуждений. Что такое правильность мышления рассмотрим на следующем примере. Сравним два умозаключения: 1. Все экономические законы объективны. Закон соответствия спроса и предложения — экономический закон. Закон соответствия спроса и предложения — объективный закон.
2. Все экономические законы объективны. Закон соответствия спроса и предложения — объективный закон. Закон соответствия спроса и предложения — экономический закон. Оба умозаключения состоят из одних и тех же, и при этом истинных суждений. Они отличаются друг от друга лишь своим строением. Иначе говоря, одни и те же мысли в данных умозаключениях связаны друг с другом по-разному. Что же стоит за этим различием? Чтобы разобраться в этом, попробуем заменить во втором рассуждении понятие "закон соответствия спроса и предложения", допустим, на понятие "закон всемирного тяготения". При этой замене вторая посылка, так же как и первая, получится истинной: утверждение о том, что закон всемирного тяготения — объективный закон, соответствует действительности. А вот вывод из этих посылок получился ложным: данный закон не является экономическим законом. Схема (логическая форма), по которой осуществлялось второе рассуждение, не гарантировала при истинных исходных суждениях истинность заключения. Такие рассуждения называются неправильными. Что же касается первого рассуждения, то при любой замене понятия "закон соответствия спроса и предложения" в посылке (при условии, что в результате замены получится также истинное суждение) мы получим обязательно истинное заключение. Можно сказать, что схема, по которой осуществлялось первое рассуждение (независимо от его конкретного содержания), гарантирует при истинных посылках истинность заключения. Рассуждения, отвечающие этому требованию, называются правильными. Таким образом, одна из отличительных особенностей правильного рассуждения заключается в том, что от истинных посылок оно всегда ведет к истинному заключению. Теперь посмотрим на те же самые рассуждения с иной стороны. Согласившись с тем, что все экономические законы объективны, и что закон соответствия спроса и предложения — экономический закон, мы вынуждены принять и то, что закон соответствия спроса и предложения — объективный закон. Точно также, если мы приняли за истинное суждение "Все металлы — твердые тела" и учитываем, что ртуть не является твердым телом, то мы в силу необходимости, помимо нашей воли и желания, обязаны сделать вывод о том, что ртуть не является металлом. Мы как бы оказываемся во власти неизбежности. Наше мышление подчиняется некоей принудительной силе, его результаты во многом детерминированы и предопределены предшествующим знанием. Основоположник логики Аристотель называл эту особенность мышления "принудительной силой наших речей" и детерминированность мышления он сделал предметом специального исследования. В правильных рассуждениях выводы являются обоснованными, следуют с необходимостью, являются логичными. В подобных случаях говорят также, что между посылками и заключением имеет место отношение логического следования или, что заключение логически следует из посылок. А вот из посылок "Все экономические законы объективны" и "Закон соответствия спроса и предложения — объективный закон" вывод "Закон соответствия спроса и предложения — экономический закон" с необходимостью, с неизбежностью не вытекает. Такого рода рассуждения, где заключение может рассматриваться как истинное лишь с определенной степенью вероятности, называются неправильными. Правильность рассуждения определяется не содержанием наших рассуждений, а их формой. Это положение впервые было открыто древнегреческим философом Аристотелем: правильность рассуждения зависит только от формы этого рассуждения. Поскольку правильность мышления связана с формальными (структурными) аспектами мышления, логика отвлекается от содержательной стороны мышления, она концентрирует свое внимание на тех формах, в которых протекают различные мыслительные операции. Исследование логических форм безотносительно к их конкретному содержанию и составляет задачу логики как науки. Чтобы мышление было логичным, правильным, оно должно представлять не просто произвольную связь отдельных мыслей, а мысли должны связываться друг с другом по определенным логическим законам. Чтобы машина работала, детали ее должны быть соединены определенным образом. Так и элементы мышления. Логический закон указывает, как нужно соединять эти своего рода детали и употреблять их в процессе мышления. Логические законы касаются только способа соединения мыслей, но не их самих. Логический закон предполагает такую связь отдельных элементов мыслительного процесса, которая гарантирует переход от истинных посылок к истинному заключению. Правильность мысли означает вполне определенные (а не любые) связи между отдельными элементами этой мысли. Однако как определить, какая логическая форма является правильной, а какая связь между мыслями — нет? В большинстве случаев люди руководствуются так называемой интуитивной логикой. Но не всегда можно точно и однозначно решить этот вопрос исходя лишь из здравого смысла. Формальная логика выработала точные способы отделения правильных рассуждений от неправильных, наработала определенные стандарты, соответствие которым позволяет оценить мысль как правильную. Отделение правильных рассуждений от неправильных является основной задачей логики. Предметом логики является изучение стандартов корректности (правильности) разных рассуждений. Следование этим стандартам является обязательным условием успешного осуществления любой рациональной деятельности. Учитывая все это, можно определить логику следующим образом. Логика — это наука о формах мышления и приемах интеллектуальной познавательной деятельности, осуществляемой с помощью языка. Важным в понимании сути логики как науки является то, что она не занимается изучением того, как мыслит человек на самом деле, каковы особенности мышления у различных групп людей (возрастных, национальных, профессиональных и т.д.). Задача логики состоит в том, чтобы ответить на другой вопрос: как мы должны мыслить, если хотим достичь цели познавательного процесса – получить адекватные знания об исследуемых объектах?В связи с этим можно сказать, что логика носит нормативный характер. Она вырабатывает нормы, критерии, правильности осуществления интеллектуальных процедур, формируя тем самым некий канон, стандарт, идеал, следование которому является необходимым условием успешного осуществления научной и вообще любой рациональной деятельности. 1.2. Логическая форма
Рассмотрение понятия логической формы начнем с примеров. Возьмем следующие высказывания: "Все животные дышат воздухом", "Все металлы — электропроводные материалы", "Все расходы, связанные со сбытом и приобретением товаров, называются издержками обращения", "Все птицы летают", "Все реки впадают в моря". По своему содержанию эти утверждения совершенно различны. Более того, последние два не соответствуют действительности, т.е. являются ложными, остальные же — истинными. Но тем не менее все они имеют определенное сходство, которое заключается в построении данных высказываний. В каждом из них можно выделить в качестве структурного элемента ту часть, в которой представлено название (имя) предмета, о котором идет речь (животные; металлы; расходы, связанные со сбытом и приобретением товаров; птицы; реки). В другой части этих высказываний называются признаки, присущие указанным предметам (дышать воздухом, быть электропроводным материалом, называться издержками обращения, летать, впадать в моря). В каждом из высказываний присутствует слово "все", и подчеркивается различными средствами, что указанные признаки именно присущи тем предметам, о которых идет речь. Отвлекаясь от того, что и о чем говорится в данных суждениях, т.е. отвлекаясь от их содержания, мы обнаруживаем одинаковое строение данных высказываний. Наиболее полное отвлечение от смыслов и значений (т.е. от содержания) высказываний обеспечит нам использование символов. Обозначим ту часть высказываний, в которой содержится название предмета рассуждения, символом S (субъект), а часть, в которой содержится название признака, символом Р (предикат). Теперь строение всех сформулированных выше утверждений мы можем выразить следующей схемой: «Все S суть Р». Это и будет логическая форма данных утверждений. Теперь обратимся к более сложным в структурном отношении примерам: "Если возникают проблемы, связанные с валютой, то фирмы прибегают к бартерным сделкам", "Если воду нагреть до 100 ° С, то она закипит." "Если этот треугольник равносторонний, то он равнобедренный." В каждом из этих примеров содержится по два высказывания, соединенные союзом "если, то". Используя уже известный нам прием, отвлечемся от их содержательной стороны и заменим эти высказывания символами (допустим, первое из них обозначим буквой р, а второе — буквой q). В результате получим следующую схему: «Если р, то q». Это еще один пример логической формы. Теперь, основываясь на приведенных выше примерах, мы сможем сделать вывод, что логическая форма мысли — это структура, строение, определенный способ связи ее составных частей. Логическая форма — это та сторона мысли, которая не зависит от конкретного ее содержания, но служит способом связи ее содержательных частей. Совокупность процедур, при помощи которых мы абстрагируемся от содержательной стороны мышления, называется формализацией мышления. Выделенные после рассмотрения двух групп высказываний схемы (Все S суть Р, Если р, то q) являются примерами логических форм. Обратим внимание на следующее. Если в первой группе примеров при формализации мы раскрывали внутреннее строение высказываний и символами S и Р заменили конкретные имена (названия предметов и их свойств), то при формализации второй группы примеров символами р и q мы заменили уже целые высказывания. Соответственно можно сказать, что символы S и Р обозначают именные переменные, а символы р, q — пропозициональные переменные (от лат. пропозиция — высказывание). Кроме этих переменных, заменивших собою конкретное содержание мыслей, от которого мы и стремились отвлечься, в приведенных схемах представлены также логические термины "все", "суть", "если, то". Нетрудно заметить, что, независимо от конкретного содержания высказывания, эти термины сохраняют свое значение. Поэтому их еще называют логическими константами. В качестве таковых, кроме уже представленных, выступают слова "некоторые", "и", "или", "либо, либо", «следовательно», «неверно, что» и др. Для обозначения логических констант также используют символы, с которыми мы познакомимся позже. Итак, логическая форма может включать в себя пропозициональные, именные и прочие переменные. Кроме переменных для фиксации логических форм используют логические константы.
ПОНЯТИЕ Понятие как форма мышления
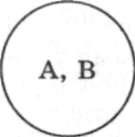
Понятие представляет собой одну из основных форм знания. Понятие – это простейший структурный элемент мышления. Эта структурная единица мышления лежит в основе всего нашего знания о мире. В понятиях фиксируются все знания, вырабатываемые человеком, это и обыденные, повседневные знания и знания научные. Каждая наука имеет свой понятийный аппарат. В химии, например, в него входят такие понятия, как «молекула», «вещество», «химическая реакция», «валентность», «оксиды» и т.д. В качестве примеров экономических понятий можно назвать такие понятия, как «стоимость», «рентабельность», «прибыль», «анализ хозяйственной деятельности», «аудит». В сфере юриспруденции широко используют понятия «правосознание», «дееспособность», «правонарушение», «преступление», «виновность», «умысел». Учитывая особое место понятий в мыслительной деятельности человека, последнюю иногда определяют как понятийное отражение действительности. В конечном счете мышление мы можем рассматривать как процесс оперирования понятиями. Понятия – это результат рационального отражения действительности человеком. В отличие от различных форм чувственного отражения (ощущение, восприятие, представление) понятие характеризуется высокой степенью абстрактности. Если формы чувственного познания (за исключением представления) возникают при непосредственном контакте с отражаемыми предметами, то понятийное отражение свободно от такой зависимости. Понятие абстрагировано от всех конкретных предметов. Например, в понятии «человек» мы отвлекаемся от конкретных индивидов, от наличия различных национальностей, рас и т.д. В понятиях мысленно выделяют предметы некоторого класса, исходя из того, что всем этим предметам присуща определенная совокупность признаков, отличающая их от других предметов. Если мы, например, сталкиваемся с понятием "отличник", то наше сознание сразу выделяет среди всех людей особую группу лиц, отраженных в данном понятии и обладающих следующими признаками: "учащийся", "имеющий по всем предметам отличные оценки". Мы часто употребляем выражения "иметь понятия о чем-либо", "не иметь ни малейшего понятия о чем-то" и т.п. Сказать, что человек имеет понятие о предметах какого-то класса мы можем лишь в том случае, когда человек знает о признаках, общих для предметов данного класса. Иметь понятие о чем-то – это значит знать, что представляет собой этот предмет, какие свойства ему присущи, в каких отношениях он находится с другими предметами. Само выделение предметов некоторого класса возможно на основе обобщения данных предметов по определенным признакам. Обобщение состоит в том, что мы отвлекаемся от всех индивидуальных и иных различий внутри класса. В результате предметы мыслятся абстрактно: только как обладающие указанной отличительной совокупностью признаков. Так в случае с понятием "отличник" отвлекаются (абстрагируются) от того, что есть отличники-школьники и отличники-студенты и т.д. В результате появляется относительно самостоятельное абстрактное образование — мысль о предмете, обладающем только отличительной совокупностью признаков. Однако, несмотря на обобщенный характер отражения предметов в понятиях, за абстрактными понятиями стоят в большинстве случаев конкретные предметы. Так, например, нет отличника вообще, а есть конкретные лица, обладающие соответствующими признаками. Понятия выражаются посредством отдельных слов или словосочетаний. Слова являются той материальной основой, без которой нельзя было бы ни вырабатывать понятия, ни оперировать ими. Однако об абсолютном тождестве понятия и слова говорить нельзя. Между ними нет однозначного соответствия. С одной стороны, одно и то же слово может выражать различные понятия. Например, «коса», «бор» (слова – омонимы). С другой стороны, одно и то же понятие может быть выражено разными словами (слова – синонимы). Взаимосвязь слова и понятия проявляется в том, что слово – это форма выражения понятия, а понятие выражает смысловое содержание слова. Понятие — это мысль, выражаемая словом или словосочетанием, в которой отражаются предметы того или иного класса посредством их обобщения и выделения по существенным отличительным признакам. Важнейшими характеристиками понятия являются содержание и объем. Содержание понятия — это совокупность признаков предметов, на основании которых предметы обобщаются в понятии. Признак — это любое свойство, любая характеристика предмета. Содержание понятия состоит из признаков, которые в своей совокупности присущи каждому предмету, отраженному в данном понятии, и только этим предметам. Некоторые авторы различают основное содержание и полное содержание понятия. Основное содержание характеризуется как совокупность только таких признаков, которых достаточно, чтобы отличить данные предметы от всех остальных. Такие признаки называют понятиеобразующими. Когда понятие рассматривается как некоторая система знаний об отраженных в нем предметах, то в этом случае употребим термин "полное содержание понятия". Полное содержание учитывает все знание, имеющееся о предметах, отраженных в понятии. Объемом понятия называется совокупность (класс) отраженных в нем предметов. Иначе говоря, если предмет обладает теми признаками, которые образуют содержание понятия, то он входит в объем данного понятия. Каждый из предметов, отраженных понятием, называется элементом его объема. Так, например, элементами объема понятия "областной центр Республики Беларусь" будут г. Гомель, Брест, Гродно, Могилев, Витебск, Минск. Существует несколько классификаций понятий. В каждой из них понятия подразделяют на виды на основании какого-то определенного признака. Так по объему понятия делят на общие, единичные и нулевые. Общим называется понятие, объем которого включает более одного элемента. Например, "книга", "студент", "стоимость", "религия". Если же объем понятия состоит лишь из одного элемента, то такое понятие будет единичным. Единичными являются такие понятия, как "первый президент Республики Беларусь", "Национальный банк Республики Беларусь". Пустые понятия в качестве объема имеют пустой класс, т.е. их объем равен нулю. Например, "вечный двигатель", "круглый квадрат", "родная дочь бездетной матери". Следует иметь в виду, что некоторые понятия с одной точки зрения могут быть расценены как пустые, и с другой — как имеющие объем. Например, понятие "Дед Мороз" с точки зрения его реального существования является пустым. Но как понятие, представляющее сказочный персонаж, оно пустым не является. В другой классификации понятия подразделяют на собирательные и несобирательные. Собирательными называют понятия, в которых группа однородных предметов мыслится как единое целое. Собирательными будут такие понятия, как "студенческая группа", "сервиз ", "созвездие ", "рота ", "лес ". Содержание собирательного понятия относится только к совокупности однородных предметов, но его нельзя отнести к каждому отдельному предмету, входящему в эту совокупность. Так, например, студенческая группа состоит из конкретных людей, но всякого отдельно взятого студента из этой группы нельзя отождествить со студенческой группой. Только взятые вместе, как одно единое целое, они образуют студенческую группу. Несобирательными называют такие понятия, содержание которых можно отнести к каждому отдельно взятому предмету, отраженному в этом понятии. Например, "студент группы № 1". Каждый конкретный человек, чья фамилия значится в списке этой группы, может сказать, что он является студентом группы № 1. Еще одна классификация подразделяет понятия на конкретные и абстрактные. Конкретными называют понятия, элементами объема которых являются отдельные предметы или классы предметов (как материальные, так и идеальные). Например, "операция", "материализм". Абстрактными называют понятия, обозначающие свойства предметов или отношения между предметами. Например, "справедливость", "дружба", "желтизна", "внимательность". Понятия делят также на отрицательные и положительные. Эта классификация основывается на том, что предметы могут быть охарактеризованы как обладающие определенными признаками, так и не обладающие какими-то иными признаками. Положительными являются понятия, указывающие на наличие у предмета того или иного свойства ("грамотный человек", "прилежный ученик", "жадность", "парнокопытные животные"). Отрицательными называют те понятия, которые обозначают, что указанное свойство отсутствует в предметах ("неграмотный человек", "невыдуманная история", "бескорыстный поступок"). Есть еще одна классификация, подразделяющая все понятия на относительные и безотносительные. Относительными называют понятия, содержание которых характеризует предмет по признакам-отношениям, т.е. по признакам, прямо указывающим на отношение к какому-то другому предмету. В относительных понятиях мыслятся предметы, существование одного из которых предполагает существование другого. Например, "сын", "сестра", "сосед", "супруг", "основание". (Мужчины рассматриваются в качестве сыновей по отношению к их родителям; "Анна — сестра Екатерины", "Иван — сосед Павла", "Иван Иванович — супруг Марии Ивановны", и т.д.) Б езотносительными являются понятия, содержание которых характеризует предмет по признакам — свойствам, которые есть (или отсутствуют) у предмета самого по себе, без всякого соотнесения с другими предметами. Например, "деревня", "город", "человек", "животное", "учебник". Различают также четкие и нечеткие понятия. Речь в данном случает идет о ясности, точности их содержания и о точности, четкости их объема. Если понятие характеризуется ясно, точно определенным содержанием и объемом и если относительно любого предмета можно однозначно решить, входит или не входит этот предмет в объем данного понятия, то это понятие называется четким. Например, понятие "прямоугольник". Оно характеризуется ясно, точно определенным содержанием и объемом. И относительно любой плоскостной геометрической фигуры мы со всей определенностью можем сказать, относится она к прямоугольникам (входит в объем данного понятия) или нет. Четкими будут и такие понятия, как "рентабельное предприятие", "студент-заочник", "совместное предприятие". Если же невозможно точно сказать, какие признаки составляют содержание понятия и какие объекты входят в его объем, то такое понятие следует считать нечетким (неопределенным, расплывчатым, размытым, неточным). Например, понятие "хороший шахматист". Неясно, каким конкретным критериям должен соответствовать человек, которого можно отнести к хорошим шахматистам. Неясно также, кого именно из шахматистов можно включить, а кого нельзя включить в эту группу. К числу нечетких относится большинство экономических понятий. . 2.2. Отношения между понятиями Рассуждая, человек совершает определенные действия с понятиями. Чтобы правильно оперировать понятиями, необходимо учитывать то обстоятельство, что понятия находятся в определенных отношениях между собой. Говорить об определенных отношениях мы можем только применительно к сравнимым понятиям. Понятия сравнимы между собой, если их содержания имеют хотя бы один общий признак, т.е. такие понятия можно отнести к общему для них классу. Например, понятия "университет" и "школа" относятся к учебным заведениям. Если же в содержании понятий нет ни одного общего признака, то такие понятия называются несравнимыми. Например, "экономические отношения" и "кислота". Строго говоря несравнимость — вещь довольно условная. В конечном счете любые понятия можно подвести под одно общее понятие, т.е. найти в предметах, отраженных в этих понятиях, какие-то общие черты. Таким образом о несравнимости мы говорим в тех случаях, когда сходство между предметами не имеет значения. Среди несравнимых понятий не существует никаких отношений. Отношения между сравнимыми понятиями подразделяют на отношения совместимости и отношения несовместимости. Понятия считаются совместимыми, если их объемы совпадают между собой либо полностью, либо частично, т.е. объемы этих понятий имеют общие элементы. Если же объемы понятий не имеют общих элементов, то такие понятия называются несовместимыми. Отношения между объемами понятий изображают при помощи специальных схем — кругов Эйлера, названных по имени Леонарда Эйлера (1707 - 1783) — швейцарского математика, физика и астронома. Выделяют три типа совместимости: равнообъемность (равнозначность), перекрещивание (пересечение), подчинение. Равнообъемными (равнозначными) считают такие понятия, которые имеют разное содержание, но объемы которых полностью совпадают. Например, "столица Республики Беларусь" (А) и "крупнейший промышленный центр Республики Беларусь" (В). Обратим внимание на то, что по содержанию это разные понятия, но объем у них один и тот же (рис. 2.1).
Рис. 2.1. Понятия А и В равнообъемны
П ерекрещивающимися являются понятия, имеющие в своих объемах некоторые общие элементы, т.е. объемы этих понятий частично (но не полностью) совпадают. Например, "отец" и "брат"; "преподаватель экономической теории" и "преподаватель БГЭУ"; "международные отношения” и "торговля" (рис. 2.2). ______________
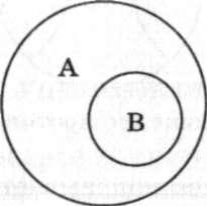
Отношение подчинения характеризуется тем, что объем одного понятия (подчиненного) полностью входит в объем другого (подчиняющего), но не исчерпывает его, становится лишь его частью. Например, "лиственное дерево" (А) и "береза" (В) (рис. 2.3).
Рис. 2.3. Отношение подчинения
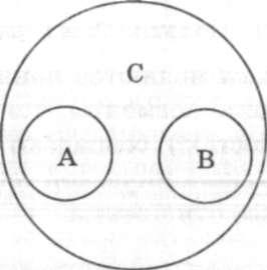
Если оба понятия, находящиеся в подобных отношениях, общие, то подчиняющее понятие называют еще родовым (родом), а подчиненное — видовым (видом). Отсюда еще одно название данного вида отношений — отношение рода и вида. Отношения несовместимости подразделяются на отношения соподчинения, отношения противоречия и отношения противоположности. В отношении соподчинения находятся такие понятия, которые являются видами одного рода, но объемы которых не имеют общих элементов. Например, понятия "тигр" (А) и "корова" (В) являются соподчиненными по отношению к понятию "животное"(С) (рис. 2.4).
Рис. 2.4. Отношение соподчинения
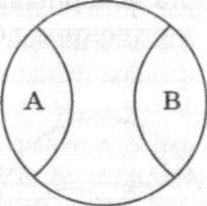
Противоположными (контрарными) называются понятия, содержащие признаки, которые находятся на разных полюсах определенной шкалы оценок. Противоположными являются, например, такие понятия, как храбрость" и "трусость"; "самый молодой преподаватель вуза" и "самый старый преподаватель вуза"; "богатый" и "бедный" (рис. 2.5).
Рис. 2.5. Отношение противоположности
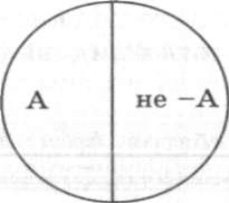
Данная схема наглядно показывает, что сумма объемов противоположных понятий не исчерпывает тот класс, видами которого они являются. Между этими крайними понятиями находятся еще определенные промежуточные понятия. Если обратиться к понятиям "самый молодой" и "самый старый", то мы видим, что между этими двумя крайностями можно расположить такие понятия, как "молодой", "человек среднего возраста", "пожилой", "старый". Не для всякого понятия можно подобрать противоположное понятие. Подобного рода отношения характерны прежде всего для понятий, выражающих оценочные характеристики. Попробуйте подобрать противоположное понятие, например, для таких понятий, как "стол", "дом" и т.п. Противоречащими (контрадикторными) называют такие два несовместимых понятия, одно из которых отрицает признаки, составляющие содержание другого. Например, "женатый" — "холостяк" ("неженатый").
Рис. 2.6. Отношение противоречия
Сумма объемов противоречащих понятий равна объему универсального класса, т.е. того родового понятия, в объеме которого они мыслятся. Оппозиция "храбрость" — "нехрабрость", например, исчерпывает все морально-волевые состояния человека в отличие от оппозиции "храбрость" — "трусость".
Деление понятий Деление понятия — это логическая операция, посредством которой объем делимого понятия (множество) распределяется на ряд подмножеств. В результате данной операции предметы, которые мыслятся в объеме исходного понятия, распределяются по группам. Например, углы в геометрии делят на острые, прямые и тупые. Эта операция имеет большое значение как для теоретической так и для практической деятельности человека. К ней прибегают, когда необходимо систематизировать какой-то материал, определить последовательность планируемых действий. В процессе выработки понятий происходит обобщение предметов того или иного класса, т.е. отражаются некие общие для предметов данного класса признаки и игнорируются их видовые и индивидуальные особенности. Но дальнейшее развитие соответствующих знаний предполагает конкретизацию, выявление особенного в общем. Все это и достигается посредством операции деления. В структуре операции деления различают: делимое понятие, члены деления, основание деления. Делимым называется родовое понятие, объем которого подвергается делению, т.е. в объеме которого выделяют различные виды. Члены деления — это видовые понятия, получившиеся в результате деления. Основание деления — это признак, с учетом которого проводится деление. Различают два вида деления понятия: деление по видоизменению признака и дихотомическое деление. Деление по видоизменению признака — это такое деление, при котором каждый из членов деления включает в свой объем предметы, обладающие одним и тем же признаком, служащим основанием деления, но этот признак у предметов, принадлежащих разным членам деления, находит свое особое проявление; предметам каждой группы, выделенной в результате деления, данный признак присущ в различной степе
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.119 (0.012 с.) |

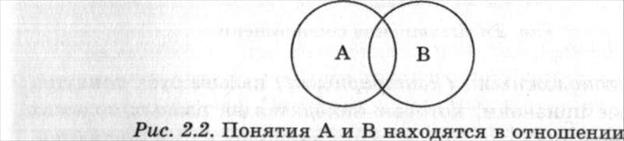
 перекрещивания
перекрещивания