
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переход от координатного способа к естественному:Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скоростью точки называется векторная величина, характеризующая быстроту и направление перемещения точки.
При векторном способе задания движения, вектор скорости:
Первая производная от радиус-вектора по времени (точка обозначает производную по времени);
Вектор, равный отношению вектора перемещения точки
При координатном способе задания движения
Проекции скорости:
Модуль скорости:
Направляющие косинусы:
Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
При естественном способе: – модуль скорости
вектор скорости из определения скорости точки
Если V > 0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот.
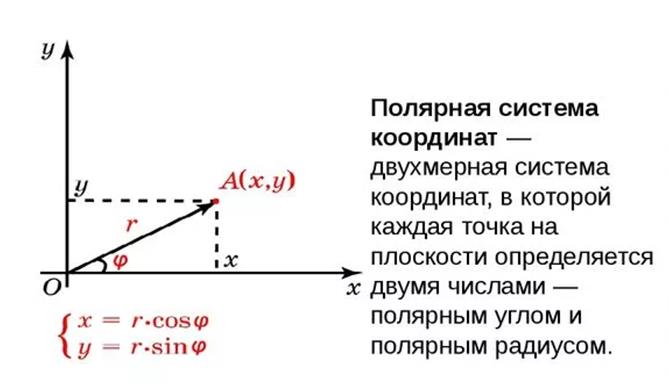
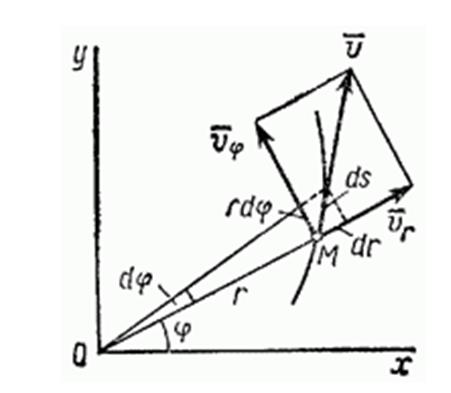
Движение в полярной системе координат: r = r(t) – полярный радиус, j = j(t) – угол.
Полярная система координат на плоскости задается точкой, которая называется полюсом, и лучом, который называется полярной осью. Координатами точки в полярной системе координат являются расстояние точки от полюса и угол между полярной осью и радиус-вектором этой точки. Этот угол называется полярным углом.
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси: x = r· cos j, y = r· sin j.
Проекции скорости на радиальное направление
Поперечное (трансверсальное) направление
модуль скорости
Ускорение точки
При векторном способе задания движения
При координатном способе задания движения
Проекции ускорения:
Так как
то
Модуль скорости:
Направляющие косинусы:
При задании движения в полярных координатах: проекции ускорения на радиальное направление
поперечное (трансверсальное) направление
модуль ускорения
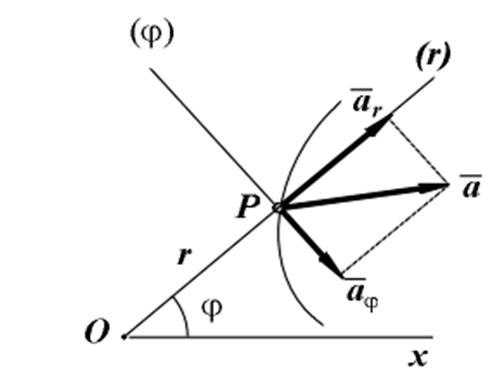
Радиальное и трансверсальное ускорения могут быть как положительными, так и отрицательными (на рисунке показан случай, когда радиальное ускорение положительное, а трансверсальное - отрицательное).
При естественным способе заданиядвижения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:
Из определения ускорения точки
определяется только свойствами траектории в окрестности данной точки, при этом
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 .
.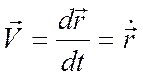
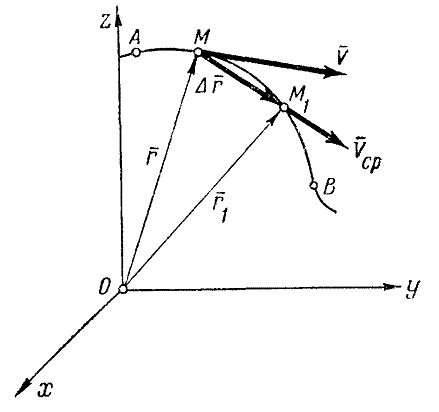
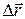 к промежутку времени
к промежутку времени 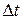 , называется средней скоростью за промежуток времени
, называется средней скоростью за промежуток времени 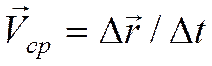 .
.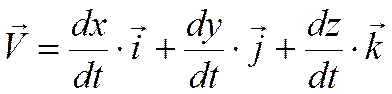 .
.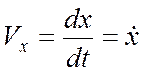 ,
, 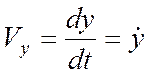 ,
, 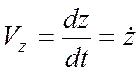 .
.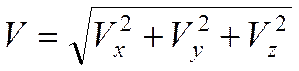 .
.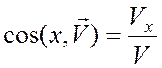 и т.д.
и т.д.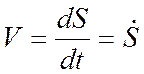 ,
,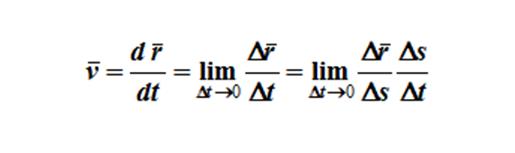

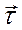 – орт касательной, т.е. скорость всегда направлена по касательной к траектории.
– орт касательной, т.е. скорость всегда направлена по касательной к траектории.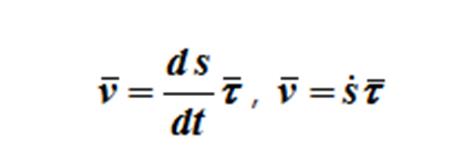
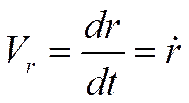 ,
,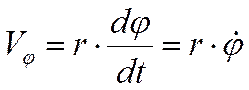 ,
,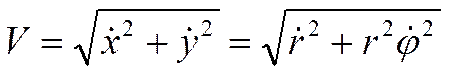 .
.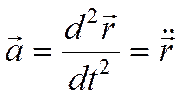 , [м/сек2].
, [м/сек2].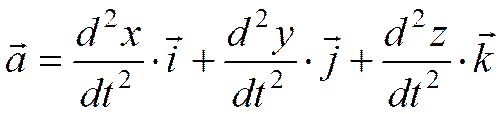 .
.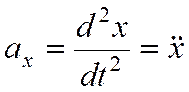 ,
, 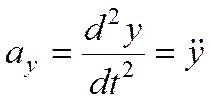 ,
, 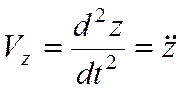 .
.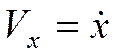 ,
, 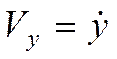 ,
, 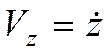 ,
,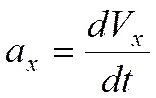 ,
, 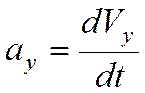 ,
, 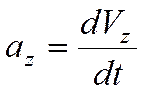
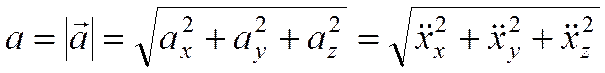 .
.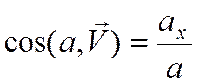 и т.д.
и т.д.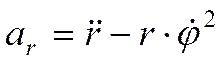 ,
,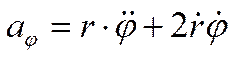 ,
,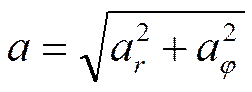 .
.
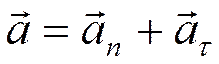 .
.





