Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для того чтобы полностью определить движение какого-либо твердого тела относительно выбранной системы отсчета, нужно знать движение каждой его точки относительно той же системы отсчета.Стр 1 из 9Следующая ⇒
КИНЕМАТИКА Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил.
В процессе исторического развития теоретической механики кинематические исследования долгое время (до XIX в.) не отделялись от вопросов динамики. Однако развитие техники машиностроения привело к необходимости выделения кинематики в особый раздел теоретической механики, и при этом кинематика стала теоретической основой теории механизмов и машин.
В теоретической механике изучается только механическое движение, т. е. происходящее с течением времени изменение положения одного тела по отношению к другому телу, с которым неизменно связана какая-нибудь система осей координат, называемая системой отсчета.
Систему отсчета можно связать с любым телом. Эта система может быть как условно неподвижной, так и движущейся.
Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к этой системе отсчета находится в покое.
Если же координаты точек тела с течением времени изменяются, то тело по отношению к выбранной системе отсчета находится в движении.
По отношению к различным системам отсчета точка или тело может совершать различные движения или находиться в покое. В этом смысле покой и движение точки или тела относительны и зависят от выбранной системы отсчета.
Для описания движения точки или тела нужно не только выбрать систему отсчета, но и установить способ определения времени, соответствующего тому или иному положению движущейся точки или движущегося тела в выбранной системе отсчета.
Время в теоретической механике считается универсальным (абсолютным), т. е. протекающим одинаково во всех рассматриваемых системах отсчета и не зависящим от движения одной системы по отношению к другой. При этом время рассматривается как непрерывно изменяющаяся скалярная величина t, играющая роль независимой переменной (аргумента).
Для измерения времени используются периодические процессы, данные природой (например, вращение Земли вокруг своей оси), либо периодические процессы, создаваемые искусственно (например, колебания маятника в маятниковых часах). За единицу времени обычно принимается одна секунда (1 сек).
Первоначально секунда была определена как интервал времени, 1/24·3600 части средних (за год) солнечных суток. Однако это определение секунды обладает существенным недостатком. Как показали наблюдения, суточное вращение Земли вокруг своей оси, на котором основано определение средних солнечных суток, подвержено колебаниям, закономерности которых пока еще не установлены и учету не поддаются. Возникшая в связи с этим неточность с определением секунды привела к необходимости искать другой эталон единицы времени, не связанный с суточным вращением Земли.
В международной системе единица времени одна секунда (1 сек) определена как интервал времени, равный 1/31556925,9747 части тропического года для 1900 г.
Это новое определение секунды устраняет погрешность прежнего определения. Но для современных научных и технических целей такое определение секунды все-таки не является достаточно точным. Поэтому в дальнейшем предполагается провести работы для создания еще более совершенного эталона времени на базе использования колебаний атомов и молекул.
Отсчет времени ведется от некоторого начального момента (t = 0), о выборе которого в каждом случае уславливаются. Всякий данный момент времени t определяется числом секунд, прошедших от начального до данного момента.
При этом момент времени считается положительным, если он следует за начальным, и отрицательным, если он предшествует начальному.
Число секунд, определяющих два каких-либо последовательных момента времени t 1 и t 2, называется промежутком времени (D t= t 2 – t 1 ).
Всякое твердое тело можно рассматривать как совокупность материальных точек. Разные точки движущегося тела могут совершать, различные движения относительно выбранной системы отсчета.
КИНЕМАТИКА ТОЧКИ
Естественный, Координатный, Векторный.
Векторный способ применятся главным образом при исследовании теоретических вопросов, а координатный и естественный употребляется преимущественно при решении различных практических задач.
Траектория точки – непрерывная кривая, которую описывает точка при своем движении.
Естественный способ указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: S = f (t) – закон движения точки. При прямолинейном движении: х = f (t).
Координатный способ положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x = f 1(t), y = f 2(t), z = f 3(t).
Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f (x,y) = 0 (для плоскости).
Векторный способ положение точки определяется ее радиус-вектором
Ускорение точки
При векторном способе задания движения
При координатном способе задания движения
Проекции ускорения:
Так как
то
Модуль скорости:
Направляющие косинусы:
При задании движения в полярных координатах: проекции ускорения на радиальное направление
поперечное (трансверсальное) направление
модуль ускорения
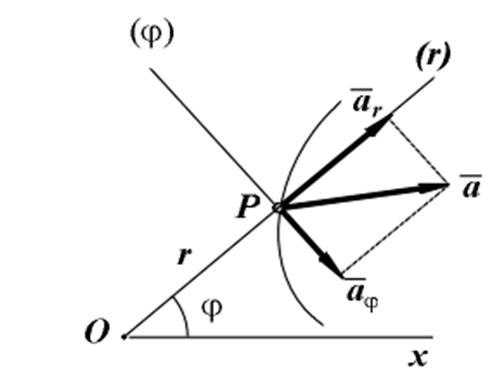
Радиальное и трансверсальное ускорения могут быть как положительными, так и отрицательными (на рисунке показан случай, когда радиальное ускорение положительное, а трансверсальное - отрицательное).
При естественным способе заданиядвижения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:
Из определения ускорения точки
определяется только свойствами траектории в окрестности данной точки, при этом
Угловое ускорение тела:
Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении.
Частные случаи вращения тела:
1) Равномерное вращение: w = const, j = w t, w = j / t,
2) Равнопеременное вращение: w = w 0 + e t; здесь начальный угол j0=0.
Скорости и ускорения точек вращающегося тела в векторнойформе.
Скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки:
Модуль векторного произведения:
V = w × r × sin (a)= w × (CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.
Формулы Эйлера:
где wx, wy, wz – проекции вектора угловой скорости.
Проекция вращательной (окружной) скорости: Vx = w y z – w z y; Vy = w z x – w x z; Vz = w x y – w y x.
Если ось вращения совпадает с осью z, то Vx = – w y; Vy = w x. Ускорение:
Касательное ускорение
Модуль полного ускорения:
Угол, между векторами полного и нормального ускорений:
ПЕРЕДАТОЧНЫЙ МЕХАНИЗМ
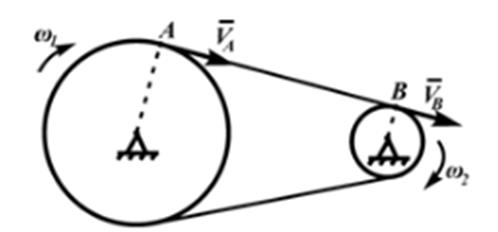
Цепная (ременная) передача
Скорости точек A и B цепи должны быть равны соответственно скоростям точек AB, принадлежащих шкивам:
VA = ω1∙ r1 = VB = ω2∙ r2, ω1 /ω2 = r2 /r1 ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
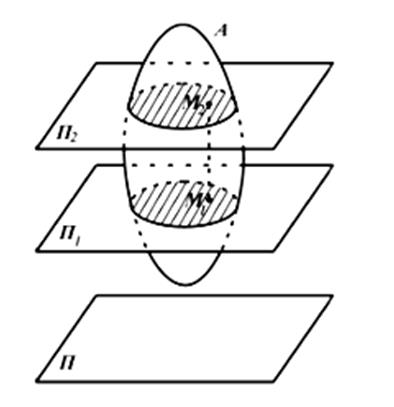
Плоскопараллельным движением твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости. При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например, M1M2) совершают одинаковые движения.
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.
Рассмотрим перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим вращательным движением на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B, с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например, AB), закон движения которого можно задать в виде:
xA= f1(t), yA= f2(t), j = f3(t), точка А называется полюсом.
Плоское движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А), и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.
СКОРОСТЬ ТОЧКИ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ
При движении фигуры в плоскости положение её точек можно определить соотношением (рисунок):
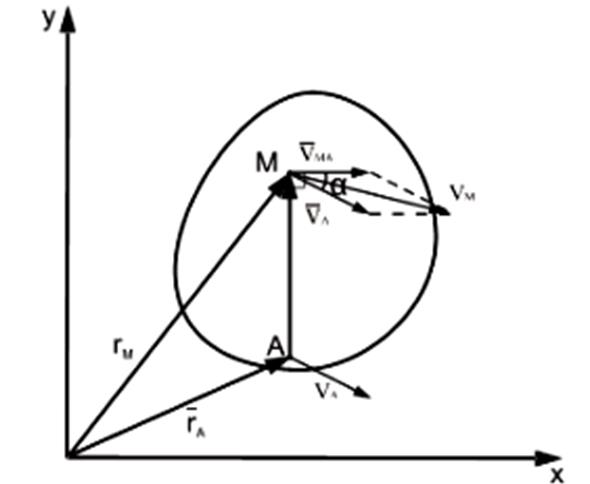
В данном случае точка A является полюсом.
МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
Теорема Эйлера-Шаля. Л юбое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
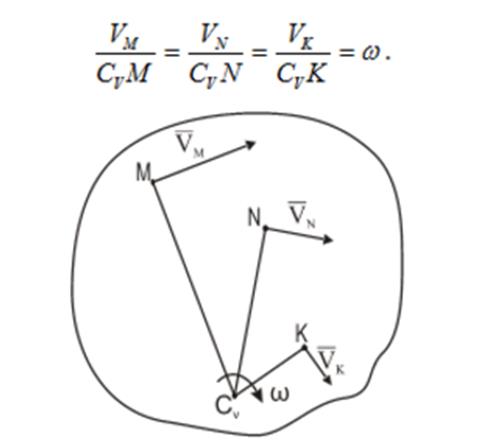
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.
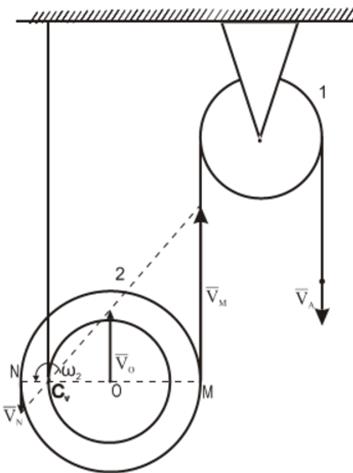
Из рис. ниже видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
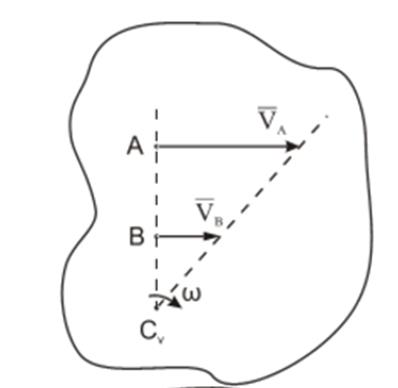
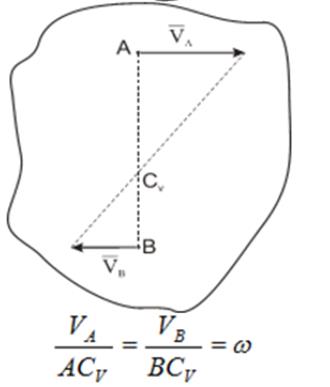
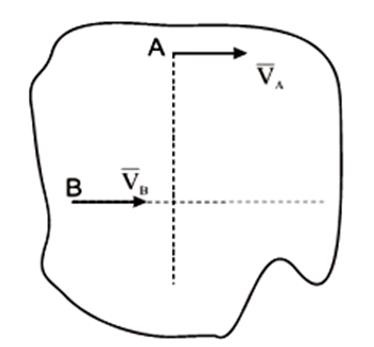
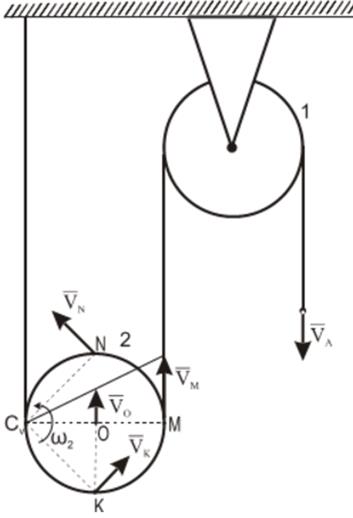
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.

здесь VB || VAВ, этом случае МЦС находится в “бесконечности”, т.е
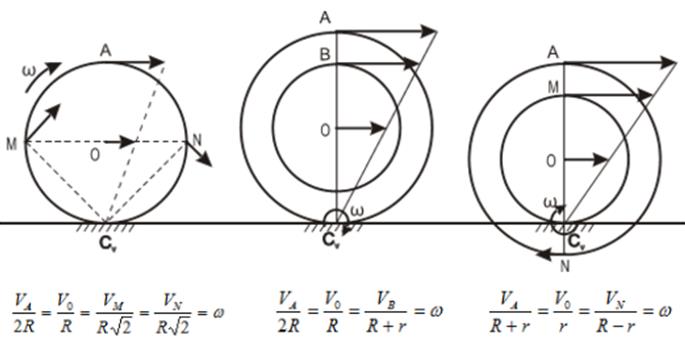
Формулы справедливы при отсутствии проскальзывания в точке СV.
При движении плоской фигуры МЦС непрерывно изменяет свое положение. Геометрическое место МЦС, отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место МЦС, отмеченных на плоскости фигуры, называется подвижной центроидой Пример. Колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность.
УСКОРЕНИЕ ТОЧЕК ПРИ ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ
Ускорения точек:
Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю.
Для его построения из точки А откладываем под углом a к ускорению аА отрезок AQ.
При этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорения, а векторы ускорений составляют с отрезками, соединяющими эти точки и мгновенного центра ускорения один и тот же угол
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
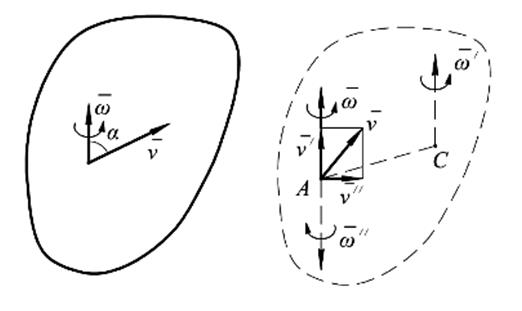
Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения. Пример сложного движения точки M.
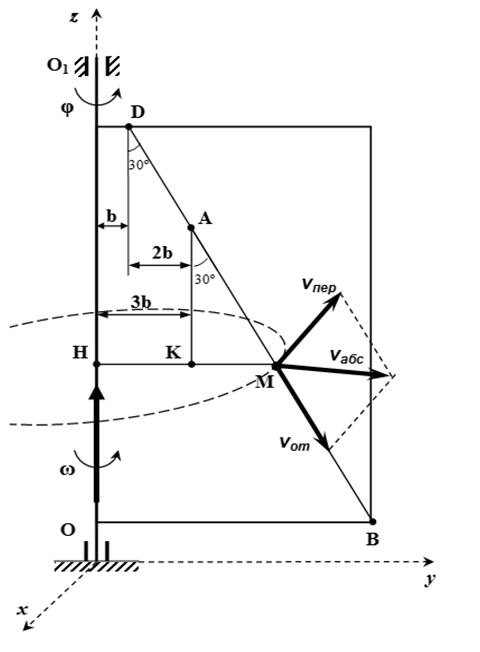
Квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка M. Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1 - по отношению к которой вращается квадрат и подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется точка M.
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом подвижной системы) является относительным - скорость в этом движении Vr.
Вращение точки M вместе с квадратом - переносное движение, скорость в этом движении - Ve. Абсолютное движение является результатом сложения переносного и относительного движений.
Переносная скорость:
поэтому абсолютная скорость точки равна геометрической сумме ее переносной (Ve) и относительной (Vr) скоростей
Модуль скорости:
ЗАДАЧА НА СЛОЖНОЕ ДВИЖЕНИЕ
Решение задачи
СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
Сферическим движением твердого тела называют такое движение, при котором одна точка тела остается все время неподвижной. Очевидно, траектории всех точек тела при таком движении располагаются на поверхностях сфер. Для определения положения тела с неподвижной точкой O в каждый момент времени свяжем две системы координат: неподвижную Ox1y1z1 и подвижную Oxyz, жестко связанную с телом, вращающимся вокруг точки O.
Положение подвижной системы координат относительно неподвижной однозначно определяется тремя углами, называемыми углами Эйлера: ψ — угол прецессии, θ — угол нутации φ — угол собственного вращения.
Линия пересечения подвижной плоскости xOy с неподвижной x1Oy1 называется линией узлов OK.
Угол прецессии определяет положение линии узлов на неподвижной плоскости x1Oy1. Для изменения этого угла тело должно вращаться вокруг оси Oz1, которую называют осью прецессии.
Угол нутации θ — это угол между осями Oz1 и Oz. При изменении угла происходит поворот тела вокруг линии узлов, которую также называют осью нутации.
Угол собственного вращения φ — это угол между линией узлов и подвижной осью Ox. При изменении угла φ тело вращается вокруг оси Oz (оси собственного вращения).
Для определения положения тела с одной неподвижной точкой в любой момент времени необходимо задать углы Эйлера как функции времени, т.е. уравнениями вращения твердого тела вокруг неподвижной точки
ψ = ψ(t), θ = θ(t), φ = φ(t).
Твердое тело, имеющее одну неподвижную точку, из одного положения в любое другое можно перевести одним поворотом вокруг некоторой оси, проходящей через неподвижную точку (теорема Эйлера-Даламбера).
Эту ось называют осью конечного вращения.
Ось, вокруг которой следует вращать тело, имеющее одну неподвижную точку, для перевода его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения (или мгновенной осью) для данного момента времени.
Мгновенная ось представляет собой геометрическое место точек тела, скорости которых в данный момент равны нулю.
Для того, чтобы определить положение мгновенной оси, достаточно найти какую-либо точку C твердого тела, скорость которой в данный момент равна нулю.
Тогда прямая, проходящая через точку C и неподвижную точку O, будет мгновенной осью вращения тела.
УГЛОВАЯ СКОРОСТЬ
Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.
Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω (рисунок).
Предел, к которому стремится отношение Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени
Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.
СФЕРИЧЕСКОМ ДВИЖЕНИИ
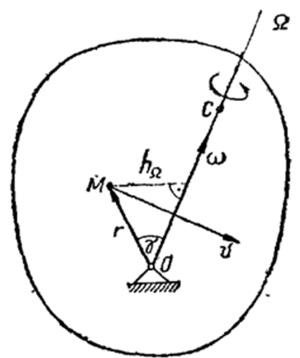
Скорости точек твердого тела, совершающего сферическое движение, в каждый момент времени определяются как их вращательные скорости при вращении вокруг мгновенной оси Ω (рисунок).
Зная положение мгновенной оси вращения Ω и угловую скорость тела ω, можно определить скорость любой точки тела M как скорость этой точки во вращательном движении вокруг мгновенной оси по известной формуле
ν = ω × r где r — радиус-вектор точки M, проведенный из неподвижной точки O.
Модуль скорости
ν = ωr sin γ = ωhΩ где hΩ — расстояние точки от мгновенной оси вращения.
Введем подвижную Oxyz и неподвижную Ox1y1z1 системы координат.
Для проекций скорости точки на неподвижные и подвижные оси получены формулы Эйлера:
для неподвижной системы координат
для подвижной системы координат
Из формул приведенных выше можно получить уравнения мгновенной оси в неподвижной и подвижной системах координат, положив для точек, лежащих на мгновенной оси, все проекции скорости равными нулю. Для неподвижной системы координат:
Модуль угловой скорости тела вокруг мгновенной оси
Через проекции на неподвижные оси координат:
Если положение мгновенной оси Ω уже установлено, то для нахождения угловой скорости ω достаточно знать скорость V какой-либо точки M, не лежащей на мгновенной оси.
Тогда, опустив из этой точки перпендикуляр hΩ на мгновенную ось Ω, получим ν = ω⋅ hΩ, откуда ω = ν / hΩ.
Для определения ускорения точки твердого тела служит теорема Ривальса: ускорение любой точки твердого тела при сферическом движении определяется как геометрическая сумма ее вращательного и осестремительного ускорений
a = a Eвр + a Ωос где
a Eвр = ε × r — вращательное ускорение точки, a Ωос = ω × ν — осестремительное ускорение точки. Модули этих ускорений
a Eвр = hEε и a Ωос = hΩω2 где hE — расстояние от точки до оси углового ускорения E, hΩ — расстояние от точки до мгновенной оси Ω.
Модуль ускорения точки можно найти как диагональ параллелограмма:
При сферическом движении осестремительное ускорение a Ωос направлено по перпендикуляру, опущенному из точки на мгновенную ось Ω, а вращательное ускорение a Eвр оказывается перпендикулярно плоскости проходящей через вектор углового ускорения ε и радиус-вектор r.
Направление вращательного ускорения не совпадает с направлением скорости.
Пара вращений
Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по модулю w 1 = w 2. Такая совокупность вращения называется парой вращений.
т.е.
Тогда мгновенный центр скоростей будет, находится в бесконечности и все точки тела в данный момент, будут иметь одинаковые скорости
Следовательно, результирующее движение тела будет поступательным (или мгновенно-поступательным) движением со скоростью V численно равной w 1 × АВ и направленной перпендикулярно плоскости, проходящей через векторы w 1 и w 2.
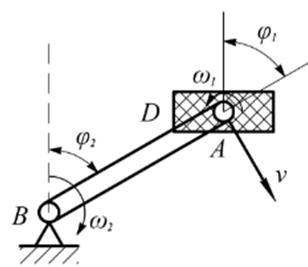
Примером такого движения является поступательное движение велосипедной педали относительно рамы велосипеда, являющееся результатом относительного вращения педали вокруг оси А, укрепленной на кривошипе ВА и переносного вращения кривошипа ВА вокруг оси В. Угловые скорости w 1 и w 2 в любой момент времени равны, так как j1 = j2.
Скорость поступательного движения педали
Сложение поступательного и Вращательного движений
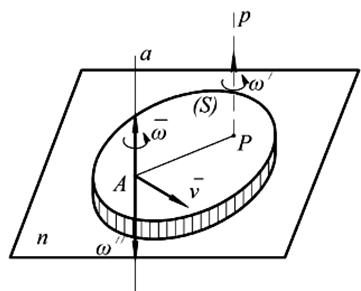
1. Скорость поступательного движения перпендикулярно к оси вращения ( Пусть сложное движение тела слагается из вращательного движения вокруг оси А а с угловой скоростью w и поступательного движения со скоростью
Если считать точку А полюсом, то рассматриваемое движение, как и всякое плоскопараллельное, будет действительно слагаться из поступательного со скоростью VA = V, т.е со скоростью полюса и вращательного вокруг оси Аа, проходящей через полюс. Вектор V можно заменить парой угловых скоростей
Векторы
Поворот тела вокруг осей Аа и Рр происходит с одной и той же угловой скоростью
2. Винтовое движение (
Сложное движение слагается из вращательного вокруг оси Аа с угловой скоростью Ось Аа называется осью винта.
Когда векторы
Расстояние, проходимое за время одного оборота любой точки, лежащей на оси винта, называется шагом h винта. Если величины
При постоянном шаге любая точка М тела, не лежащая на оси винта, описывает винтовую линию. Скорость точки М, находящейся от оси винта на расстоянии r, складывается из поступательной скорости Ve = V и перпендикулярной к ней скорости
Направлена скорость VM по касательной к винтовой линии.
3. Скорость поступательного движения
Сложное движение, совершаемое телом в этом случае, представляет собой общий случай движения свободного твердого тела.
Разложим вектор V на составляющие:
1)
2)
Скорость
Тогда у тела остается вращение с угловой скоростью
Проделанными операциями мы перешли от полюса А к полюсу С. Результат показывает, что в общем случае движения угловая скорость тела при перемене полюса не изменяется (
Поскольку при движении свободного твердого тела величины
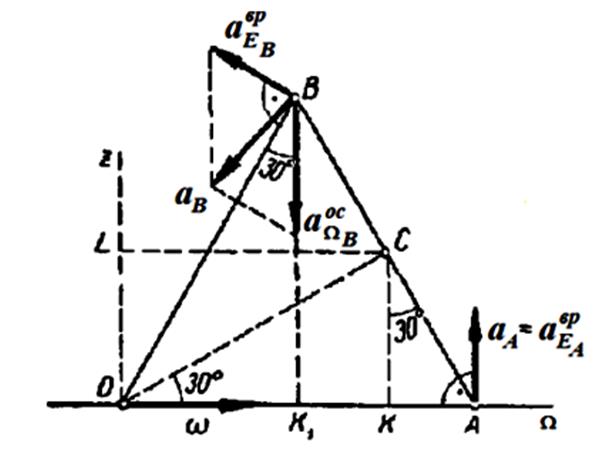
Решение.
1) Рассматриваемое движение конуса является сферическим, так как его вершина остается неподвижной. Так как конус катится по неподвижной плоскости, то образующая OA, которой он соприкасается с плоскостью, является мгновенной осью (все точки этой образующей имеют нулевую скорость). Зная скорость точки C, можно сразу определить угловую скорость конуса. Найдем расстояние от C до мгновенной оси:
Учитывая направление вектора νс, откладываем вектор ω от точки O вдоль мгновенной оси так, чтобы смотря ему навстречу, видеть вращение конуса происходящим против движения часовой стрелки;
2) для определения углового ускорения ε необходимо построить годограф угловой скорости ω. При качении конуса по горизонтальной плоскости вектор ω перемещается в этой плоскости, поворачиваясь вокруг вертикальной оси z. Так как модуль его не изменяется, то конец вектора ω описывает окружность в горизонтальной плоскости. Вектор ε геометрически равен скорости u конца вектора ω. В данном случае скорость u является вращательной вокруг оси z. Угловая скорость этого вращения ω1 определяется как угловая скорость вращения оси конуса OC вокруг оси z. Чтобы определить ее модуль, находим расстояние от точки C до оси z:
CL = OC cos30° = OA cos30° cos30° = 2r cos2 30° = = 40 ∙ 3/4 = 30 см.
Определяем ω1:
ω1= νс / CL = 60 / 30 = 2 с-1.
Скорость u находим как вращательную скорость точки – конца вектора угловой скорости ω при вращении вокруг оси z:
ε = u = ω1∙ω = 2∙2√3 = 6,93 с-2.
Вектор ε отложен от неподвижной точки в направлении скорости u, т.е. лежит в горизонтальной плоскости и перпендикулярен ω;
3) определим скорости
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.33.87 (0.359 с.) |

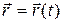 , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, называется годографом этого вектора. Т.е. траектория – годограф радиус-вектора.
, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, называется годографом этого вектора. Т.е. траектория – годограф радиус-вектора.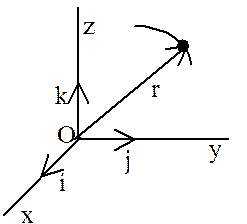
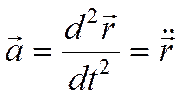 , [м/сек2].
, [м/сек2].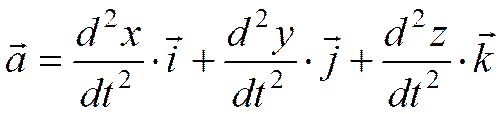 .
.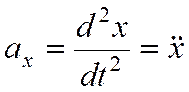 ,
, 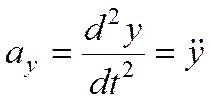 ,
, 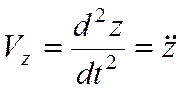 .
.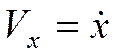 ,
, 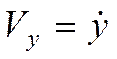 ,
, 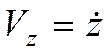 ,
,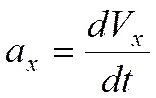 ,
, 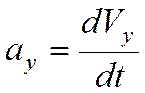 ,
, 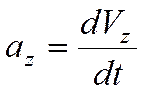
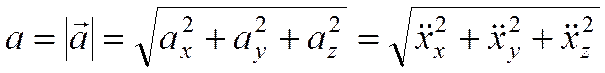 .
.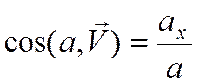 и т.д.
и т.д.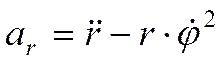 ,
,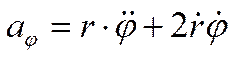 ,
,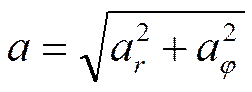 .
.
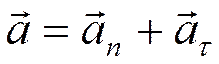 .
.


 , [рад/с2].
, [рад/с2].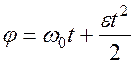 ,
,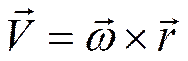

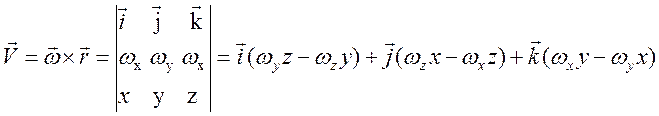 ,
,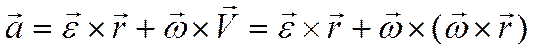 .
. ,
, .
.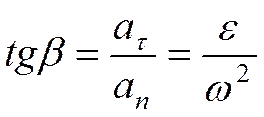 .
.

 .
.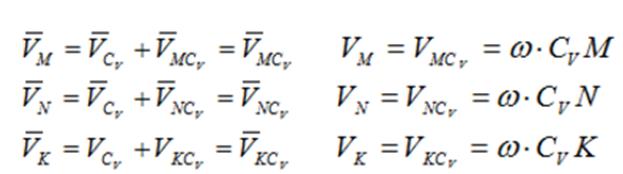


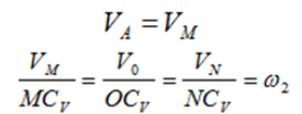
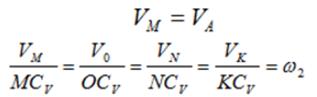
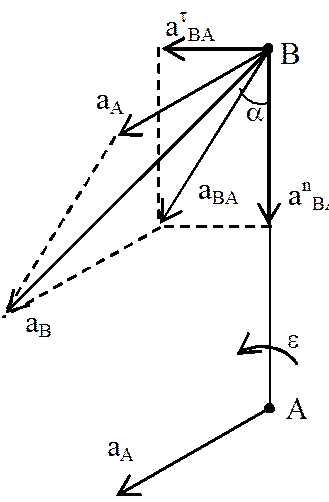
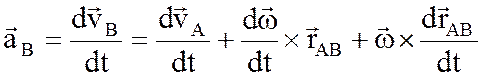 ,
, – ускорение любой точки (В) плоской фигуры геометрически складывается из ускорения полюса (А), центростремительного а n и касательного (тангенциального) а t ускорений во вращательном движении тела относительно полюса.
– ускорение любой точки (В) плоской фигуры геометрически складывается из ускорения полюса (А), центростремительного а n и касательного (тангенциального) а t ускорений во вращательном движении тела относительно полюса.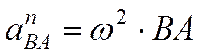 ,
, 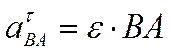 ,
,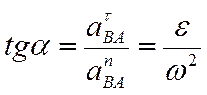 ,
, 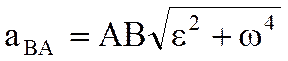 .
.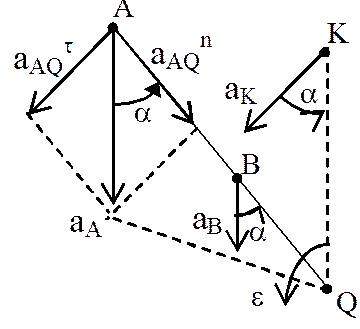
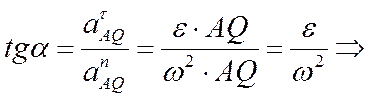

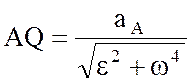 .
.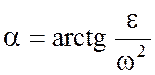 :
: 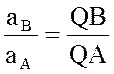 .
.
 ,
,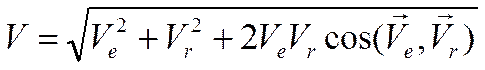 .
.







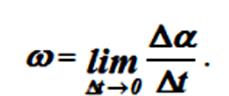
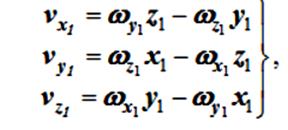
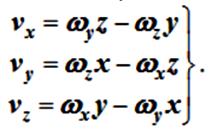
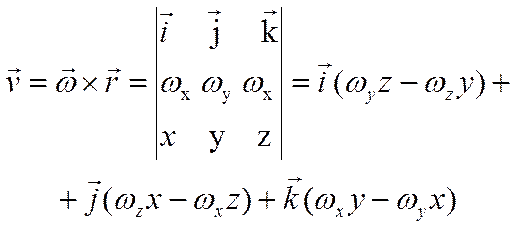

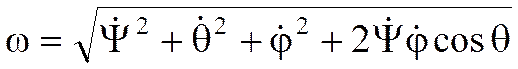
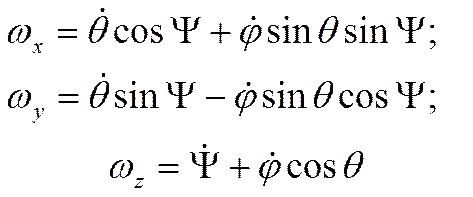

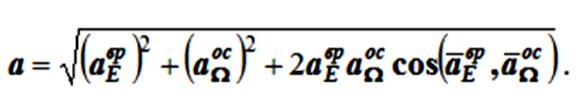

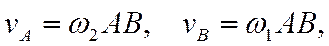
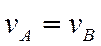
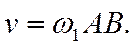
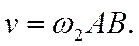
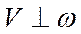 ).
).
 (пара вращений), беря
(пара вращений), беря 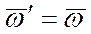 , а
, а 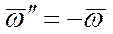 . При этом расстояние АР найдется из равенства
. При этом расстояние АР найдется из равенства 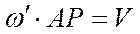
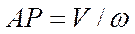
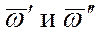 дают при сложении нуль, и мы получаем, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг оси Рр с угловой скоростью
дают при сложении нуль, и мы получаем, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг оси Рр с угловой скоростью 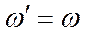 . Точка Р для сечения (S) тела является МЦС (
. Точка Р для сечения (S) тела является МЦС (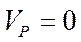 ).
).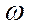 , т.е. вращательная часть движения не зависит от выбора полюса.
, т.е. вращательная часть движения не зависит от выбора полюса.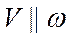 ).
).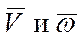 направлены в одну сторону, то винт будет правым; если в разные стороны – левым.
направлены в одну сторону, то винт будет правым; если в разные стороны – левым.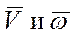 постоянны, то шаг винта также будет постоянным. Обозначая время одного оборота через Т, получим
постоянны, то шаг винта также будет постоянным. Обозначая время одного оборота через Т, получим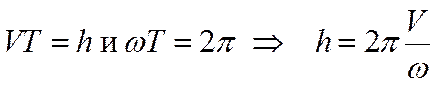

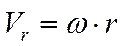 , получаемой во вращательном движении. Следовательно
, получаемой во вращательном движении. Следовательно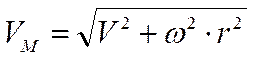
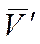 , направленную вдоль
, направленную вдоль 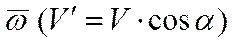 .
.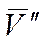 , перпендикулярную к
, перпендикулярную к 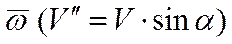 .
.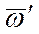 и
и 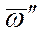 можно отбросить. расстояние АС найдем по формуле:
можно отбросить. расстояние АС найдем по формуле: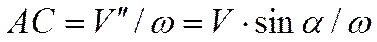 .
.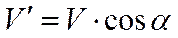 .
.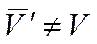 ).
). будут все время меняться и положение оси Сс, которую поэтому называют мгновенной винтовой осью.
будут все время меняться и положение оси Сс, которую поэтому называют мгновенной винтовой осью.