
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема О скоростях точек плоской фигуры
Скорость любой точки плоской фигуры при плоскопараллельном движении равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А. Вектор VMA=ω⋅ AM перпендикулярен отрезку АМ.
Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов
или спроецировать векторное равенство (1) на выбранные оси координат
Из теоремы о скоростях точек плоской фигуры следует, что проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны. Это легко показывается в рассуждениях:
так как VBA ⊥ AB, то и проекция VBA на ось АХ равна нулю. Следовательно, VBx = VAx

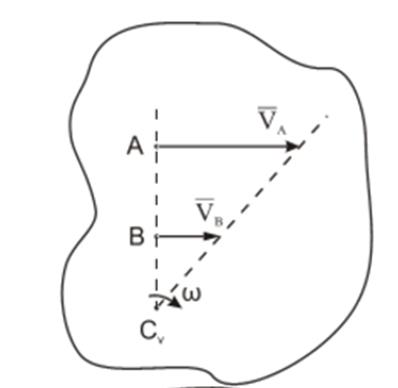
МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
Теорема Эйлера-Шаля. Л юбое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
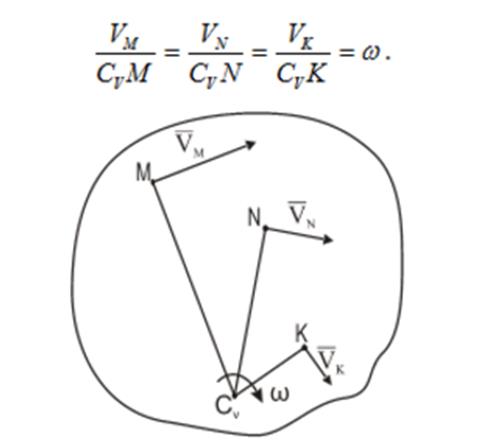
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.
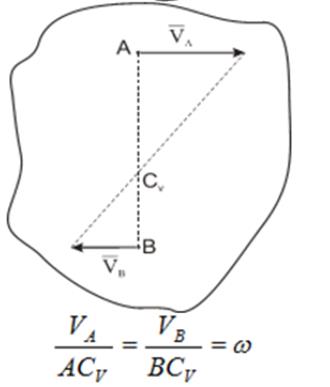
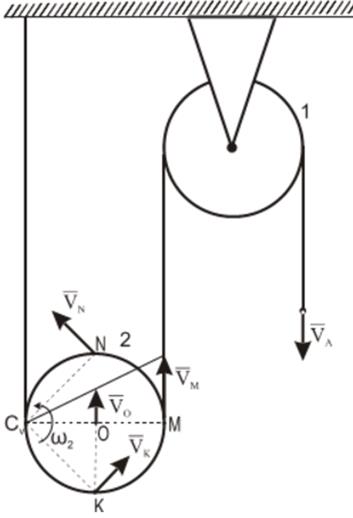
Из рис. ниже видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.

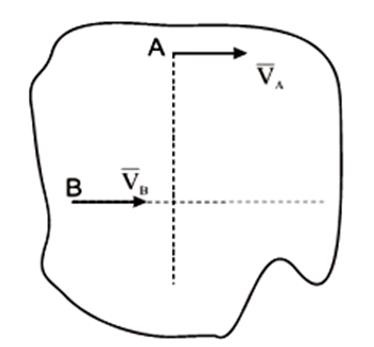
здесь VB || VAВ, этом случае МЦС находится в “бесконечности”, т.е
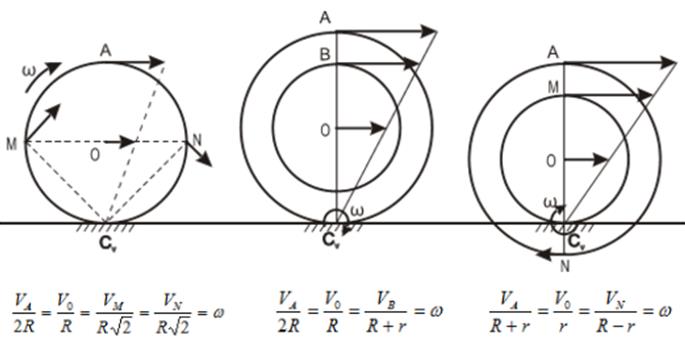
Формулы справедливы при отсутствии проскальзывания в точке СV.
При движении плоской фигуры МЦС непрерывно изменяет свое положение.
Геометрическое место МЦС, отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место МЦС, отмеченных на плоскости фигуры, называется подвижной центроидой Пример. Колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность.
Теорема Пуансо. При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде. УСКОРЕНИЕ ТОЧЕК ПРИ ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ
Ускорения точек:
Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю.
Для его построения из точки А откладываем под углом a к ускорению аА отрезок AQ.
При этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорения, а векторы ускорений составляют с отрезками, соединяющими эти точки и мгновенного центра ускорения один и тот же угол
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.217.134 (0.008 с.) |



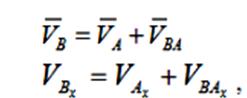
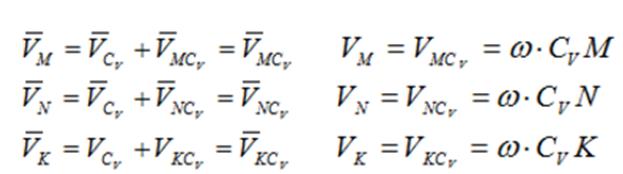


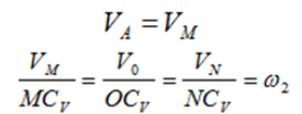
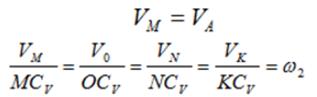
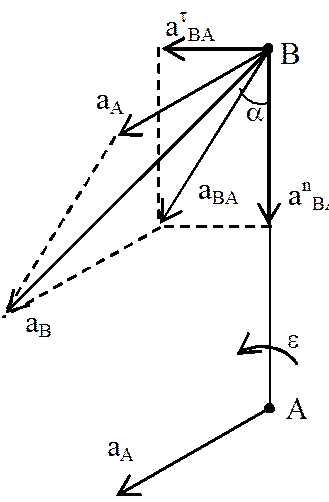
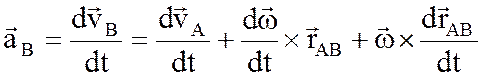 ,
, – ускорение любой точки (В) плоской фигуры геометрически складывается из ускорения полюса (А), центростремительного а n и касательного (тангенциального) а t ускорений во вращательном движении тела относительно полюса.
– ускорение любой точки (В) плоской фигуры геометрически складывается из ускорения полюса (А), центростремительного а n и касательного (тангенциального) а t ускорений во вращательном движении тела относительно полюса.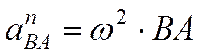 ,
, 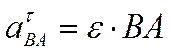 ,
,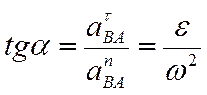 ,
, 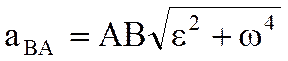 .
.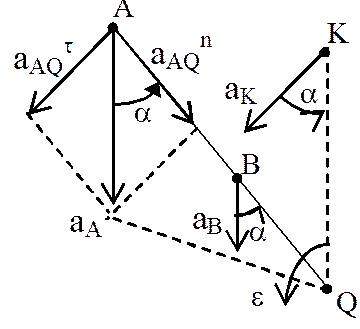
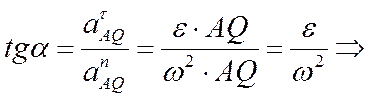

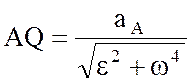 .
.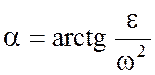 :
: 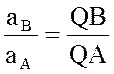 .
.


