Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест для учителей математикиСодержание книги
Поиск на нашем сайте
1. Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле. Вся работа заняла 12 часов. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал один из них, то работа заняла бы 20 часов. За какое время два комбайна могут убрать первое поле? - 18 - 12 - 9 - 6 2. Наибольшая длина отрезка, внутри которого не содержится ни одного корня данного уравнения - 5/4 π - π/4 - π/2 - 3/4 π 3. Уравнение x3-a=3x2 имеет три корня, если а принадлежит: - [-4;∞) - (-4;0) - (-∞;-4] - [-4;0] 4. Решение неравенства cosx≥b/2 принадлежит промежуткам [-π/3+2πn; π/3+2πn], n - b - b - b - b 5. Сумма остатков от деления числа 126450747 на 2, 3, 4, 5, 9, 10, 25 равна - 21 - 37 - 35 - 1524 6. Вычислить arcsin (sin10)-3p - 3p-10; - –10; - 10-3p; - другой ответ. 7. Найти площадь ромба АВСД, если радиусы окружностей, описанных около треугольников АВС и АВД равны соответственно 1 и 2. - 2, 50; - 2,65; - 2,48; - 2,56. 8. Разность между наибольшим и наименьшим значениями функции - 0,5 - 0,75 - - 9. Число
- 10 - 2 - 6 - 4 - 8 10. Сколько корней имеет уравнение: - 0; - 2; - 3; - 4. 11. Решением уравнения - - - - 12. Решением неравенства - (0; 1) U [2; +¥) - (0; 1] U [2; +¥) - [0; 1) U (2; +¥) - [0; 1] U [2; +¥) 13. Решите уравнение (х+1)4 + (х+3)4 = 706. Решением уравнения является - -6;2 - 6;2 - 6;-2 - -6;-2 14. Иррациональный корень уравнения - е; - - - 15. При каком положительном значении к наибольшее значение функции
- 15; - 5; - 9; - 25. 16. Производная функции у=хх в точке е равна:
- 1; - ее; - 2ее; - lnx. 17. Корень уравнения
- 2,5; - 0; - 1,5; - нет решения. 18. Наибольший корень уравнения
- - 2; - - такого корня нет. 19. Найдите модуль проекции вектора
- - 0; - - 8. 20. Сколько целых корней имеет уравнение - Ни одного - Один - Два - Три - Бесконечно много - Другой ответ 21. Сколько корней имеет уравнение - Ни одного - Один - Два - Бесконечно много - Другой ответ 22. Каково взаимное расположение плоскостей, заданных уравнениями x+y=1 и x–z=1? - Совпадают - Параллельны - Перпендикулярны - Пересекаются, но не перпендикулярны - Определить нельзя
23. Один из корней уравнения aх2 –7х + b =0 (a>0, b>0) равен a/4, другой равен b. Найти a+b. 4; 3; 5; 6; 2. 24. Длины параллельных сторон трапеции равны 25 см. и 4 см., а длины непараллельных сторон 20 см. и 13 см. Найдите высоту трапеции. 12; 13; 6; 7. 25. Если 50% числа равны
26. Если 70% числа равны
27. Количество целых значений параметра а, при которых абсцисса и ордината вершины параболы y=(х-11а)2-а2+10а-21положительны, равно… 6 4 2 5 3 28. Если в треугольнике две стороны равны 17см. и 25см., высота делит третью сторону на отрезки, разность которых равна 12см., то периметр треугольника равен… 40см. 50см. 60см. 70см. 30см. 29. Если сфера проходит через все вершины прямоугольного параллелепипеда с ребрами 2см, 5см, 6см, то площадь сферы равна… 63p 64p 65p 66p 60p 30. Количество корней уравнения 0 3 1 2 5 31. Сколько решений в натуральных числах имеет уравнение 3х + 4у = 42 Ни одного Одно Два Три Бесконечно много Другой отчет
32. Сколько целых корней имеет уравнение Ни одного Один Два Три Бесконечно много Другой ответ
33. Сколько корней имеет уравнение Ни одного Один Два Бесконечно много Другой ответ не имеют общей хорды. 34. Даны два различных положительных числа х и у. Что больше: Первое Второе Они равны Ответ зависит от конкретных значений х и у. 35. Разность сторон параллелограмма равна 2 см. Большая диагональ его равна 22 см, а меньшая диагональ равна большой стороне параллелограмма. Определите стороны параллелограмма. Стороны параллелограмма равны 11 см, 13 см 10 см, 12 см 13 см, 15 см 12 см, 14 см 36. Набор состоит из двух предметов. Цену одного из них увеличили на 60 %, а цену второго, который стоил в два раза дороже первого, увеличили на 30 %. В результате стоимость набора возросла на: 35% 90% 40% 45% 50% 37. К окладу прибавляется 25% районная надбавка, после чего взимается подоходный налог. Для того, чтобы получаемая на руки заработная плата равнялась окладу, подоходный налог должен составлять: 15% 25% 20% 22,5% 17,5% 38. Если сумма всех сторон прямоугольника равна 2, то его площадь не больше, чем: 1 2 3 1 4
39. Результат вычисления выражения
1, 0, -1,
- 40. Множество значений выражения [-2;0], [-1,125;0], [-1;1]; [0;1]; [0;1,125] 41. Многочлен 10х3 +3х2 -8х - 2 возвели в 100-ю степень. При этом получился многочлен с целыми коэффициентами. Обозначим через С1 модуль суммы всех его положительных коэффициентов, а через С2 модуль суммы всех его отрицательных коэффициентов. Оцените разность С1 – С2. Она равна нулю Она положительное однозначное число Она положительное число больше 9 Она отрицательное число больше – 100 Она отрицательное число меньше – 99 За отведённое время определить нельзя 42. Каково взаимное расположение плоскостей, заданных уравнениями x – y + z = 0 и y – x – z = 1? Совпадают Параллельны Перпендикулярны Пересекаются, но не перпендикулярны Определить нельзя 43. В какой координатной четверти находится точка перегиба графика функции у= ℮π + 3х5 + 5х4 + 10х3 + 30х2 +50х I II III IV Эта точка находится на одной из осей координат Число точек перегиба графика данной функции отлично от 1 44. Если сумма первых восьми членов геометрической прогрессии в 8 раз больше ее первого члена, а сумма первого, девятого, семнадцатого равна 9, то сумма первых двадцати четырех членов прогрессии равна 12; 24; 48; 60;
72 45. Вычислить: sin2α-3sinα·cosα-2cos2α, если
–2,6; –5,75; 1,9; ±3/Ö10; вычислить нельзя 46.
Решите уравнение 38/25; Ø; 9; -9; 25/13 47. Медианы треугольника делят его на шесть треугольников. Они … равновеликие неравновеликие равновеликие и неравновеликие попарно равновеликие и попарно неравновеликие 48. Найти наименьшее решение уравнения |x-2| x2-6x+8 =1; 1; 0; 2; нет решения. 49. Сумма корней уравнения |2*|х-1|-3|=5 равна: -8 -2 2 -3 50. Значение выражения arctg2+arctg3 равно: 1/5 π/4 -1 3/4π
|
||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.140.180 (0.011 с.) |

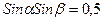 равна:
равна: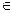 Z, если:
Z, если: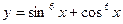 равна:
равна: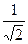
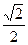
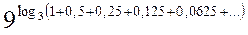 равно:
равно: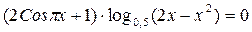 .
.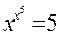 является
является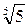
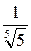
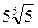
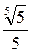
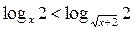 является
является 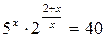 равен:
равен: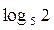 ;
;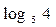 ;
;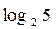 .
.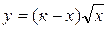 равно
равно 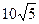 :
: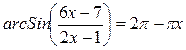 равен:
равен: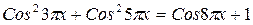 удовлетворяющий условию
удовлетворяющий условию 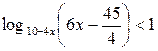 равно:
равно: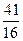 ;
;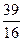 ;
;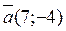 на ось, параллельную вектору
на ось, параллельную вектору 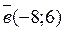 .
.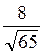 ;
;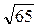 ;
;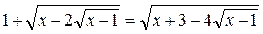 ?
?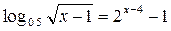 ?
?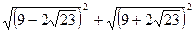 ,то это число равно…
,то это число равно…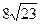
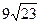
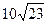

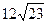
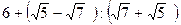 , то это число равно…
, то это число равно…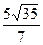
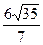
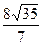
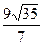
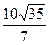
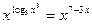 равно…
равно…
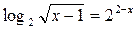 ?
? 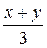 или
или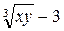 ?
?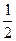
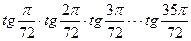 равен
равен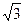 ,
,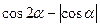 равно
равно