Б. Что русские (и нацисты) обнаружили в западных научных журналах:

Распад скалярных потенциалов на двухмерные продольные волны

Э.Т. Уиттекера

Итак, помня обо всем вышесказанном, зададимся важным вопросом: что именно русские отыскали в западных научных журналах? А также к какому заключению могли прийти немцы после изучения катушки Колера и что они так тщательно засекретили? Чтобы получить ответы на эти вопросы, необходимо вернуться к истории скалярного оружия.

Бирден утверждает, что в ходе научных поисков русским попались на глаза три статьи, маловразумительные, насыщенные математическими выкладками, абсолютно дорелятивистские и очень необычные. Две из них принадлежали авторству хорошо известного математика и физика-теоретика Е.Т. Уиттекера, и одна – физика по фамилии Барус. Статьи Уиттекера поражают воображение, и не в последнюю очередь потому, что их положения могут применяться в контексте разработанной позже квантовой теории.

Первая статья под названием «О неполных дифференциальных уравнениях математической физики» представляет собой настоящий шедевр, значение которого Уиттекер излагает в заключении (я выделил курсивом важные фрагменты, имеющие непосредственное отношение к анализу Бирдена, который приводится далее):

 

Из вышесказанного явствует, что поле силы, создаваемое притягивающимся телом, может быть разложено посредством «спектрального анализа» на бесконечное число составляющих полей; и хотя поле силы в целом не меняется со временем, каждое из составляющих полей носит волнообразный характер, состоя из простого волнового возмущения, распространяемого с однородной скоростью … В каждом из этих составляющих полей потенциал будет постоянным вдоль каждого фронта волны, и, следовательно, гравитационная сила в каждом составляющем поле будет перпендикулярна фронту волны, то есть волны будут продольными. [329]

 

Значение этого фрагмента можно легко упустить из вида, если забыть о том, что Уиттекер был еще и физиком, страстно верившим в эфир, то есть среду или механизм распространения электромагнитной энергии. Ведь именно он написал классическую историю концепции эфира. Обратите также внимание: эта статья была первоначально опубликована в Германии, и, следовательно, немцы едва ли могли не знать о ее существовании или о ее важности как явления нерелятивистской физики, тем более что они пытались объяснить странные аномалии катушки Колера и результаты своих экспериментов с радаром в конце войны. Действительно, их эксперименты с радаром и даже сам «Колокол» являются свидетельством того, что они упорно занимались скалярной физикой.

 

 

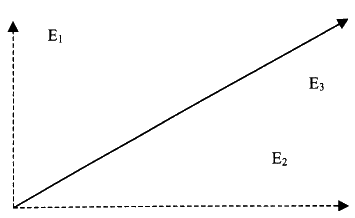
Для того чтобы понять, что Бирден подразумевает под скалярными волнами в среде или вакууме, мы должны узнать, с какого момента ортодоксальная физика пошла в неверном направлении. По мнению Бирдена, это произошло после Максвелла. Максвелл первым сформулировал свои уравнения на математическом языке, почти вымершем на сегодняшний день, который называется «геометрия кватернионов». Этот математический язык существенно отличается от стандартных линейной алгебры, тензорного исчисления и векторного анализа, на языке которых обычно излагается в учебниках и на лекциях стандартная электромагнитная теория. Другими словами, то, что сегодня изучают в учебниках и курсах физики как уравнения Максвелла, на самом деле не являются оригинальными уравнениями Максвелла! Это отредактированные уравнения. Но для того, чтобы уяснить, какой эффект оказывает на физику простая смена математического языка – с кватернионов на векторный анализ, – нам нужно понять несколько простых концепций.

Во-первых, существуют два типа воздействия, которое электромагнитные поля могут оказывать на заряженные частицы: (1) смещение и (2) напряжение. Существуют два типа смещения, или движения. Первый тип – простое смещение по прямой линии, порождающее электрическое поле, или поле «Е». Второй тип – движение по спирали, порождающее поле, математически обозначаемое как поле «В». Пока мы не будем касаться последнего.

Теперь предположим, что имеются два вектора, Е₁и Е₂, воздействующие на частицу, как показано на диаграмме:

В результате происходит смещение в направлении вектора Е₃, так как два вектора складываются и дают в сумме то, что называется «результирующим» вектором. Таким образом, в системах, где действует много векторов смещения, «вся система может быть заменена одним-единственным вектором», результирующим вектором, который описывает реальное смещение, происходящее под воздействием первоначальных векторов. [330]

 

 

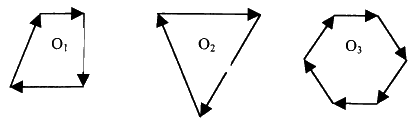
Теперь заметьте, что если смещения не происходит, результирующий вектор является нулевым вектором. Однако всегда следует помнить, что мы имеем дело с геометрией, а не просто с математикой или числами. Следовательно, можно предусмотреть множество мультивекторных систем, имеющих нулевой вектор смещения, которые, тем не менее, обладают самыми различными внутренними напряжениями и геометрией:

Если мыслить исключительно категориями условностей линейной алгебры и, соответственно, заменять мультивекторные системы результирующим вектором, то каждая из трех систем, изображенных на приведенной выше диаграмме, будет заменена нулевым результирующим вектором. Это означает, что внутренние напряжения систем и их вращательные характеристики – все явно очень разные – заменяются нулевым вектором, и, таким образом, три разные системы ошибочно считаются физически эквивалентными в силу математической условности!

Теперь мы в состоянии понять, что такое скаляр и почему Максвелл намеренно выбрал геометрию кватернионов для записи своих уравнений: ибо он думал при этом именно о типах ситуаций физического напряжения, которые изображаются вихрями на приведенной выше диаграмме.

В стандартной линейной алгебре каждая стрелка системы математически была бы представлена следующим образом:

 

v = ai + bj +ck

 

Таким образом, если общая сумма всех таких векторов не дает смещения, все подобные математические выражения заменяются нулевым вектором. Но, как мы уже видели, каждая система содержит внутреннее вращение или напряжение, стало быть, что-то остается. Возникает вопрос: как выразить это математически?

Кватернион – это скаляр плюс вектор, а скаляр – это чистая величина, число, которое не имеет направления. Он просто есть. Таким образом, кватернион (q) – это скаляр (s) плюс вектор (v):

 

q = s + v

 

Вставив в эту формулу наше предыдущее выражение для вектора, получаем:

 

q = s + ai + bj + ck

 

Таким образом, для представленной выше системы шестиугольной формы мы имеем шесть различных выражений типа q = s + ai + bj + ck. Теперь представим, что мы умножаем каждый из этих векторов. Согласно правилам умножения линейной алгебры, нуль, умноженный на нуль, равняется нулю. Итак, в линейной алгебре дело опять кончается ничем, нулевым вектором, поскольку никакого смещения не было. Но в геометрии кватернионов скаляры, которые не равны нулю, при умножении дают следующий результат:

 

q х q = s 2+ t 2+ и 2+ w 2+ x 2+ у 2+ 0 V,

 

где 0 V– нулевой вектор, а величины в квадрате – умноженные скаляры. Следовательно, в геометрии кватернионов внутреннее напряжение сохраняется даже при отсутствии смещения. Скаляры, таким образом, представляют чистые величины силы, запертой внутри структуры, не имеющей ни направления, ни смещения.

Теперь мы в состоянии понять, что представляет собой скалярная физика: это не стандартная векторная или линейная физика в каком бы то ни было смысле, это нелинейная   физика внутренних напряжений в локальной среде.

Мы также в состоянии понять смысл заключения статьи Уиттекера, приведенного выше, смысл, вполне очевидный благодаря анализу Бирдена:

 

Интерференция скалярных потенциалов – каждый из которых представляет собой комплект продольных (электромагнитных) волн и вовсе не скалярную, а мультивекторную сущность – создает (электромагнитные) поля, а также волны и их динамику. На основании этого мы делаем предположение, что интерференция распространяющихся переупорядоченных сущностей (электромагнитной) энергии, имеющая место в любой точке пространства, порождает энергетические колебания (электромагнитного) поля нулевой точки самого вакуума. В самом деле, статья Эванса… уже продемонстрировала, что именно такая скалярная интерферометрия создает поперечные (электромагнитные) поля и волны в вакууме на расстоянии. [331]

 

Другими словами, нужно представлять каждую из скалярных сущностей, сопровождающих векторы на приведенных выше диаграммах, состоящими из двухмерных продольных или акустических волн в среде. Таким образом, Уиттекер разлагает скалярные сущности на пары таких волн давления или напряжения в среде. Объединение или интерференция таких волн создает стандартные электромагнитные поля и волны, наблюдаемые в ортодоксальной физике. И, что самое важное, это можно делать на расстоянии.

Но что это означает?

Говоря простым языком, поскольку каждый атом каждого типа состоит из частиц с зарядом и/или массой, он имеет свой особый скалярный показатель или резонанс (вспомните приведенные выше диаграммы и представьте математические обозначения, которые описывали бы каждый из них в геометрии кватернионов). Таким образом, чтобы оказать воздействие на любую из этих систем, нужно просто, так сказать, двигаться назад и конфигурировать ее скалярный показатель, разлагая каждый из скаляров на пару двухмерных продольных импульсов и волн.

Итак, существуют бесчисленные типы систем нулевых суммарных векторов, а приведенная выше диаграмма – это шаблон действия, или, по выражению Бирдена, «робот причинной системы», шаблон достижения нужного результата в системе на расстоянии посредством конфигурирования резонанса в соответствии с его скалярным показателем:

 

При наличии достаточной теоретической подготовки можно двигаться назад, чтобы получить нужную причинную систему… соответствующую той или иной физической системе… Тем самым создается детерминистический комплект искривлений пространства-времени и запечатленная динамика, которые мы называем двигателем… Встраивая скалярные интерферометрические функции, «роботу причинной системы» можно придать оружейные возможности, и т. д. [332]

 

То есть вы воспроизводите скалярный топологический показатель системы, на которую вам нужно оказать влияние (или которую вам нужно разрушить), и загружаете в нее соответствующую информацию:

 

Если собирать нужные двухволновые субкомплекты (продольных) волн, два скалярных потенциала и их результирующая несущая волна, возникшая в результате интерференции, структурируются внутренне как нужно. Это использование так называемого внутреннего информационного содержания поля. Мы говорим о намеренно структурированных потенциале, поле или волне как об обусловленных, получивших размерности или активированных. Если эти термины кажутся вам не очень подходящими, используйте более общий термин «внутренне структурированные». [333]

 

В соответствии с хорошо известным механизмом преобразования «масса-энергия» масса и инерция являются «прямым результатом поглощенного скалярного резонанса, а также им самим». Но что такое «поглощенный скалярный резонанс»? Механизмом поглощения является спин частицы, [334] то есть внутренние вращательные напряжения или вихри в среде различных систем – подобных тем, что изображены на приведенной выше диаграмме. [335]

В большей степени, нежели что-либо другое, способность конфигурировать шаблон на основе скалярного показателя и его резонансных эффектов на больших расстояниях позволяет производить действие на дистанции, величина которой дала основание британскому разведчику говорить о «в высшей степени необычных областях физики» в беседе с немецкими исследователями Майером и Менером. Это действительно очень сложная форма магии.

Результатом исследований в этой новой области физики стало положение, согласно которому пространство само по себе обладает структурой и содержанием; среда или эфир могут рассматриваться как большой комплект скалярных потенциалов, которые могут быть разложены на пары продольных волн. И поскольку скаляр представляет собой внутреннее вращательное напряжение, скалярная физика является не только нелинейной, но и вихревой.