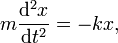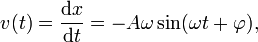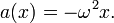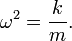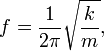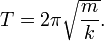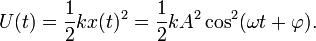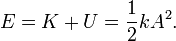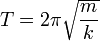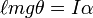Динамика простого гармонического движения

Для колебания в одномерном пространстве, учитывая Второй закон Ньютона (F = m  d² x /d t ²) и закон Гука (F = − kx, как описано выше), имеем линейное дифференциальное уравнение второго порядка:

где

m — это масса тела,

x — его перемещение относительно положения равновесия,

k — постоянная (коэффициент жёсткости пружины).

Решение этого дифференциального уравнения является синусоидальным; одно из решений таково:

где A, ω, и φ — это постоянные величины, и положение равновесия принимается за начальное.^[1] Каждая из этих постоянных представляет собой важное физическое свойство движения: A — это амплитуда, ω = 2π f — это круговая частота, и φ — начальная фаза.^[2]

Положение, скорость и ускорение гармонического осцилятора

Используя приёмы дифференциального исчисления, скорость и ускорение как функция времени могут быть найдены по формулам:

 

Положение, скорость и ускорение простого гармонического движения на фазовой плоскости

Ускорение может быть также выражено как функция перемещения:

Поскольку ma = − mω ² x = − kx, то

Учитывая, что ω = 2π f, получим

и поскольку T = 1/ f, где T — период колебаний, то

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Энергия простого гармонического движения

Кинетическая энергия K системы в функции времени t такова:

и потенциальная энергия есть

Полная механическая энергия системы, однако, имеет постоянное значение

Примеры

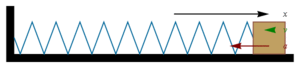
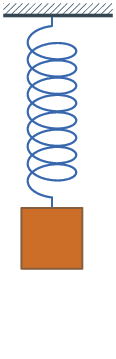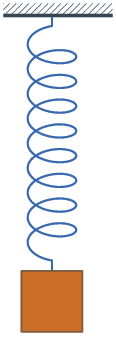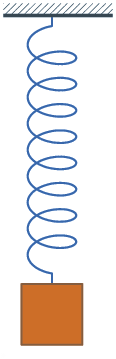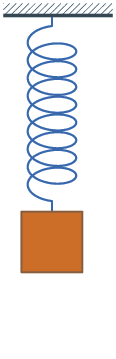
Система груз-пружина без затухания, в которой происходит простое гармоническое движение.

Простое гармоническое движение представлено в различных простых физических системах, и ниже приведены некоторые примеры.

Груз на пружине

Масса m, прикреплённая к пружине с постоянной жёсткостью k является примером простого гармонического движения в пространстве. Формула

показывает, что период колебаний не зависит от амплитуды и ускорения свободного падения.

Универсальное движение по окружности

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерная проекция универсального движения по окружности. Если объект движется с угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x - y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

Движение маятника, не имеющего затуханий, можно приближённо рассматривать как простое гармоническое движение, если амплитуда колебаний очень мала в сравнении с длиной стержня.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ с ускорением свободного падения g даётся формулой

Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от ускорения свободного падения g, поэтому при той же самой длине маятника, на Луне он будет вращаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах, поскольку выражение для углового ускорения пропорционально синусу координаты:

где

I — момент инерции; в данном случае I = m ℓ ².

Когда угол θ мал, можно считать, что sin  θ ≈ θ, и выражение принимает вид:

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.