
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные гармонические колебания. Гармонический осциллятор.Содержание книги
Поиск на нашем сайте
Периодические колебания называются гармоническими, если они описываются законами sin или cos. Любая колеблющаяся система, любой физический процесс, описываемый законами sin или cos называется гармоническим осциллятором или просто осциллятором. Примеры: Дифференциальное уравнение свободных гармонических колебаний
Первоначально система находится в равновесии
Систему вывели из положения равновесия на
груза на пружине. Решение его есть
что проверяется непосредственной подстановкой. Физический маятник – это любое твердое тело, колеблющееся относительно оси, не проходящей через его центр. Если ось проходит через центр тяжести, то тело находится в состоянии безразличного равновесия и колебаться не будет. Ось вращения проходит через точку О. Центр тяжести
По второму закону Ньютона
Знак (-) означает, что тело стремится в равновесие. Теперь
Это нелинейное дифференциальное уравнение, в него входит
Уравнение
- это однородное линейное дифференциальное уравнение второго порядка. Оно описывает гармонические колебания. Это частный случай физического маятника. Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. (Груз, подвешенный на нерастяжимой длинной нити, размерами груза по сравнению с длиной нити можно пренебречь): При многих расчетах удобно представить формулу периода физического маятника как математического. Вводят приведенную длину физического маятника
Тогда
Приведенной длиной физического маятника называется длина такого маятника, период колебания которого равен периоду колебания данного физического маятника. Экспериментально, введя
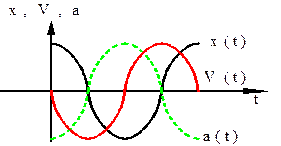
Продолжим рассмотрение гармонических колебаний.
1) 2) 3) 4) Связь Рассмотрим значение осциллирующего параметра в моменты
Скорость опережает смещение по фазе на
Сдвиг фаз между «МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ» План лекции
1. Колебательное движение. Гармоническое колебание. 2. Скорость и ускорение гармонического колебания. 3. Энергия гармонического колебательного движения. 4. Свободные колебания. Гармонический осциллятор. 5. Пружинный, математический и физический маятники. 6. Вынужденные колебания. Резонанс. Автоколебания. 7. Примеры проявления резонансных явлений в живых организмах. 8. Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение
1. Колебательное движение. Гармоническое колебание.
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.135 (0.009 с.) |


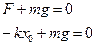
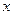 . Деформация будет
. Деформация будет  .
.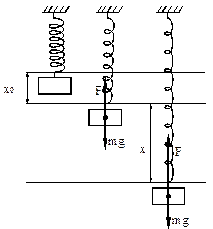
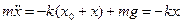 Преобразуем выражение к виду
Преобразуем выражение к виду 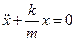 . Обозначим
. Обозначим 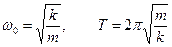 . Получим
. Получим 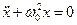 . Это линейное однородное дифференциальное уравнение второго порядка. Оно описывает колебания
. Это линейное однородное дифференциальное уравнение второго порядка. Оно описывает колебания
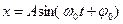 ,
,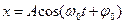 ,
,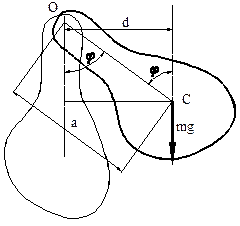
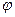 - угол поворота. В точке С приложена сила тяжести, в точке О – сила реакции, она направлена вертикально вверх. Поскольку она проходит через ось вращения, то ее момент равен нулю. Вращающий момент создает сила
- угол поворота. В точке С приложена сила тяжести, в точке О – сила реакции, она направлена вертикально вверх. Поскольку она проходит через ось вращения, то ее момент равен нулю. Вращающий момент создает сила 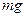 .
. 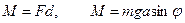 . Этот вращающий момент стремится вернуть тело к положению равновесия.
. Этот вращающий момент стремится вернуть тело к положению равновесия.
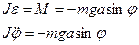
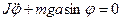 .
.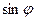 . Поэтому в общем случае физический маятник колеблется не по гармоническому закону. Рассмотрим частный случай, когда
. Поэтому в общем случае физический маятник колеблется не по гармоническому закону. Рассмотрим частный случай, когда 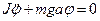 ,
, 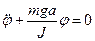 ,
, 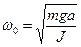 ,
, 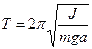 .
.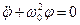
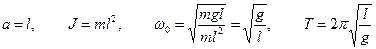 - формула Гюйгенса.
- формула Гюйгенса.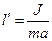 .
.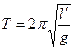 .
.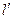 , определяют
, определяют 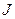 любого маятника. Подбирают длину математического маятника, чтобы
любого маятника. Подбирают длину математического маятника, чтобы 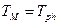 . Тогда
. Тогда 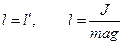 . Определяя
. Определяя 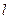 и
и 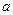 , находят
, находят 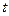 ).
).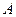 - амплитуда – максимальное отклонение от положения равновесия, или максимальное значение осциллирующего параметра,
- амплитуда – максимальное отклонение от положения равновесия, или максимальное значение осциллирующего параметра, 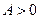 всегда.
всегда.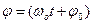 - фаза колебания, измеряется в радианах, фаза определяет значение осциллирующего параметра в любой момент времени.
- фаза колебания, измеряется в радианах, фаза определяет значение осциллирующего параметра в любой момент времени. 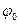 - начальная фаза в нулевой момент времени.
- начальная фаза в нулевой момент времени.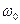 - собственная циклическая (круговая) частота.
- собственная циклическая (круговая) частота.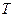 .
.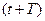 , где
, где 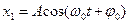 ,
,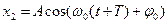 ,
,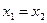
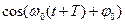 =
= 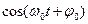 .
.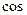 могут отличаться на
могут отличаться на 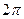 .
.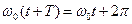 ,
, 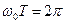 ,
,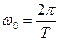 ,
, 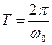 ,
, 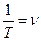 ,
, 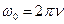 ,
,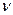 - число колебаний за 1 с,
- число колебаний за 1 с, 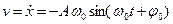 =
= 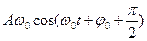
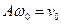 - амплитудное значение скорости
- амплитудное значение скорости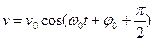
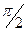 .
.
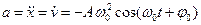 =
= 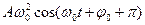

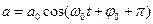
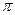 , они колеблются в противофазах.
, они колеблются в противофазах.


