
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Система параллельных сил.Содержание книги
Поиск на нашем сайте
а) Параллельные силы направлены в одну сторону.
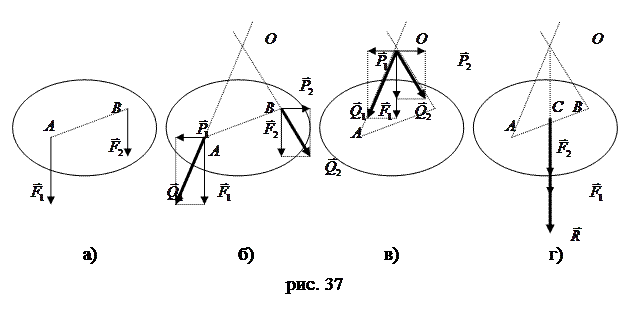
Рассмотрим твердое тело, на которое действуют две параллельные силы 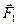 и и 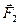 , приложенные в точках , приложенные в точках 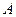 и и 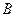 тела (рис.37а). Требуется определить модуль и точку приложения равнодействующей этих двух сил. тела (рис.37а). Требуется определить модуль и точку приложения равнодействующей этих двух сил.
Пользуясь аксиомами 1 и 2 статики, перейдем от данной системы параллельных сил к эквивалентной системе сходящихся сил
33 Полученные в результате такого сложения силы В результате в точке или учитывая, что Таким образом, равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в ту же сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных силам.
б) Антипараллельные силы. Докажем теорему: равнодействующая двух антипараллельных сил параллельна этим силам и направлена в сторону большей из них. Модуль равнодействующей равен разности модулей данных сил, а линия действия равнодействующей делит расстояния между точками приложения данных сил внешним образом на части, обратнопропорциональные этим силам.
Рассмотрим твердое тело, на которое действуют две антипараллельные силы 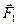 и и 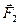 , приложенные в точках , приложенные в точках 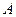 и и 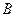 тела и при этом тела и при этом 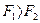 (рис.38а). Требуется определить модуль и точку приложения равнодействующей этих двух сил. Заменим силу (рис.38а). Требуется определить модуль и точку приложения равнодействующей этих двух сил. Заменим силу 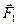 двумя эквивалентными силами двумя эквивалентными силами 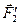 , приложенной в точке , приложенной в точке 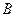 , причем , причем 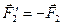 и силой и силой 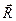 , приложенной в точке , приложенной в точке 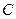 . . 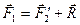 , , 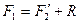 и учитывая, что и учитывая, что 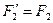 , , 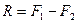 , , 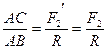 отсюда отсюда34
Преобразуем равенство Центр параллельных сил. Центр тяжести. Сложим две параллельные силы
Рассматривая векторные треугольники, составляем соотношения между векторами: Если по аналогичной процедуре, рассмотреть сложение трех и более параллельных сил, то, обобщая эти результаты, получаем зависимость, определяющую точку приложения равнодействующей: Если спроектировать векторное равенство (11) на оси декартовой системы координат, то получим выражения, определяющие координаты точки 35 Следует отметить, что если параллельные силы повернуть вокруг их точек приложения на один и тот же угол, то равнодействующая повернется на тот же угол, но координаты точки Т.о. центром параллельных сил называется такая точка, через которую проходит равнодействующая системы при любом ее направлении. В качестве примера, можно рассмотреть тело, находящееся в поле тяжести земли. Каждая частица этого тела испытывает силу притяжения со стороны земли. С учетом того, что расстояния между этими частицами по сравнению с радиусом земли малы, можно считать такую систему сил параллельной. Равнодействующая такой системы называется весом тела, а точка приложения центром тяжести, координаты которой определяются по зависимостям (12).
Тема 9. Кинематика. Кинематика точки. Основные понятия. Кинематико й называется раздел механики, в котором изучаются геометрические свойства движение материальных тел без учета их инертности (массы), а также причин, вызывающих данное движение (сил). Кинематика представляет собой, с одной стороны, введение в динамику, так как здесь вводятся основные понятия и зависимости необходимые для изучения движения тел с учетом действия сил. С другой стороны, методы кинематики имеют и самостоятельное практическое значение, например, при изучении передач движения в механизмах. Под движением в механике понимается изменение с течением времени положения данного тела в пространстве по отношению к другим телам. Для определения положения движущегося тела с тем телом, по отношению к которому изучается движение, жестко связывают какую – нибудь систему осей координат, которую будем называть системой отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к данной системе отсчета находится в покое (этот случай рассматривался в разделе статика). Если же координаты, каких – нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе отсчета находится в движении. Движение тел совершается в пространстве с течением времени. Пространство в механике рассматривается, как трехмерное, а время считается универсальным, т.е. протекающим одинаково во всех системах отсчета. Время является скалярной, непрерывно меняющейся величиной. В задачах кинематики оно принимается за независимую переменную (аргумент), а все остальные величины (координаты, скорости и т.д.) рассматриваются как функции этого аргумента. Кинематику делят на кинематику точки и кинематику системы материальных точек (тела). В кинематике решаются две основные задачи: - первая задача состоит в установлении математических способов задания движения точек или тел; 36 - вторая задача заключается в том, чтобы, зная закон движения данного тела или точки, определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности. Для решения задач кинематики необходимо, чтобы непосредственно был задан или закон движения данного тела или же закон движения, какого – нибудь другого тела, кинематически связанного с данным.
Способы задания движения точки. Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех способов: естественный, координатный, векторный. 1. Естественный способ задания движения точки. Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным. Пусть точка
Тогда положение точки При движении точка Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным способом, необходимо знать: 37 1. Траекторию движения точки; 2. Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3. Закон движения точки вдоль траектории Следует отметить, что величина
2.Координатный способ задания движения точки. В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы осей (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде: При координатном способе задания движения точки, траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории. При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).
38 Положение точки в этом случае будут определять полярный угол 3.Векторный способ задания движения точки. В этом случае положение точки в пространстве определяется только радиусом – вектором, проведенным из начала декартовой системы координат (рис. 43). Уравнение движения в этом случае имеет вид: Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трех скалярных.
Связь между различными способами задания движения. В этом параграфе показано, как можно сделать переход от одного способа задания движения точки к другому. а) Переход от координатного способа задания движения к векторному. Эту связь легко получить, если ввести единичные векторы (орты) осей По зависимости (16), можно сделать переход от координатного способа задания движения к векторному, и наоборот б) Переход от координатного способа задания движения к естественному. Допустим, что движение задано в виде уравнений (14). Известно, что
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.19.124 (0.01 с.) |

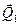 и
и 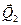 . Для этого приложим в точках
. Для этого приложим в точках 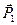 и
и 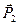 , направленные вдоль прямой
, направленные вдоль прямой 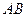 и сложим силы
и сложим силы 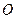 и раскладываем обратно на составляющие
и раскладываем обратно на составляющие 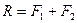 (рис. 37г). Для определения точки приложения силы
(рис. 37г). Для определения точки приложения силы 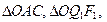
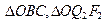 (рис. 37в).
(рис. 37в). 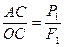 ,
, 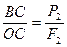
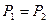 ,
, 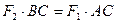 .
. 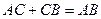 , получаем
, получаем 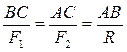 . (10)
. (10)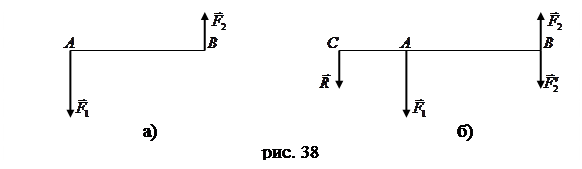
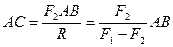 . Это равенство определяет положение точки
. Это равенство определяет положение точки 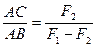 ,
, 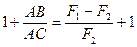 ,
, 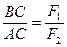 ,
, 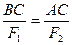 . Из последней полученной зависимости видно, что в этом случае линия действия равнодействующей
. Из последней полученной зависимости видно, что в этом случае линия действия равнодействующей 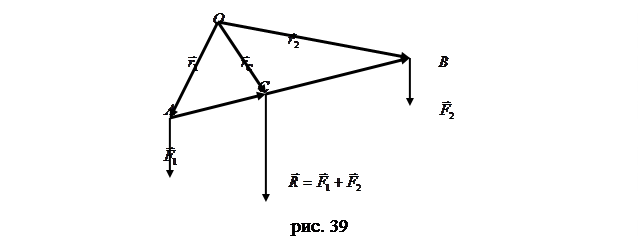
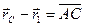 ,
, 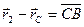 . Кроме того, по зависимости (10):
. Кроме того, по зависимости (10): 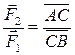 ,
, 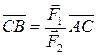 ,
, 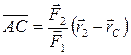 ,
, 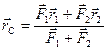 .
.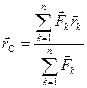 (11)
(11)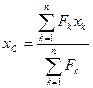 ,
, 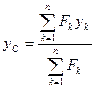 ,
, 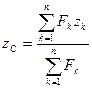 (12)
(12) движется относительно системы отсчета, вдоль некоторой траектории
движется относительно системы отсчета, вдоль некоторой траектории 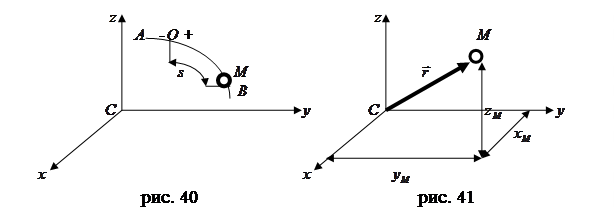
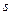 , равной расстоянию от точки
, равной расстоянию от точки 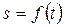 (13)
(13)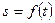 .
. 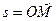 , а пройденный за это время движения путь будет равен
, а пройденный за это время движения путь будет равен 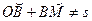 .
.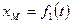 ,
, 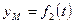 ,
, 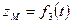 (14)
(14)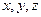 , которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.
, которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.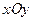 , получаем два уравнения движения
, получаем два уравнения движения 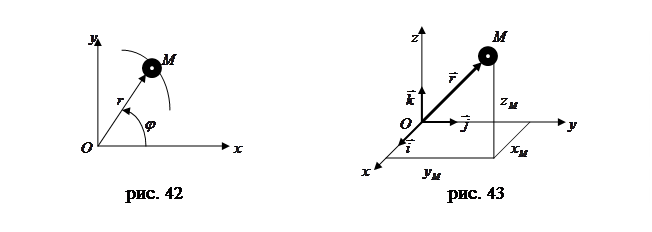
 и вектор
и вектор  , т.е. уравнения движения точки в полярных координатах имеют вид:
, т.е. уравнения движения точки в полярных координатах имеют вид: 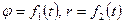 .
.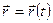 (15)
(15)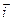 ,
, 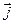 ,
, 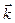 (рис. 43). Тогда учитывая, что проекции вектора
(рис. 43). Тогда учитывая, что проекции вектора 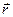 на оси
на оси 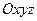 равны координатам точки
равны координатам точки 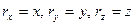 , получаем:
, получаем: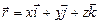 (16)
(16)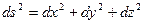 или
или 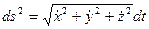 , где
, где 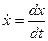 ,
, 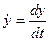 ,
, 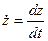 . Отсюда получаем:
. Отсюда получаем: 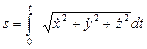 (17)
(17)


