
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорений точек плоской фигуры.⇐ ПредыдущаяСтр 15 из 15
При определении ускорений точек плоской фигуры, прослеживается аналогия с методами определения скоростей. 1. Метод полюса. Также как и при определении скоростей, принимаем за полюс произвольную точку тела, ускорение которой нам известно, или мы можем его определить. Тогда, ускорение любой точки плоской фигуры равно сумме ускорений полюса и ускорения во вращательном движении вокруг этого полюса. При этом составляющая
Тогда зависимость (58) принимает вид: Учитывая зависимости (51) и (52), получаем
2. Мгновенный центр ускорений. Мгновенным центром ускорений (МЦУ) называется точка твердого тела, ускорение которой в данный момент времени равно нулю. 59 Покажем, что в каждый данный момент времени такая точка существует. Принимаем за полюс точку Действительно, ускорение точки
Следовательно,
Частные случаи определения МЦУ. 1. 2. 3. 4.
Из рассмотренных частных случаев можно сделать вывод: если принять точку
60
Сложным движением материальной точки называется такое движение, при котором точка одновременно участвует в двух или боле движениях. При таком движении положение точки определяют относительно подвижной и относительно неподвижной систем отсчета. Движение точки относительно подвижной системы отсчета называется относительным движением точки. Параметры относительного движения условимся обозначать Движение той точки подвижной системы отсчета, с которой в данный момент совпадает движущаяся точка, относительно неподвижной системы отсчета называется переносным движением точки. Параметры переносного движения условимся обозначать Движение точки относительно неподвижной системы отсчета называется абсолютным (сложным)движением точки. Параметры абсолютного движения условимся обозначать В качестве примера сложного движения, можно рассмотреть движение человека в движущемся транспорте (трамвай). В этом случае движение человека отнесено к подвижной системе координат – трамваю, и к неподвижной системе координат – земля (дорога). Тогда исходя из данных выше определений, движение человека относительно трамвая – относительно, движение вместе с трамваем относительно земли – переносное, а движение человека относительно земли – абсолютное.
Будем определять положение точки
61
Получим условия (ограничения), соответствующие относительному, переносному и абсолютному движениям. 1. При рассмотрении относительного движения, будем считать, что точка
2. При рассмотрении переносного движения, будем считать, что координаты точки
3. При абсолютном движении точка движется и относительно
Тогда выражения для скоростей, с учетом (27), имеют вид:
62 Сравнивая эти зависимости, получаем выражение для абсолютной скорости: Получили теорему о сложении скоростей точки в сложном движении: абсолютная скорость точки равна геометрической сумме относительной и переносной составляющих скорости.
Используя зависимость (31), получаем выражения для ускорений:
Получили, что абсолютное ускорение точки не равно геометрической сумме относительной и переносной составляющих скоростей. Определим составляющую абсолютного ускорения, стоящую в скобках, для частных случаев.
1. Переносное движение точки поступательное
Если переносное движение точки поступательное, то абсолютное ускорение точки равно геометрической сумме относительной и переносной составляющей ускорения.
2. Переносное движение точки непоступательное. Значит, в этом случае подвижная система координат 63 С другой стороны,
В общем случае абсолютное ускорение точки равно геометрической сумме относительной и переносной составляющей ускорения плюс удвоенное векторное произведение вектора угловой скорости переносного движения на вектор линейной скорости относительного движения.
Удвоенное векторное произведение вектора угловой скорости переносного движения на вектор линейной скорости относительного движения называется ускорением Кориолиса и обозначается: Ускорение Кориолиса характеризует изменение относительной скорости в переносном движении и изменение переносной скорости в относительном движении. Направляется Модуль ускорения Кориолиса равен:
64
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.039 с.) |
 (58)
(58) определяет ускорение точки
определяет ускорение точки 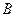 при ее вращении вокруг полюса
при ее вращении вокруг полюса 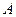 . При вращении траектория движения точки будет криволинейной, а значит
. При вращении траектория движения точки будет криволинейной, а значит 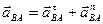 (рис. 66).
(рис. 66).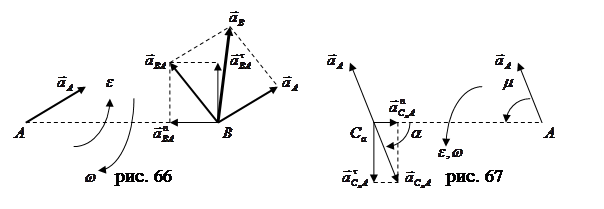
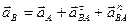 (59)
(59) ,
, 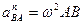 .
. нам известно. Находим угол
нам известно. Находим угол 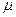 , лежащий в пределах
, лежащий в пределах 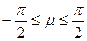 , и удовлетворяющий условию
, и удовлетворяющий условию  . Если
. Если 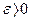 , то
, то  и наоборот, т.е. угол
и наоборот, т.е. угол 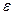 . Отложим от точки
. Отложим от точки 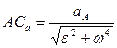 (рис. 67). Полученная такими построениями точка
(рис. 67). Полученная такими построениями точка 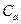 будет МЦУ.
будет МЦУ. во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 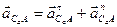 .
.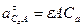 ,
,  . Тогда
. Тогда  . С другой стороны, ускорение
. С другой стороны, ускорение  угол
угол  , который удовлетворяет условию:
, который удовлетворяет условию:  . Знак минус, т.к. вращение
. Знак минус, т.к. вращение 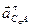 относительно полюса
относительно полюса 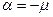 .
.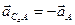 и тогда
и тогда 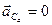 .
.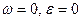 . Тогда
. Тогда  , и, следовательно, МЦУ не существует. В этом случае тело движется поступательно, т.е. скорости и ускорения всех точек тела равны.
, и, следовательно, МЦУ не существует. В этом случае тело движется поступательно, т.е. скорости и ускорения всех точек тела равны.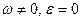 . Тогда
. Тогда 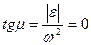 ,
,  . Значит, МЦУ лежит на пересечении линий действия ускорений точек тела (рис.68а).
. Значит, МЦУ лежит на пересечении линий действия ускорений точек тела (рис.68а).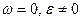 . Тогда
. Тогда 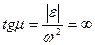 ,
, 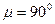 . Значит, МЦУ лежит на пересечении перпендикуляров к ускорениям точек тела (рис.68б).
. Значит, МЦУ лежит на пересечении перпендикуляров к ускорениям точек тела (рис.68б).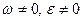 . Тогда
. Тогда 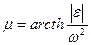 . Значит, МЦУ лежит на пересечении лучей, проведенных к ускорениям точек тела под углом
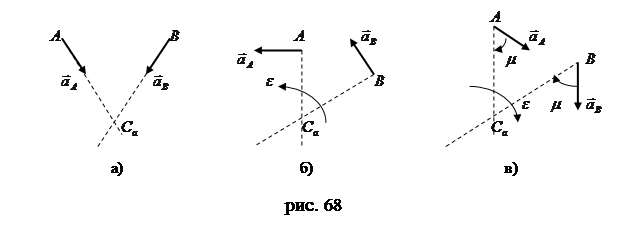
. Значит, МЦУ лежит на пересечении лучей, проведенных к ускорениям точек тела под углом 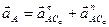 (60)
(60)
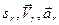 .
.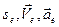 .
.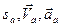 .
.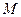 радиусами – векторами относительно подвижной
радиусами – векторами относительно подвижной 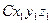 и неподвижной
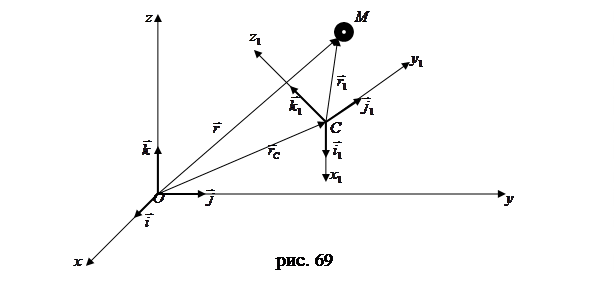
и неподвижной 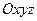 систем координат (рис. 69). Введем обозначения:
систем координат (рис. 69). Введем обозначения: - радиус-вектор, определяющий положение точки
- радиус-вектор, определяющий положение точки 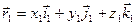 ;
;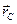 - радиус-вектор, определяющий положение начала подвижной системы координат (точки
- радиус-вектор, определяющий положение начала подвижной системы координат (точки 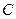 ), относительно неподвижной системы координат (точки
), относительно неподвижной системы координат (точки 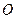 );
);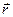 - радиус – вектор, определяющий положение точки
- радиус – вектор, определяющий положение точки  ,
,  ;
;
 .
.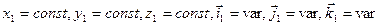 .
.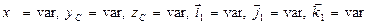 .
. ,
, 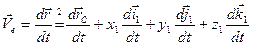 ,
,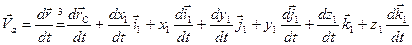 .
.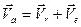 (61)
(61)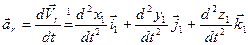

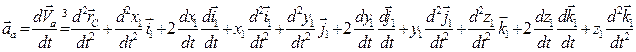 Сравнивая эти зависимости, получаем выражение для абсолютного ускорения:
Сравнивая эти зависимости, получаем выражение для абсолютного ускорения: .
.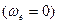 . В этом случае оси подвижной системы координат
. В этом случае оси подвижной системы координат 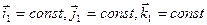 .
.  ,
, 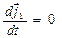 ,
, 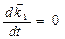 , тогда
, тогда 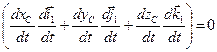 . Окончательно получаем:
. Окончательно получаем: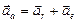 (62)
(62)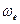 (рис. 70). Обозначим точку на конце вектора
(рис. 70). Обозначим точку на конце вектора 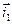 через
через 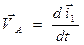 .
.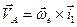 . Приравнивая правые части этих векторных равенств, получаем:
. Приравнивая правые части этих векторных равенств, получаем: 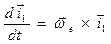 . Поступая аналогично, для остальных орт векторов, получаем:
. Поступая аналогично, для остальных орт векторов, получаем:  ,
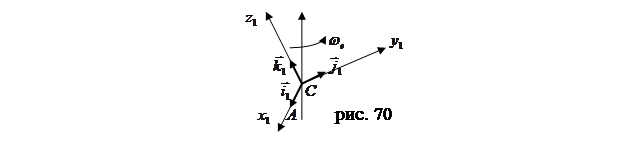
, 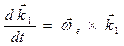 .
.
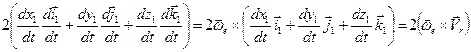
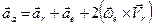 (63)
(63) (64)
(64)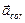 по правилу векторного произведения. Вектор ускорения Кориолиса всегда направлен перпендикулярно плоскости, которую образуют вектора
по правилу векторного произведения. Вектор ускорения Кориолиса всегда направлен перпендикулярно плоскости, которую образуют вектора  и
и 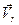 , таким образом, чтобы, смотря с конца вектора
, таким образом, чтобы, смотря с конца вектора 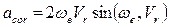 (65)
(65)


