
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Система сходящихся сил. Условия равновесия системы сходящихся сил.Стр 1 из 15Следующая ⇒
Типы опор (связей) 1. Гладкая поверхность. Гладкой будем называть поверхность, трением о которую данного тела в первом приближении можно пренебречь. Эта связь не дает телу перемещаться только по направлению общей нормали к поверхностям соприкасающихся тел в точке их касания (рис. 1). Поэтому реакция
рис. 1 рис.2 2. Гибкая нерастяжимая нить.
рис. 3 рис.4 9 3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром. Осевая линия болта называется осью шарнира. Тело
4. Шаровой (сферический) шарнир и подпятник.
Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. Примерами таких связей служат шаровая пята, с помощью которой прикрепляется фотоаппарат к штативу и подшипник с упором (подпятник) (рис. 5). Реакция 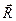 шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее заранее не известны ни модуль реакции шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее заранее не известны ни модуль реакции 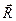 , ни углы, образуемые ею с осями , ни углы, образуемые ею с осями 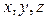 . .
5. Стержень. Пусть в какой-нибудь конструкции связью является стержень 10 6. Жесткая заделка. В этом случае конец балки защемлен между опорными плоскостями. Этот тип опорного закрепления препятствует любому отрыву от себя, а также вращению. Таким образом, данный тип опоры дают неизвестные составляющие реакции
Принцип освобождения от связей. Любое несвободное тело можно рассматривать как свободное, если связи, наложенные на тело отбросить и заменить их действие реакциями этих связей. Этот принцип позволяет свести изучение равновесия несвободного тела к изучению равновесия свободного тела. Например, брус
рис. 8а рис.8б
Эквивалентность пар. Теорема. Две пары, лежащие в одной плоскости и имеющие численно равные моменты и одинаковые направления вращения, эквивалентны. Доказательство: даны две пары
Продлеваем линии действия этих сил и получаем линию пересечения АВ плоскостей пар  и и 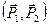 (рис. 22б). Далее, переносим силы (рис. 22б). Далее, переносим силы 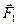 и и 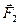 вдоль линий их действия в точки А и В соответственно и раскладываем силы на составляющие вдоль линий их действия в точки А и В соответственно и раскладываем силы на составляющие 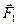 на на 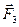 и и 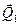 , а , а 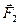 на на 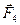 и и 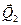 (рис. 22в). Причем (рис. 22в). Причем 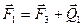 , , 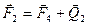 , и линии действия сил , и линии действия сил 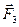 и и 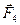 направлены вдоль АС и ВЕ соответственно, а силы направлены вдоль АС и ВЕ соответственно, а силы 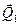 и и 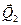 прямопротивоположные и направлены вдоль АВ. На основании аксиомы 2, не изменяя состояния тела, силы прямопротивоположные и направлены вдоль АВ. На основании аксиомы 2, не изменяя состояния тела, силы 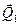 и и 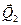 можно отбросить, и в результате мы получаем пару сил с плечом можно отбросить, и в результате мы получаем пару сил с плечом 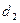 (рис. 22г). (рис. 22г).
19 Покажем, что момент полученной пары Из доказанной теоремы получаем следующие следствия. Следствие 1. Данную пару, не изменяя ее действия на тело, можно как угодно переносить в ее плоскости действия. Следовательно, действие пары на тело не зависит от ее положения в своей плоскости. Следствие 2. Не изменяя действия данной пары на тело, можно менять модули сил и плечо данной пары, но при условии, что ее момент и направление вращения остаются неизменными. Следствие 3. Две данные пары всегда можно привести к одному плечу.
Момент пары как вектор. Понятием алгебраического момента пары удобно пользоваться, если все пары лежат в одной плоскости. Теперь представим, что требуется рассмотреть пары, плоскости действия которых, по отношению друг к другу, расположены в пространстве. В этом случае вводится понятие векторного момента пары. По аналогии с векторным моментом силы относительно центра, векторный момент пары должен определять: - плоскость действия данной пары; - направление вращения пары в этой плоскости; - численное значение момента пары.
Таким образом, модуль этого вектора должен выражать в произвольно выбранном масштабе численное значение момента пары, а направление этого вектора должно определять направление перпендикуляра к плоскости действия пары. Принято направлять векторный момент пары по перпендикуляру к ее плоскости в ту сторону, чтобы, смотря с его конца на пару, 20 видеть эту пару вращающей тело против хода часовой стрелки (рис. 23).
Исходя из того, что действие пары на тело не зависит от ее положения в своей плоскости действия, точка приложения векторного момента пары значения не имеет. Условно, за эту точку принимают середину отрезка, соединяющего точки приложения сил данной пары. Распределенные нагрузки. На практике часто вместо сосредоточенных сил сталкиваются с нагрузками, распределенными по поверхностям по тому или иному закону. В этом случае вводится понятие интенсивности распределенной нагрузки 1. Равномерно – распределенная нагрузка вдоль отрезка прямой В этом случае силы, равномерно распределены вдоль отрезка прямой
Применяя это правило к схеме показанной на рисунке 29 получаем, что 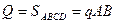 и проходит эта сила через центр тяжести прямоугольника и проходит эта сила через центр тяжести прямоугольника 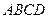 , т.е. через точку пересечения диагоналей и делит сторону , т.е. через точку пересечения диагоналей и делит сторону 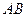 пополам. пополам.
2. Нагрузка, распределенная вдоль отрезка по линейному закону. В этом случае силы, распределены вдоль отрезка прямой 3. Нагрузка, распределенная вдоль отрезка прямой по произвольному закону.
Первую часть задачи, т.е. определения модуля силы 26 31а на ряд бесконечно малых прямоугольников длиной Теперь переходим ко второй части задачи, т.е. определяем точку приложения этой силы. Для этого воспользуемся теоремой Вариньона. Применительно к данным схемам она будет выглядеть следующим образом: 4. Нагрузка, равномерно распределенная по дуге окружности.
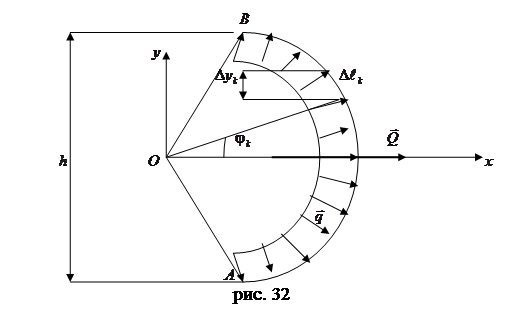
Примером такой нагрузки могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда (рис. 32).
Из симметрии видно, что сумма проекций этих сил на ось 27
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.
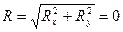 , , 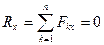 , , 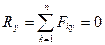 , , 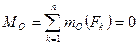 . Тогда . Тогда
2. Вторая форма условий равновесия произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно каких - нибудь двух центров 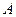 и и 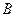 и сумма проекций этих сил на ось и сумма проекций этих сил на ось 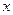 , не перпендикулярную , не перпендикулярную 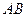 , были равны нулю. , были равны нулю.
Эта форма записи содержит ограничение, чтобыось 28 проекция равнодействующей на эту ось будет равна нулю. Следовательно, все условия равновесия выполняются, но система в равновесии не находится. Значит, для того, чтобы «поймать» этот вектор 3. Третья форма условий равновесия произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно каких - нибудь трех центров  , не лежащих на одной линии, были равны нулю. , не лежащих на одной линии, были равны нулю.
Эта форма записи также содержит ограничение, которое объяснялось во второй форме записи.
Тема 9. Кинематика. Кинематика точки. Основные понятия. Кинематико й называется раздел механики, в котором изучаются геометрические свойства движение материальных тел без учета их инертности (массы), а также причин, вызывающих данное движение (сил). Кинематика представляет собой, с одной стороны, введение в динамику, так как здесь вводятся основные понятия и зависимости необходимые для изучения движения тел с учетом действия сил. С другой стороны, методы кинематики имеют и самостоятельное практическое значение, например, при изучении передач движения в механизмах. Под движением в механике понимается изменение с течением времени положения данного тела в пространстве по отношению к другим телам. Для определения положения движущегося тела с тем телом, по отношению к которому изучается движение, жестко связывают какую – нибудь систему осей координат, которую будем называть системой отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к данной системе отсчета находится в покое (этот случай рассматривался в разделе статика). Если же координаты, каких – нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе отсчета находится в движении. Движение тел совершается в пространстве с течением времени. Пространство в механике рассматривается, как трехмерное, а время считается универсальным, т.е. протекающим одинаково во всех системах отсчета. Время является скалярной, непрерывно меняющейся величиной. В задачах кинематики оно принимается за независимую переменную (аргумент), а все остальные величины (координаты, скорости и т.д.) рассматриваются как функции этого аргумента. Кинематику делят на кинематику точки и кинематику системы материальных точек (тела). В кинематике решаются две основные задачи: - первая задача состоит в установлении математических способов задания движения точек или тел; 36 - вторая задача заключается в том, чтобы, зная закон движения данного тела или точки, определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности. Для решения задач кинематики необходимо, чтобы непосредственно был задан или закон движения данного тела или же закон движения, какого – нибудь другого тела, кинематически связанного с данным.
Способы задания движения точки. Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех способов: естественный, координатный, векторный. 1. Естественный способ задания движения точки. Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным. Пусть точка
Тогда положение точки При движении точка Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным способом, необходимо знать: 37 1. Траекторию движения точки; 2. Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета; 3. Закон движения точки вдоль траектории Следует отметить, что величина
2.Координатный способ задания движения точки. В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы осей (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде: При координатном способе задания движения точки, траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории. При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).
38 Положение точки в этом случае будут определять полярный угол 3.Векторный способ задания движения точки. В этом случае положение точки в пространстве определяется только радиусом – вектором, проведенным из начала декартовой системы координат (рис. 43). Уравнение движения в этом случае имеет вид: Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трех скалярных.
Связь между различными способами задания движения. В этом параграфе показано, как можно сделать переход от одного способа задания движения точки к другому. а) Переход от координатного способа задания движения к векторному. Эту связь легко получить, если ввести единичные векторы (орты) осей По зависимости (16), можно сделать переход от координатного способа задания движения к векторному, и наоборот б) Переход от координатного способа задания движения к естественному. Допустим, что движение задано в виде уравнений (14). Известно, что
Кинематика твердого тела Типы опор (связей) 1. Гладкая поверхность. Гладкой будем называть поверхность, трением о которую данного тела в первом приближении можно пренебречь. Эта связь не дает телу перемещаться только по направлению общей нормали к поверхностям соприкасающихся тел в точке их касания (рис. 1). Поэтому реакция
рис. 1 рис.2 2. Гибкая нерастяжимая нить.
рис. 3 рис.4 9 3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром. Осевая линия болта называется осью шарнира. Тело
4. Шаровой (сферический) шарнир и подпятник.
Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. Примерами таких связей служат шаровая пята, с помощью которой прикрепляется фотоаппарат к штативу и подшипник с упором (подпятник) (рис. 5). Реакция 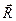 шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее заранее не известны ни модуль реакции шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее заранее не известны ни модуль реакции 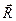 , ни углы, образуемые ею с осями , ни углы, образуемые ею с осями 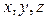 . .
5. Стержень. Пусть в какой-нибудь конструкции связью является стержень
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.35 (0.13 с.) |
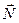 гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис.2), то реакция направлена по нормали к другой поверхности.
гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис.2), то реакция направлена по нормали к другой поверхности.
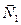
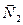
 Гибкой нерастяжимой нитью будем называть такую связь, реакция
Гибкой нерастяжимой нитью будем называть такую связь, реакция  которой направлена вдоль нити к точке ее подвеса (рис. 3). Поскольку нить работает только на растяжение, то реакция нити всегда направлена от данного тела вдоль самой нити.
которой направлена вдоль нити к точке ее подвеса (рис. 3). Поскольку нить работает только на растяжение, то реакция нити всегда направлена от данного тела вдоль самой нити.
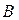
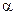
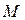
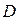
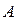

 , прикрепленное шарниром к опоре
, прикрепленное шарниром к опоре 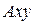 . В этом случае модуль и направление реакции
. В этом случае модуль и направление реакции 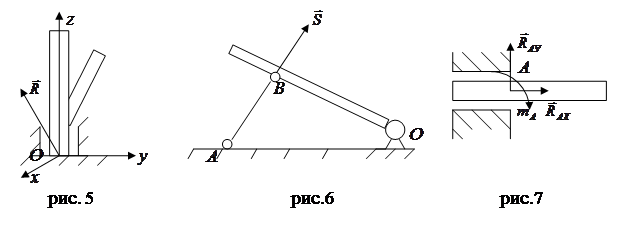
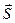 стержня будет направлена вдоль оси стержня.
стержня будет направлена вдоль оси стержня.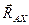 ,
, 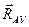 и опорный момент (рис. 7).
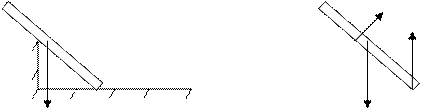
и опорный момент (рис. 7).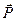 (рис. 8а), для которого связями являются гладкая плоскость
(рис. 8а), для которого связями являются гладкая плоскость 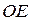 и опора
и опора 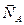 ,
, 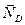 .
.

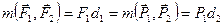 (рис. 22а). Требуется доказать, что эти пары эквивалентны.
(рис. 22а). Требуется доказать, что эти пары эквивалентны.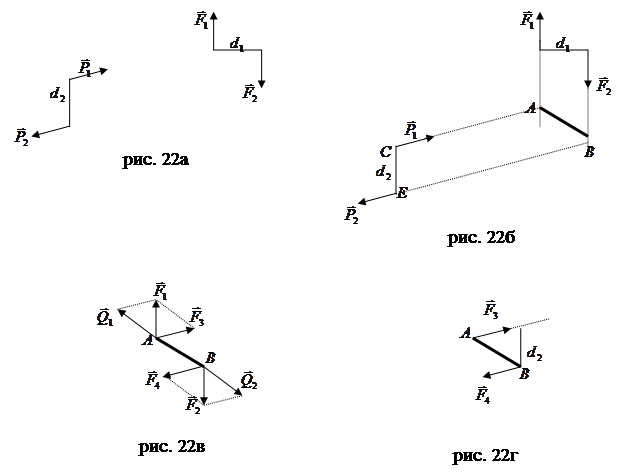
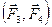 будет численно равен моменту первоначальной пары
будет численно равен моменту первоначальной пары 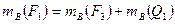 , причем
, причем 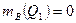 , т.к. линия действия силы
, т.к. линия действия силы 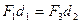 или
или 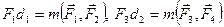 . Тогда учитывая начальные условия, получаем:
. Тогда учитывая начальные условия, получаем: 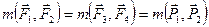 . Учитывая, что у пар
. Учитывая, что у пар 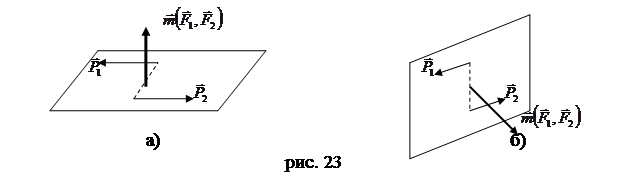
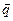 . В зависимости от того, по какой поверхности распределены силы, интенсивность
. В зависимости от того, по какой поверхности распределены силы, интенсивность 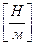 ,
,  ,
, 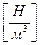 . Рассмотрим нагрузку, распределенную по длине для различных случаев.
. Рассмотрим нагрузку, распределенную по длине для различных случаев.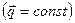 .
. (рис. 29). Общее правило замены распределенной нагрузки сосредоточенной силой: модуль сосредоточенной силы
(рис. 29). Общее правило замены распределенной нагрузки сосредоточенной силой: модуль сосредоточенной силы 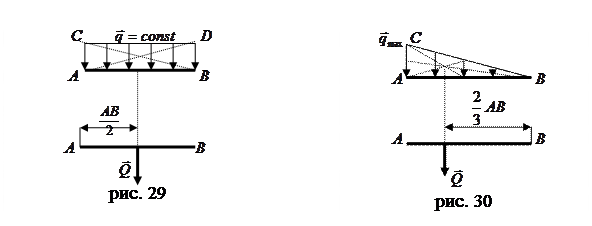
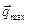 (рис. 30). Примером такой нагрузки могут служить силы давления воды, распределенные по высоте какого – либо не полностью погруженного тела. Действуя по процедуре описанной выше, также заменяем эту распределенную нагрузку сосредоточенной силой
(рис. 30). Примером такой нагрузки могут служить силы давления воды, распределенные по высоте какого – либо не полностью погруженного тела. Действуя по процедуре описанной выше, также заменяем эту распределенную нагрузку сосредоточенной силой 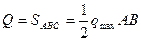 и проходит эта сила через центр тяжести треугольника
и проходит эта сила через центр тяжести треугольника  , т.е. через точку пересечения медиан и делит высоту
, т.е. через точку пересечения медиан и делит высоту 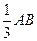 от основания
от основания 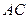 и
и 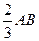 от вершины
от вершины 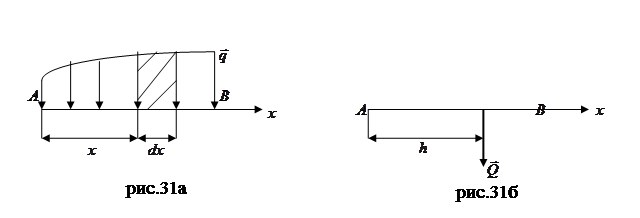
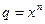 . Покажем, как можно сделать переход от схемы 31а к схеме 31б.
. Покажем, как можно сделать переход от схемы 31а к схеме 31б.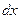 . Модуль сосредоточенной силы от этой элементарной нагрузки будет равен
. Модуль сосредоточенной силы от этой элементарной нагрузки будет равен 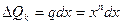 . Переходя от элементарных фигур к фигуре показанной на рисунке 31а берем интеграл по длине
. Переходя от элементарных фигур к фигуре показанной на рисунке 31а берем интеграл по длине 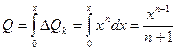 .
.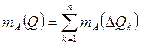 . Разбиваем произвольную фигуру, показанную на рисунке 31а на ряд бесконечно малых прямоугольников длиной
. Разбиваем произвольную фигуру, показанную на рисунке 31а на ряд бесконечно малых прямоугольников длиной 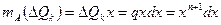 . Тогда
. Тогда 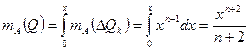 . Но с другой стороны, если посмотреть на рисунок 31б,
. Но с другой стороны, если посмотреть на рисунок 31б, 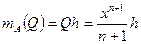 . Приравнивая правые части полученных равенств, получаем выражение для
. Приравнивая правые части полученных равенств, получаем выражение для 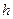 :
: 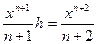 , отсюда
, отсюда 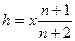 .
.
 равна нулю. Следовательно, их равнодействующая
равна нулю. Следовательно, их равнодействующая 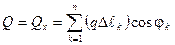 , где
, где 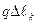 - сила, действующая на элемент дуги длиной
- сила, действующая на элемент дуги длиной 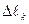 ,
, 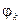 - угол, образуемой этой силой с осью х. Из рисунка видно, что
- угол, образуемой этой силой с осью х. Из рисунка видно, что 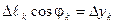 , тогда, вынося общий сомножитель
, тогда, вынося общий сомножитель 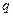 за знак суммы, получаем:
за знак суммы, получаем: 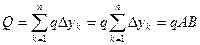 . Окончательно
. Окончательно 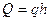 , где
, где  .
.

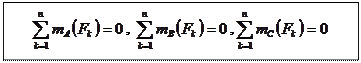
 движется относительно системы отсчета, вдоль некоторой траектории
движется относительно системы отсчета, вдоль некоторой траектории 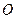 , которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.
, которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.
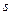 , равной расстоянию от точки
, равной расстоянию от точки 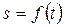 (13)
(13)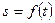 .
. 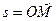 , а пройденный за это время движения путь будет равен
, а пройденный за это время движения путь будет равен 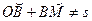 .
.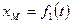 ,
, 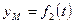 ,
, 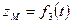 (14)
(14)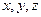 , которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.
, которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.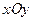 , получаем два уравнения движения
, получаем два уравнения движения 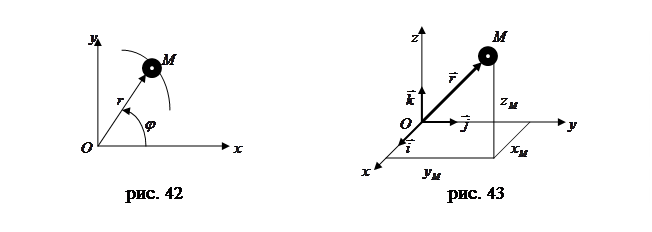
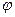 и вектор
и вектор 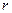 , т.е. уравнения движения точки в полярных координатах имеют вид:
, т.е. уравнения движения точки в полярных координатах имеют вид: 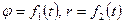 .
.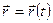 (15)
(15)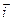 ,
, 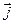 ,
, 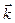 (рис. 43). Тогда учитывая, что проекции вектора
(рис. 43). Тогда учитывая, что проекции вектора 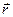 на оси
на оси 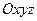 равны координатам точки
равны координатам точки 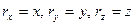 , получаем:
, получаем: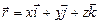 (16)
(16)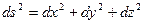 или
или 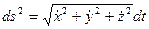 , где
, где 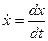 ,
, 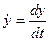 ,
, 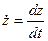 . Отсюда получаем:
. Отсюда получаем: 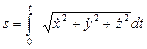 (17)
(17)


