Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о сложении вероятностей.
Вероятность суммы совместных событий вычисляется по формуле:
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный. Решение. Обозначим события: А – вынули белый шар из первого ящика,
В – белый шар из второго ящика,
Нам нужно, чтобы произошло одно из событий
Пусть
Формула Байеса Пусть
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. Решение. Возможны три гипотезы:
Так как вызов на линию огня любого стрелка равновозможен, то
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность гипотезы
Практическое занятие №4 1 Наименование работы: Вычисление вероятностей по формуле Бернулли и формулам Лапласа. 2 Цель работы: применение теоретических знаний к решению задач.
Формирование ОК 2,3,5,6,8; овладение знаниями и умениями, необходимыми для освоения ПК 1.2. (спец. 09.02.03.), ПК 1.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Формулы Бернулли и Лапласа». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №4. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: 1. Пусть вероятность того, что ноутбук потребует ремонта в течение гарантийного срока, равна 0,22. Найти вероятность того, что в течение гарантийного срока из 7 ноутбуков: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта. 2. Среди деталей, обрабатываемых рабочим, бывает в среднем 5% нестандартных. Найти вероятность того, что среди взятых на испытание 32 деталей четыре будут нестандартными. 3. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: а) герб выпадет три раза; б) герб выпадет один раз; в) решка выпадет 4 раза. 4. Два равносильных противника играют в шахматы. Выиграть две партии из четырех, или три партии из пяти? 5. В игре разыгрывают 4 автомобиля за 4 дня. Всего участвует 100 человек. Какова вероятность выигрыша сразу трех автомобилей одним человеком? Ответ выразите в процентах. 6. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов. 7. Магазин получил 1000 бутылок шампанского. Вероятность того, что при перевозке бутылка разобьется, равна 0,01. а) Найти вероятность того, что магазин получит ровно 5 разбитых бутылок. б) Найти вероятность того, что все бутылки прибудут в магазин целыми. 8. Известно, что при контроле бракуется 5 % изготовленных компьютерных столов. Для контроля отобрано 545 изделий. Какова вероятность того, что среди отобранных деталей не менее 500 и не более 520 столов отличного качества. 9. В среднем, в России, на 100 браков приходится 11 разводов. Найдите вероятность того, что среди 1000 брачующихся не менее 210 и не более 340 разведутся.
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.9) и сдайте зачет). 8 Содержание отчета: Решения задач в соответствии с заданием.
9 Контрольные вопросы: 1. Что называется схемой Бернулли? 2. Приведите примеры повторных испытаний. 3. Запишите теорему Бернулли. 4. Сформулируйте теорему Муавра – Лапласа 5. Запишите интегральную теорему Муавра - Лапласа ПРИЛОЖЕНИЕ: Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p = P (A), а вероятность противоположного события (событие А не наступило) - буквой q = P ( Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли
Распределение числа успехов (появлений события) носит название биномиального распределения. Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых. Решение. Событие А – достали белый шар. Тогда вероятности
Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико, а число p отлично от 0 и 1, тогда:
Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться
Пример: Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества. Решение. По условию n=400, p=0.75, q=0.25, k=280, откуда
По таблицам найдем Искомая вероятность равна:
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.45 (0.014 с.) |
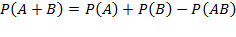 .
.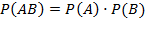
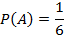
 - вынули черный шар из первого ящика,
- вынули черный шар из первого ящика,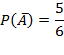
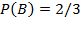
 - черный шар из второго ящика,
- черный шар из второго ящика,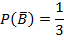
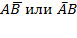 . По теореме об умножении вероятностей
. По теореме об умножении вероятностей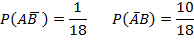 Тогда искомая вероятность по теореме сложения будет
Тогда искомая вероятность по теореме сложения будет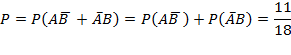 Формула полной вероятности
Формула полной вероятности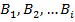 — полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле:
— полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле: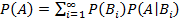
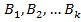 — полная группа событий и A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие
— полная группа событий и A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие 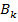 , если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:
, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле: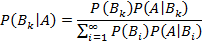
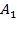 - на линию огня вызван первый стрелок,
- на линию огня вызван первый стрелок,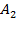 - на линию огня вызван второй стрелок,
- на линию огня вызван второй стрелок,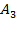 - на линию огня вызван третий стрелок.
- на линию огня вызван третий стрелок.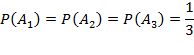
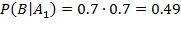
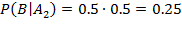
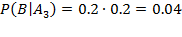
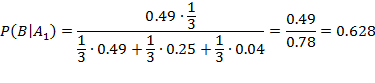
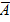 )=1− p.
)=1− p.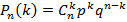
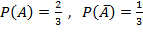
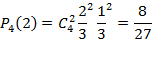
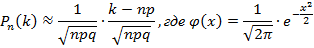
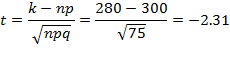
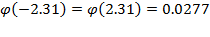 .
.