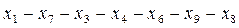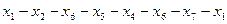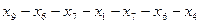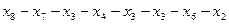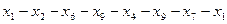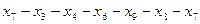Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметромλ>0, если функция плотности распределения вероятностей имеет вид:
0 при х<0, f(х)= λе-λх при х≥0.
Функция распределения случайной величины Х, распределенной по показательному закону, задается формулой:
F(х)= 1-e-λх при х≥0.
Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:
M(X)=
Вероятность попадания Х в интервал (a;b) вычисляется по формуле: Р(a<Х<b)= e-λа- e-λb
Пример 2. Среднее время безотказной работы прибора равно 100 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) плотность распределения вероятностей; б) функцию распределения; в) вероятность того, что время безотказной работы прибора превысит 120 ч.
Решение: По условию математическое распределение M(X)= Следовательно,
а) f(х)= 0,01е -0,01х при х≥0.
б) F(x)= 0 при х<0, 1- е -0,01х при х≥0.
в) Искомую вероятность найдем, используя функцию распределения: Р(X>120)=1-F(120)=1-(1- е -1,2)= е -1,2≈0,3.
Практическое занятие №8 1 Наименование работы: Построение для заданной выборки ее графической гистограммы, расчет ее числовых характеристик. 2 Цель работы: отработать навык решения задач по математической статистике. Формирование ОК 2,3,4, 8; овладение знаниями и умениями, необходимыми для освоения ПК 3.4. (спец. 09.02.03.), ПК 1.1, 1.2, 1.4, 2.3. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Математическая статистика». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №8. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: 1. Дан статистический ряд распределения частот. Составьте ряд распределения относительных частот, найдите медиану, моду вариационного ряда и среднеарифметическое значение. Постройте полигон частот и относительных частот для двух различных вариационных рядов.
2. Постройте гистограмму частот и относительных частот:
3. Андрей написал 6 программ для 6 одногруппников.1-ая программа содержит 3 ошибки, 2-ая - 8 ошибок, 3-я - 5 ошибок, 4-ая - 3 ошибки, 5-ая - 1 ошибку, 6-ая - 7 ошибок. Составьте ряд распределения частот и относительных частот, найдите медиану, моду вариационного ряда и среднеарифметическое значение. Постройте полигон частот и относительных частот. 4. Возраст работников предприятия в техническом отделе представлен следующим вариационным рядом: 18, 22, 30, 30, 32, 44, 45, 22, 18, 24, 25, 44, 32, 22, 18, 32, 44, 18, 22, 18, 22, 30, 30, 30, 25, 25, 20. Составьте ряд распределения частот и относительных частот, найдите медиану, моду вариационного ряда и среднеарифметическое значение. 5. В магазин телефонов поступили Iphone следующих моделей 4s, 5, se, 6, 6plus, 6s, 6s plus, 7plus, 8 plus, X, 5s, 6plus, 7,5s, 6plus, X, 5s, 5, 4s, se, X, 4s, 5, 5s, 5s, 6plus, 5s, 4s, X, se, X, 4s, 6plus, X,7, se, 8 plus, 4s, X, 6plus, X, 6s plus, 7, 6s plus, 4s, 7, 6s plus, 4s, se, 5, 4s, se, X,, 6s,, 6s, 8 plus, 8 plus, 6s, 6s plus, 7, 8 plus,7, X, 5s, 6plus, 7,5s, 6plus, X, 5s, 5, 4s, se, X, 4s, 5, 5s, 5s, 6plus, 5s, 4s, X, se, X, 4s, 6plus, X,7, se, 8 plus, 4s, X, se, 8 plus, 4s, X, 6plus, X, 6s plus, 7, 6s plus. Составьте интегральный ряд распределения частот и относительных частот.
Контрольные вопросы: 1. Что называется статистическим рядом? 2. Что называется медианой, модой и средним арифметическим значением вариационного ряда? 3. Что называется полигоном частот и относительных частот? 4. Что называется гистограммой частот и относительных частот?
ПРИЛОЖЕНИЕ
Пусть проводится n - независимых испытаний, в результате которых получено n — значений СВ х1>х2,..., хn. Совокупностью этих значений называется выборочной статистической совокупностью. Множество элементов, у которых была произведена выборка, называется генеральной совокупностью, (множество всех молекул кислорода, содержащихся в данной аудитории, множество рыб в водоеме, всё население нашей страны). При этом х называется вариантами совокупности, n — объем совокупности.
Варианты обычно располагаются либо в порядке возрастания, либо в порядке убывания и записываются по порядку.
Статистическим рядом называется ряд вариантов, расположенных либо в порядке возрастания, либо в порядке убывания, с соответствующим или частотами. Например, дана выборка: 1,3; 1,8; 1,2; 3,0; 2,1; 5; 2,4; 1,2; 3,2;1,2; 4; 2,4. Это ряд вариантов. Расположив эти варианты в возрастающем порядке, мы получим вариационный ряд: 1,2; 1,2; 1,2; 1,3; 1,8; 2,1; 2,4; 2,4; 3,0; 3,2; 4; 5. Разность между максимальным и минимальным значениями элементов выборки называется размахом выборки. R= x max− x min Размах представленной выборки составляет 3,8 Медианой вариационного ряда называется то значение случайной величины, которое приходится на средину вариационного ряда (Ме). Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине. Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда. Сосчитаем число членов, их 12 - чётное число членов, значит надо найти среднее арифметическое двух чисел записанных посередине, то есть 6 и 7-ой варианты. (2,1+2,4)\2=2.25 – медиана. Модой вариационного ряда называют вариант (значение случайной величины), которому соответствует наибольшая частота (Мо), т.е. которая встречается чаще других. Модой является 1.2, т.к. только это число встречается 3 раза, а остальные встречаются меньше, чем 3 раза. Среднеарифметическим значением вариационного ряда называется результат деления суммы значений статистической переменной на число этих значений, то есть на число слагаемых. Правило нахождения среднеарифметического значения выборки: 1. каждую варианту умножить на её частоту (кратность); 2. сложить все полученные произведения; 3. поделить найденную сумму на сумму всех частот. Среднеарифметическое значение находим так: (1,2*3+1,3+1,8+2,1+2,4*2+3,0+3,2 +4+5)\12=2,4 Составим вариационный ряд:
Частота Относительная частота wi это отношение i-ой частоты к объему всей совокупности, т.е Для построения интервального ряда необходимо: 1. определить величину частичных интервалов; 2. определить ширину интервалов; 3. установить для каждого интервала его верхнюю и нижнюю границы; 4. сгруппировать результаты наблюдении. Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном случае исходя из целей исследования, объема выборки и степени варьирования признака в выборке. Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов h вычисляют: 1) Rразмах = xmax – xmin 2) Приблизительно число интервалов k можно оценить исходя только из объема выборки n 3) Нижняя граница первого интервала x1 выбирается так, чтобы минимальная варианта выборки xmin попадала примерно в середину этого интервала: xh1 = xmin - 0,5·h. Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h:
xhi = xhi-1 +h. Построение шкалы интервалов на основе вычисления границ интервалов продолжается до тех пор, пока величина xhi удовлетворяет соотношению: xhi < xmax + 0,5·h. В соответствии со шкалой интервалов производится группирование значений признака - для каждого частичного интервала вычисляется сумма частот ni вариант, попавших в i -й интервал. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы интервала.
Пусть нам дан ряд распределения, записанный с помощью таблицы:
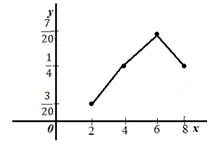
Полигон частот - ломанная, которая соединяет точки (xn, mn). То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной. Полигон относительных частот - ломанная, которая соединяет точки (xn, wn). То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной: Пример: Пусть распределение имеет вид:
Полигон частот
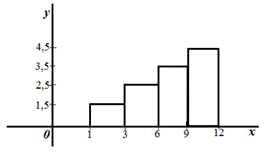
В случае непрерывного признака целесообразно строить гистограмму. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению mi / h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии mi / h Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2). Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. Дан ряд непрерывного распределения частот:
Построить гистограмму частот
Очевидно, что в данном случае длина частичного интервала h=2. Найдем высоты прямоугольников каждой точки разбиения. При х=3; При х=6; При х=9;
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот. Решение. 1) Статистический ряд распределения частот:
2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Напишем распределение относительных частот:
Контроль: 0,1+0,2+0,4+0,1+0,2=1. Полигоном частот называют ломаную, отрезки, которой соединяют точки (х1,m1),(х2,m2),...,(хk,mk). Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты mi. Точки (хi,mi) соединяют отрезками и получают полигон частот. Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х1,w1),(х2,w2),...,(хk,wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки (хi,wi) соединяют отрезками и получают полигон относительных частот. Пример 2. Постройте полигон частот и относительных частот по данным примера 1.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно (или невозможно) учитывать, то варианты группируются в интервалы. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Часто hi-hi-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и hi: 1. Rразмах=Xmax-Xmin Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:
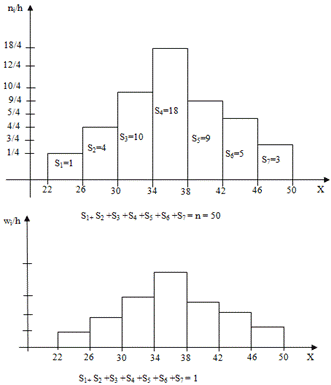
Пример 3. Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.
Решение. Определим характеристики группировки с помощью замечания.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.
Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки. Практическое занятие №9 1 Наименование работы: Способы задания графов. Характеристики графов. 2 Цель работы: научиться применять понятийный аппарат к решению практических задачи по теории графов. Формирование ОК 1,2,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 3.4. (спец. 09.02.03.), ПК 1.1. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Теория графов». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №9. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие:
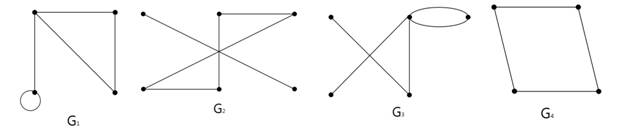
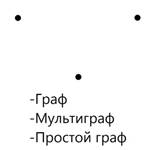
1. Перечислите мультиграфы, простые графы, двудольные и полные графы. Назовите порядок каждого графа.
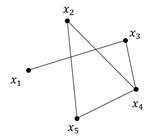
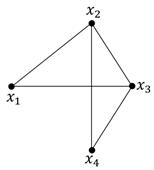
2. Найти степень вершин графа. Присутствуют ли у него висячие и изолированные вершины?
3. Найти полустепени исхода и захода для каждой из вершин графа. Присутствуют ли у него висячие и изолированные вершины?
4. Постройте для данных графов матрицы смежности вершин и дуг, матрицы инцидентности.
5.
6. Выполните следующие задания: 1) 2) Найти расстояние между вершинами 1 и 7, 2 и 5, 3 и 4, 2 и 4. 3) Найти эксцентриситеты всех вершин. 4) Определите диаметр и центр графа. Запишите номера переферийных вершин. 5) Определите центр графа. 7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.6) и сдайте зачет). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1. Что называется графом? 2. Какой граф называется ориентированным? 3. Какие графы называются мультиграфом, простым графом и двудольным? 4. Степени вершин графа. 5. Способы задания графов? 6. Что такое маршрут, путь и контур? 7. Опишите метрические характеристики графа. ПРИЛОЖЕНИЕ: Графом называется набор точек (эти точки называются вершинами), некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами). Обозначение: G=(S,U), где S- множество вершин графа, U- множество ребер. Число вершин графа G=(S,U) называется его порядком. Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Этоозначает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой). Мультиграфом называется граф без петель. Простым графом называется мультиграф без кратных ребер. Неориентированный граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям (если его вершины можно правильно покрасить в два цвета).
Степени вершин графа. Число ребер графа G, инцидентных данной вершине Вершина называется изолированной, если ее степень равна нулю. Вершина называется висячей, если ее степень равна единице. Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой. Полустепенью исхода (захода) вершины
Способы задания графа. 1. Перечислением вершин и ребер.
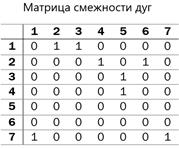
2. Графическим способом с помощью диаграммы. Матричным способом. 1) Матрицей смежности вершин графа G=(S,U) порядка n называется квадратная матрица порядка n, строки и столбцы которой соответствуют вершинам графа, где элементы 2) Матрицей смежности дуг графа G=(S,U),где
Пример 3: Для данного графа построить матрицы смежности вершин и дуг.
Маршруты, цепи и циклы. Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней. Путь (простая цепь) в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер). Контур (простой цикл) – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней. Пример 4:
Пример замкнутого маршрута:
Пример цепи:
Пример пути (простой цепи):
Пример цикла:
Пример контура (простого цикла):
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.233.41 (0.149 с.) |

 0 при х≤3,
0 при х≤3, , D(X)=
, D(X)= 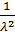 , σ (Х)=
, σ (Х)= 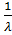
 0 при х<0,
0 при х<0,
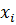
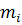
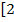 ;7)
;7)
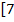 ;12)
;12)
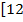 ;17)
;17)
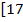 ;22)
;22)
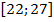
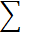
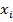
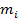
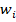 =
= 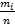
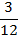
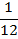
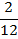
 =
= 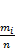 . Причем
. Причем 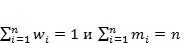
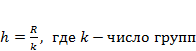
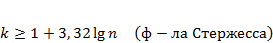
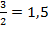
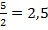
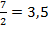
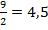
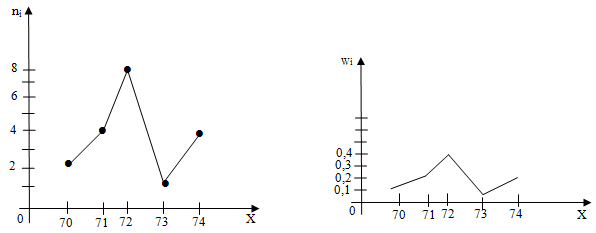
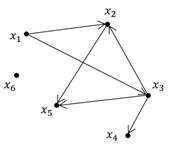
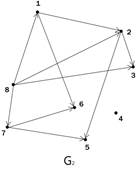
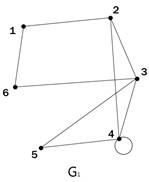
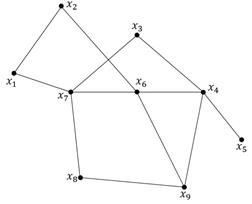
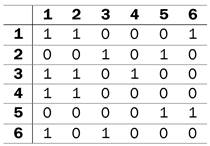 По заданной матрице вершин постройте граф, затем, произвольно пронумеруйте дуги и постройте для своего графа матрицу дуг.
По заданной матрице вершин постройте граф, затем, произвольно пронумеруйте дуги и постройте для своего графа матрицу дуг.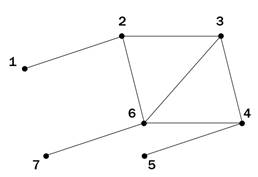 Для данного графа запишите пример незамкнутого маршрута, замкнутой цепи, простой цепи, цикла и контура.
Для данного графа запишите пример незамкнутого маршрута, замкнутой цепи, простой цепи, цикла и контура.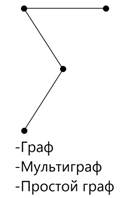
 Пример 1:
Пример 1: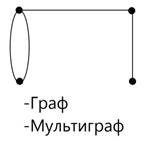
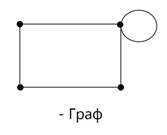
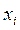 называется степенью (валентностью) данной вершины и обозначается
называется степенью (валентностью) данной вершины и обозначается 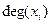 .
.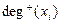 (
(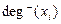 ) его дуг, исходящих из вершины
) его дуг, исходящих из вершины 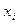 (заходящих в вершину
(заходящих в вершину 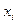 )
) Пример 2:
Пример 2: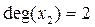
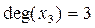
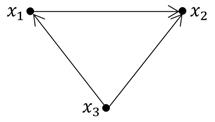
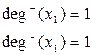
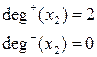
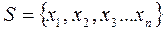
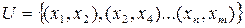
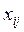 равны числу дуг, идущих из i-ой вершины, в j-ую.
равны числу дуг, идущих из i-ой вершины, в j-ую.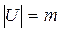 , называется квадратная матрица, порядка m, элементы которой
, называется квадратная матрица, порядка m, элементы которой 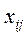 равны единице, если дуга
равны единице, если дуга 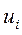 непосредственно предшествует дуге
непосредственно предшествует дуге 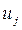 , и равны нулю в остальных случаях.
, и равны нулю в остальных случаях.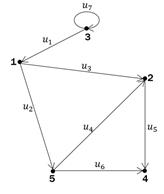 3) Матрица инцидентности - одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.
3) Матрица инцидентности - одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.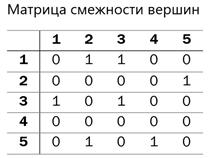
 Пример незамкнутого маршрута:
Пример незамкнутого маршрута: