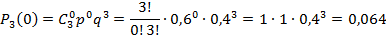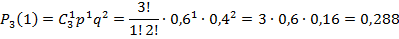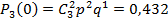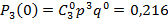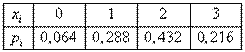Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
где
Практическое занятие №5 1 Наименование работы: Закон распределения ДСВ. Вычисление характеристик ДСВ. 2 Цель работы: применение теоретических знаний к решению задач. Формирование ОК 1,2,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 1.1, 1.2. (спец. 09.02.03.), ПК 1.2, 2.3. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Характеристики ДСВ». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №5. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: 1. Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение, а также, построить многоугольник распределения дискретной случайной величины Х, заданной законом распределения:
2. Дискретная случайная величина Х имеет закон распределения:
Найти вероятность р1 и р3, если известно, что р3 в четыре раза больше р1. Построить многоугольник распределения. 3. Составить закон распределения вероятностей случайной величины числа очков, выпавшего на верхней грани игрального кубика при двух подбрасываниях, если известно, что в сумме выпало 6 очков. 4. В билете 2 задачи. Вероятность правильного решения первой задачи- 0,9, а второй- 0,65. Случайная величина Х- число правильно решенных задач в билете. Составить закон распределения, вычислить математическое ожидание, дисперсию и среднее математическое отклонение этой случайной величины. 5. На карточках написаны буквы, всего 3 согласных и 4 гласных. Наугад выбирают 3 карточки, причем каждый раз взятую карточку возвращают назад. Случайная величина Х- число гласных букв среди взятых карточек. Составить закон распределения и найти М(Х), D(X) и σ(X). 6. В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не отыщется подходящий ключ. Построить закон распределения для случайной величины x – числа опробованных ключей. Построить функцию распределения Fx(x) для случайной величины x 7 Порядок выполнения работы:
Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.6) и сдайте зачет). 8 Содержание отчета: Решения задач в соответствии с заданием. 9 Контрольные вопросы: 1. Что называется случайной величиной? Виды случайных величин. 2. Что называется законом распределения ДСВ? 3. Как проверить правильность составления закона ДСВ? 4. Перечислите характеристики ДСВ. 5. Что называется математическим ожиданием ДСВ? Перечислите его свойства. 6. Что называется дисперсией ДСВ? Перечислите ее свойства. 7. Что называется средним квадратическим отклонением ДСВ?
ПРИЛОЖЕНИЕ: Случайной называется величина, которая в результате испытания принимает только одно значение из возможного множества своих значение, наперед неизвестное и зависящее от случайных причин. Различают два вида случайных величин: дискретные и непрерывные. Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное. Другими словами, возможные значения дискретной случайной величину можно перенумеровать. Описать случайную величину можно с помощью ее закона распределения. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями. Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, в первой строке которой указаны в порядке возрастания все возможные значения случайной величины, а во второй строке соответствующие вероятности этих значений, т.е.
где р1+ р2+…+ рn=1 Такая таблица называется рядом распределения дискретной случайной величины. Если множество возможных значений случайной величины бесконечно, то ряд р1+ р2+…+ рn+… сходится и его сумма равна 1. Пример 1. Вероятности того, что студент сдаст экзамен в сессию по математическому анализу и органической химии соответственно равны 0,7 и 0,8. Составить закон распределения случайной величины Х- числа экзаменов, которые сдаст студент. Решение. Рассматриваемая случайная величина X в результате экзамена может принять одно из следующих значений:x1=0, x2=1, х3=2.
Найдем вероятность этих значений.Обозначим события: А- «студент сдаст экзамен по математическому анализу»
В - «студент сдаст экзамен по органической химии»
По условию:
Тогда:
Итак, закон распределения случайной величины Х задается таблицей:
Контроль:0,6+0,38+0,56=1. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности: М(Х) = ∑ xiрi= x1р1 + x2р2+…+ xnрn i=1 Математическое ожидание служит характеристикой среднего значения случайной величины. Свойства математического ожидания: 1)M(C)=C, где С-постоянная величина; 2)М(С•Х)=С•М(Х), 3)М(Х±Y)=М(Х) ±M(Y); 4)M(X•Y)=M(X) •M(Y), где X,Y- независимые случайные величины; 5)M(X±C)=M(X)±C, где С-постоянная величина; Для характеристики степени рассеивания возможных значений дискретной случайной величины вокруг ее среднего значения служит дисперсия. Дисперсией D (X) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X)=M(X-M(X))2 Свойства дисперсии: 1)D(C)=0, где С-постоянная величина; 2)D(X)>0, где Х- случайная величина; 3)D(C•X)=C2•D(X), где С-постоянная величина; 4)D(X+Y)=D(X)+D(Y), где X,Y- независимые случайные величины; Для вычисления дисперсии часто бывает удобно пользоваться формулой: D(X)=M(X2)-(M(X))2, n где М(Х)=∑ xi2рi= x12р1 + x22р2+…+ xn2рn i=1
Средним квадратическим отклонением
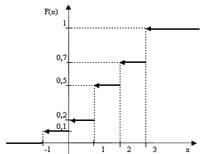
Пример 2. Дискретная случайная величина Х задана законом распределения:
Найти Р2, функцию распределения F(x) и построить ее график, а также M(X),D(X), σ(Х). Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то Р2=1- (0,1+0,3+0,2+0,3)=0,1 Найдем функцию распределения F(х)=P(X<x). Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Если х≤-1, то F(х)=0, т.к. на (-∞;х) нет ни одного значения данной случайной величины; Если -1<х≤0, то F(х)=Р(Х=-1)=0,1, т.к. в промежуток (-∞;х) попадает только одно значение x1=-1; Если 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т.к. в промежуток (-∞;х) попадают два значения x1=-1 и x2=0; Если 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т.к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Если 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т.к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Если х>3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)+Р(Х=3)= 0,1+0,1+0,3+0,2+0,3=1, т.к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1,х4=2 и х5=3.
Итак, 0 при х≤-1, 0,1 при -1<х≤0, 0,2 при 0<х≤1, F(x)= 0,5 при 1<х≤2, 0,7 при 2<х≤3, 1 при х>3
Изобразим функцию F(x)графически (рис.3):
рис. 3 Найдем числовые характеристики случайной величины: n М(Х) = ∑ xκрκ =x1р1 + x2р2+…+ xnрn κ=1 M(X)=-1•0,1+0•0,1+1•0,3+2•0,2+3•0,3=1,5 n D(X)= ∑ x2κрκ –(M(X))2 = x21р1 + x22р2+…+ x2nрn –(M(X))2 κ=1 D(X)=(-1)2 •0,1+12•3+22•0,2+32•0,3-(1,5)2=1,65
Практическое занятие №6 1 Наименование работы: Функция распределения и плотность распределения НСВ. Вычисление характеристик НСВ. 2 Цель работы: отработать навык решения задач. Формирование ОК 1, 3-5,8; овладение знаниями и умениями, необходимыми для освоения ПК 1.1, 1.2. (спец. 09.02.03.), ПК 1.2, 1.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Характеристики НСВ». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №6. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: 1. F(x)= Найти: 1)c 2)M(x),D(x), 2. f(x)= Найти: 1)M(x),D(x), 3. f(x)= Найти: 1)с 2)F(x)
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.3) и сдайте зачет). 8 Содержание отчета: Решения задач в соответствии с заданием.
9 Контрольные вопросы: 1. Какую величину называют непрерывной? 2. Плотность распределения вероятностей и ее гафик. 3. Числовые характеристики НСВ.
ПРИЛОЖЕНИЕ: Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси. Функцией распределения непрерывной случайной величины Х называется функция F(х), определяющая для каждого значения х вероятность того, что случайная величины Х в результате испытания примет значение, меньшее х: F(x)=P(X<x),где х Плотностью распределения вероятностей f (x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.: f(x)=F’(x) Графикплотности распределения вероятностей f(x) называется кривой распределения вероятностей.
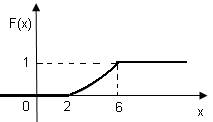
0 при х≤2, f(x)= с(х-2) при 2<х≤6, 0 при х>6. Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в) Р(3≤х<5)
∫ f(x)dx=∫ 0dx+ ∫ c(х-2)dx +∫ 0dx= c∫ (х-2)dx=с(х2/2-2х) =с(36/2-12-(4/2-4))=8с; -∞ -∞ 2 6 2 2 8с=1; с=1/8. х б) Известно, что F(x)= ∫ f(x)dx -∞
Поэтому, х если х≤2, то F(x)= ∫ 0dx=0;
если 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х- (4/2-4))= -∞ -∞ 2 =1/8(х2/2-2х+2)=1/16(х-2)2;
если х>6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx+∫ 0dx=1/8∫(х-2)dx=1/8(х2/2-2х) = -∞ 6 2 2 2 =1/8(36/2-12-(4/2+4))=1/8•8=1. Таким образом,
F(х)= (х-2)2/16 при 2<х≤6, 1 при х>6.
График функции F(х) изображен на рис.
в) Р(3≤Х<5)=F(5)-F(3)=(5-2)2/16-(3-2)2/16=9/16-1/16=5/16. Пример 2. Случайная величина Х задана функцией распределения:
0 при х≤0, F(х)= (3• arctg х)/π при 0<х≤√3, 1 при х>√3.
Найти дифференциальную функцию распределения f(х)
Решение: Т.к.f(х)= F’(x), то
0 при х≤0, f(х)= (3•(1+х2)) /π при 0<х≤√3, 0 при х>√3.
Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством: +∞ M(X)= ∫ x•f(x)dx, -∞ при условии, что этот интеграл сходится абсолютно. Дисперсия D (X) непрерывной случайной величины Х определяется равенством: +∞ D(X)= ∫ (х-М(х)2)•f(x)dx, или -∞ +∞ D(X)= ∫ х2•f(x)dx- (М(х))2 -∞ Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством:
Практическое занятие №7 1 Наименование работы: Виды распределений ДСВ и НСВ. 2 Цель работы: применение теоретических знаний к решению задач.
Формирование ОК 1,2,4,5; овладение знаниями и умениями, необходимыми для освоения ПК 2.4, 3.4. (спец. 09.02.03.), ПК 1.1, 1.2, 1.4. (спец. 09.02.04.). 3 Подготовка к занятию: Повторите тему: «Виды распределений ДСВ и НСВ». 4 Литература: 4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018. 4.2 Приложение к ПЗ №7. 5 Перечень необходимого оборудования и материалов: 5.1 Бланк для отчета. 5.2 Канцелярские принадлежности. 6 Задание на занятие: 1. В магазин привозят телевизоры, произведенные в Китае (40% от всех привезенных телевизоров) и произведенные в Корее. Куплено 4 телевизора. Найти закон распределения числа купленных телевизоров, произведенных в Китае. Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины. 2. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных? 3. Студент КС ПГУТИ кидает снежком по мишени до первого попадания. Вероятность попадания в цель при одном бросании постоянна и равна 0,7. Найти вероятность того, что он попадет при четвертом бросании. 4. Игральная кость подбрасывается до первого появления цифры 1. Составьте ряд распределения, найдите функцию распределения и постройте её график. Определить все числовые характеристики, для случайной величины Х числа осуществляемых подбрасываний. 5. Случайная величина Х равномерно распределена в интервале (-3;5). Найдите: а) плотность распределения f(x); б) функции распределения F(x); в) числовые характеристики; г) вероятность Р(4<х<6). 6. Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного функцией распределения:
F(x)= 0, при х<0, 1-е-8х, при х≥0.
7. Непрерывная случайная величина Х задана плотностью распределения вероятностей:
f(x)= 0, при х<0, 0,7•е-0,7х, при х≥0.
а) Назовите закон распределения рассматриваемой случайной величины. б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х.
7 Порядок выполнения работы: Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.7) и сдайте зачет). 8 Содержание отчета: Решения задач в соответствии с заданием.
9 Контрольные вопросы: 1. Биноминальное распределение ДСВ. 2. Геометрическое распределение ДСВ. 3. Равномерный и показательный закон распределение НСВ. ПРИЛОЖЕНИЕ: Биномиальное распределение Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности pi вычисляют по формуле Бернулли.
Для биномиального распределения: Среднее квадратическое отклонение: Пример 1: Построить ряд распределения числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,6. Найти среднее число попаданий и дисперсию. Решение:
Искомый закон распределения:
Контроль: 0,064 + 0,288 + 0,432 + 0,216 = 1
Дисперсия:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.248 (0.145 с.) |
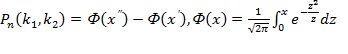 - функция Лапласа.
- функция Лапласа.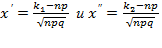
 - «студент не сдаст экзамен по математическому анализу»
- «студент не сдаст экзамен по математическому анализу» - «студент не сдаст экзамен по органической химии»
- «студент не сдаст экзамен по органической химии»
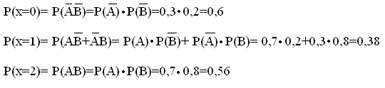
 Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния возможных значений случайной величины используют также величину √D(X).
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния возможных значений случайной величины используют также величину √D(X).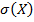 случайной величины Х называется квадратный корень из дисперсии:
случайной величины Х называется квадратный корень из дисперсии: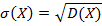
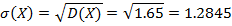
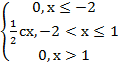
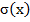
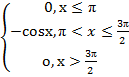
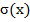
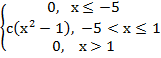
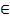 R
R Пример 1. Случайная величина Х задана плотностью распределения вероятностей:
Пример 1. Случайная величина Х задана плотностью распределения вероятностей: +∞ 2 6 +∞ 6 6
+∞ 2 6 +∞ 6 6 -∞ 2 2 х
-∞ 2 2 х 2 6 х 6 6
2 6 х 6 6 0 при х≤2,
0 при х≤2,