Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.2. Плоская система сходящихся сил.Содержание книги
Поиск на нашем сайте
Определение равнодействующей двумя способами. Примеры плоской системы сходящихся сил.
R1 R2 R1 R2 R3 R2 R1 G G G
Существуют два способа нахождения равнодействующей
1. Геометрический способ определения равнодействующей. Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил.(4-я аксиома статики). Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил. Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
F 1 F 4
F 2
F 2 F 3 А В F 1 F 4 D F 3 FΣ О С
FΣ = F1 + F2 + F3 + F4 FΣ - равнодействующая сила. Фигура ОАВСD – называется силовым многоугольником, замыкающая сторона которого представляет равнодействующую этих сил. При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится. Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим. ЗАМЕЧАНИЕ. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю. Следовательно, при геометрическом построении конец последнего вектора должен совпадать с началом первого. Если плоская система сходящихся находится в равновесии, многоугольник сил этой системы должен быть замкнут.
A F2 F1 B O F5 F3 F4 C
D
FΣ = 0, силовой многоугольник замкнут., система сил находится в равновесии.
2. Аналитический способ определения равнодействующей.
В системе сходящихся сил равнодействующая может быть найдена через проекции составляющих. y
Fy F α
Fx = Fcosα x Fy = Fcos(90o- α) 0 Fx
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Ввиду того, что проекции между собой образуют прямой угол, можно записать: F =
Пример: y
x 60 30 F Fx = - Fcos600 Fy = - Fcos30o F =
Условия равновесия плоской системы сходящихся сил В аналитической форме.
Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Равнодействующая в этом случае равна нулю. (FΣ = 0), тогда проекции этих сил
FΣx = FΣy = Значение равнодействующей определяется по формуле: FΣ =
Оба слагаемых положительных,т.к возведены в квадрат. Поэтому FΣ = 0 возможнотолько тогда,когда:
Условие равновесия в аналитической форме в аналитической форме можно сформулировать следующим образом:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.10 (0.007 с.) |

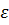
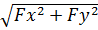
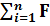 ix
ix