
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи теоретической механики.Содержание книги
Поиск на нашем сайте
Министерства обороны Российской Федерации
КОНСПЕКТ ЛЕКЦИЙ по разделу 1 «Теоретическая механика» дисциплины ОП.02. Механика. для специальностей: 26.02.03 Судовождение 26.02.05 Эксплуатация судовых энергетических установок. 26.02.06 Эксплуатация судового электрооборудования и средств автоматики
Составлен преподавателем Дымдымарченко С.А
Г.Ломоносов 2020г.
Содержание 1. Ведение………………………………………………………………………3 2. Задачи теоретической механики……………………………………………8 3. Тема 1.1.Основные понятия и аксиомы статики…………………………..9 4. Тема 1.2.Плоская система сходящихся сил……………………………….15 5. Тема 1.3.Пара сил и момент силы относительно точки………………….19 6. Тема 1.4.Плоская система произвольно расположенных сил……………21 7. Тема 1.5.Центр тяжести тела……………………………………………….25 8. Тема 1.6. Кинематика……………………………………………………….28 9. Тема 1.7. Простейшие движения твердого тела…………………………..35 10. Тема 1.8. Динамика. Основные понятия и аксиомы динамики………...39 11. Тема 1.9. Движение материальной точки. Метод кинетостатики………43 12. Тема.1.10. Работа и мощность……………………………………………49 13. Литература…………………………………………………………………55
Введение. Механика - комплексная дисциплина. Она включает три раздела: «Теоретическая механика», «Сопротивление материалов», «Детали машин». «Теоретическая механика» - раздел, в котором излагаются основные законы движения твёрдых тел и их взаимодействия. В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчётов элементов конструкций на прочность, жёсткость и устойчивость под действием внешних сил. В заключительном разделе «Детали машин» рассматриваются основы конструирования и расчёта деталей и сборочных единиц общего назначения
Дисциплина «Механика» является общепрофессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем.
Краткий исторический очерк. Термин «механика» был введен великим философом древности Аристотелем (384-322 гг. до н. э.). Происходит он от греческого слова «механе», что означает «ухищрение», «машина». Вообще механика наряду с математикой и астрономией является одной из самых древних наук. Египетские пирамиды, сооруженные более трех тысяч лет до новой эры, остатки еще более древних сооружений Индии и Китая свидетельствуют о том, что в глубокой древности применялись катки, рычаги, блоки, облегчающие поднятие тяжестей. Однако моментом возникновения механики - науки следует считать появление первых сочинений, теоретически обобщивших накопленный опыт. Поэтому основоположником механики следует считать величайшего ученого Древней Греции Архимеда (287-212 гг. до н. э.). Архимед дал решение задачи о рычаге, открыл закон о давлении жидкости на погруженное в нее тело, носящий его имя, дал определение центра тяжести. Им были разработаны методы определения площадей и объемов. Метательные машины, изобретенные Архимедом, позволяют предполагать, что он имел четкие понятия о динамике материальных тел. Научные труды Аристотеля содержат законченный взгляд на мир и представляли собой энциклопедию античной мысли. Именно этим, несмотря на ошибочность многих его взглядов, по - видимому, объясняется столь сильное воздействие его трудов на научную мысль Европы вплоть до эпохи Возрождения. Приведем лишь некоторые взгляды Аристотеля, из-за которых было бы ошибочно считать его основателем механики как науки. Например, он писал: «Падение куска золота или свинца или любого другого тела, наделенного весом, происходит тем быстрее, чем больше его вес...». Аристотель приводит такие примеры: лошадь непрерывно напрягается, чтобы тянуть повозку, камень опускается на дно озера. Поэтому он делает вывод, что тяжелые предметы падают быстрее, чем легкие. Чтобы повозка двигалась, необходимо прикладывать усилия.
То есть Аристотель никогда не рассматривал то, что мы называем силами трения или сопротивления, как силы, отдельные от движения. Это отделение было осуществлено Галилео Галилеем (1564-1642), благодаря которому возникло понятие инерции и начали складываться современные взгляды на движение тел. Интенсивное развитие механики относится к XV-XVII столетиям, когда общественная практика (торговое мореплавание, военное дело и промышленность) поставила перед учеными ряд проблем, связанных с движением небесных тел, полетом артиллерийских снарядов, прочностью корабля, машин и строительных сооружений. Усовершенствование техники, определение географических координат с помощью астрономических наблюдений потребовало пересмотра теории движения небесных тел и привело к открытию гелиоцентрической системы мира И. Коперником (1473-1543). Система Коперника была чисто кинематической. Законы динамики присутствовали в ней в скрытом виде. До Коперника общепризнанной была геоцентрическая система мира Птолемея (II в.), несмотря на то, что еще древние греки располагали фактами в пользу гелиоцентрической системы мира. Однако греческие астрономы отвергали гелиоцентрическую систему, так как для большинства греческих философов, в том числе и Аристотеля, Земля - обитель человечества - была наиболее важным объектом во Вселенной и было немыслимо, чтобы этот центр Вселенной имел какое-то движение. Следующим шагом было открытие Иоганном Кеплером (1571—1630) законов движения планет. Он установил, что орбиты планет представляют собой не окружности, а эллипсы с небольшим эксцентриситетом. Законы, открытые Кеплером, позволили Ньютону обосновать закон всемирного тяготения. Галилей впервые исследовал динамическое действие сил на движущееся тело и поэтому по праву является основоположником динамики. Галилеем были проделаны наиболее точные для своего времени опыты по изучению свободного падения тел. В результате этих экспериментов он установил пропорциональность пройденного пути при падении квадрату времени, что означало независимость ускорения в пустоте от веса тела. Галилей доказал, что траекторией движения тела, брошенного в пустоте под углом к горизонту, является парабола. Галилей заложил также основы современной кинематики. Однако наиболее важным открытием Галилея является открытие закона инерции, после чего началось формирование современных взглядов на механическое движение.
Среди выдающихся ученых XVII в. следует отметить французского философа Рене Декарта (1596-1650), который сформулировал идею сохранения механического движения. Замечательный исследователь Христиан Гюйгенс (1629-1695) обобщил понятие ускорения, введенного Галилеем, на случай криволинейного движения и впервые осуществил разложение ускорения на касательную и нормальную составляющие. Гюйгенс создал теорию математического и физического маятников. Гюйгенс использовал понятие об осевых моментах инерции, а также кинетической энергии, но не пользовался этими терминами. Исаак Ньютон (1643-1727) в своем труде «Математические начала натуральной философии» (1687) подвел итог достижениям своих предшественников и сформулировал три основных закона механики, наметил пути дальнейшего развития механики. Ньютон ввел понятие массы и впервые обратил внимание на эквивалентность инертной и тяготеющих масс, проводя опыты над качающимися маятниками, выполненными из различных материалов.
Блестящие результаты дало применение закона всемирного тяготения, открытого Ньютоном, к решению астрономических задач. Так, например, и были открыты Нептун в XIX в. и Плутон в XX в., которые ранее в телескоп не наблюдались ввиду малой светимости, и были обнаружены лишь тогда, когда было предсказано их местоположение на небесной сфере. Одним из выдающихся современников Ньютона был немецкий философ и математик Готфрид Лейбниц (1646-1716). Лейбниц одновременно с Ньютоном открыл исчисление бесконечно малых. В области механики Лейбницу принадлежит установление понятия о «живой силе». В связи с этим возникла дискуссия между сторонниками Лейбница и Декарта о мерах движения. Декарт под мерой движения понимал «количество движения», равное по величине произведению массы точки на ее скорость. Лейбниц противопоставлял ей «живую силу», пропорциональную массе и квадрату скорости движения. Эта дискуссия была прекращена Даламбером, показавшим непротиворечивость обоих мер движения. Леонарду Эйлеру (1707-1783) принадлежат выдающиеся заслуги в развитии механики в посленьютоновский период, Л. Эйлер был членом Российской Академии наук с 1727 г. Эйлер является основоположником динамики твердого тела и гидромеханики, ему принадлежит общепризнанный метод кинематического описания движения твердого тела, имеющего неподвижную точку, с помощью трех углов, носящих его имя. Эйлером также была получена формула для скоростей точек тела, вращающегося вокруг неподвижной точки. Им была сформулирована и доказана теорема об изменении момента количества движения. Он заложил основы теории корабля, турбин, теорию устойчивости упругих стержней. Современник Эйлера Михаил Васильевич Ломоносов (1711-1765) открыл закон сохранения вещества. Он создал кинетическую теорию газов и распространения тепла. Им был сформулирован закон сохранения количества движения. Значительный вклад в динамику несвободных систем был сделан выдающимся французским ученым Жаном Лероном Даламбером (1717-1783), которому принадлежит формулировка принципа механики, носящего его имя. Однако Даламбер не располагал общими аналитическими методами решения задач динамики несвободных систем. Общие аналитические решения задач динамики несвободных систем были разработаны Ж.-Л. Лагранжем (1736-1813) в его основополагающей работе «Аналитическая механика» (1788). За основу был взят принцип Лагранжа - Даламбера, являющийся синтезом принципа виртуальных перемещений Лагранжа и принципа Даламбера.
Механика XIX века связана с именами Михаила Васильевича Остроградского (1801-1861), Уильяма Гамильтона (1805-1865), Карла Якоби (1804-1851), Карла Фридриха Гаусса (1777-1855). В частности, важное значение в механике имеет вариационный принцип Гамильтона - Остроградского. Для построения общей теории интегрирования дифференциальных уравнений динамики предпочтительнее иметь дело с уравнениями первого порядка с их так называемой «канонической формой». В 1842 г. Якоби в «Лекциях по динамике» изложил метод интегрирования канонических уравнений. Основополагающий вклад в кинематику механизмов был проделан вы дающимся математиком и механиком Пафнутием Львовичем Чебышевым (1821-1894). Его ученик Александр Михайлович Ляпунов (1857-1918) получил всемирную известность благодаря трудам по устойчивости и движения. Ляпунову принадлежит строгая постановка задачи об устойчивости движения и наиболее общих методов ее решения. Выдающуюся роль в механике сыграл Николай Егорович Жуковский (1847-1921). Он является основоположником современной гидродинамики и аэродинамики. Жуковский теоретически обосновал возможность сложных движений самолета. Ряд исследований Жуковского относится к вопросам теории устойчивости движений, динамике твердого тела, вопросам аэродинамического расчета самолетов. Ученик Жуковского Сергей Александрович Чаплыгин (1869-1942) стал основоположником газовой динамики больших скоростей. Его работы по теории крыла и газовой динамике значительно опередили время, получив широкое применение лишь в 50-х годах XX столетия. Большой вклад в механику внес кораблестроитель Алексей Николаевич Крылов (1863-1945), известный своими трудами в области теории качки корабля, прочности его корпуса, теории плавучести и непотопляемости. Задачи динамики твердого тела всегда играли значительную роль в механике. Здесь следует упомянуть Софью Васильевну Ковалевскую (1850 1891). Ее работа является наиболее значительной в цепи преемственности трудов, начиная с Эйлера и Лагранжа. Более того, оказалось, как это было доказано Ляпуновым, что случаи Эйлера, Лагранжа и Ковалевской являются единственными, в которых уравнения вращений твердого тела допускают однозначные интегралы при всех значениях аргумента и начальных условиях. Наиболее крупные результаты по теории устойчивости после А. М. Ляпунова получены Н. Г. Четаевым (1902-1959). Теория колебаний, линейных и нелинейных, получили существенное развитие в трудах А. Н. Крылова (1863-1945), Н. М. Крылова (1879-1955), Н. Н. Боголюбова (1909-1992), Л. Н. Мандельштама (1879-1944), А. А. Андронова (1901-1952), Б. В. Булгакова (1900-1952), Ю. А. Митропольского (1917-2008). Значительный вклад в теорию устойчивости движения и ряд достижений в области линейной и нелинейной теории упругости принадлежит А. И. Лурье (1901-1979). Л. Г. Лойцанский (1900-1995) внес значительный вклад в гидроаэродинамику.
Основоположником механики тел переменной массы является И. В. Мещерский (1859-1935). К. Э. Циолковский (1857-1935) создал основы теории реактивного движения и реактивной техники. В XX веке появилась релятивистская механика А. Эйнштейна (1879 1955). В настоящее время интенсивное развитие получила механика космического полета.
Тема 1.1. Основные понятия и аксиомы статики. В отличие от физики теоретическая механика изучает законы движения некоторых абстрактных абсолютно твёрдых тел: здесь материалы, форма тел существенного значения не имеет. При движении абсолютно твёрдое тело не деформируется и не разрушается. В случае когда размерами тела можно пренебреч, тело заменяют материальной точкой. Это упрощение принятое в механике облегчает решение задач. Материальна точка – тело размерами которого можно пренебречь. Абсолютно твёрдое тело – это тело, расстояние между двумя точками которого, остается неизменным. Одним из основных понятий механики является понятие о силе. Сила – векторная величина, количественная мера механического взаимодействия между телами. Это значит, что сила характеризуется тремя факторами: 1) численным значением 2) направлением 3) точкой приложения В качестве примеров сил можно назвать силу притяжения к Земле, всевозможные контактные силы, например, давление на опоры сооружения, силы, возникающие из-за сопротивления среды.
F2 F F1 a
v
Силы, действующие на тело делятся на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил. Внутренние силы возникают в теле под действием внешних сил.
Модуль или численное значение силы в системе СИ измеряется в Ньютонах (Н). 1 КН = 103 Н 1 МН = 106 Н 1 кГс = 9,81Н 1 Н = 0,1 кГс
Линия действия силы – прямая проведённая по направлению силы, неограниченно в обе стороны. Система сил – совокупность нескольких сил, приложенных к телу. Аксиомы статики. 1. Первая аксиома - закон инерции. Система сил, приложенная к материальной точке, является уравновешенной, если под её воздействием точка находится в состоянии относительного покоя или движется равномерно и прямолинейно.
2. Вторая аксиома устанавливает условие равновесия двух сил. Две равные по модулю или численному значению силы (F1 = F2) приложенные к абсолютно твёрдому телу и направленные по одной прямой в противоположные стороны взаимно уравновешиваются.
3. Третья аксиома служит основой для преобразования сил. (Принцип присоединения или исключения уравновешенных сил) Не нарушая механического состояния абсолютно твёрдого тела, к нему можно приложить или отбросить от него уравновешенную систему. Уравновешенная система сил эквивалентна нулю. Следствие из второй и третьей аксиом: Всякую силу, действующую на тело можно перенести вдоль линии её действия в любую точку тела не нарушая при этом равновесия.
4. Четвёртая аксиома определяет правило сложения сил. (Правило параллелограмма) Равнодействующая двух сил, приложенных водной точке, приложена в этой точке и является диагональю параллелограмма, построенного на данных силах. F1 FΣ F2
5. Пятая аксиома устанавливает. Что в природе не может быть одностороннего действия. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.
Связи и реакции связей.
Все законы и теоремы статики справедливы для свободного твёрдого тела. Все тела делятся на свободные и несвободные (связанные). Свободным называют тело, которое не испытывает никаких препятствий для перемещения в пространстве любом направлении. Если тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным (связанным). Связь - тело, которое ограничивает движение рассматриваемого тела. При взаимодействии между телом и связью возникают силы. Эти силы действуют со стороны связей и называются реакциями связей. Реакция связи (R) – сила возникающая в связи под действием данного тела. Реакция связи всегда противоположна тому направлению, по которому связь препятствует телу двигаться. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей). Все связи можно разделить на несколько типов.
Виды связей в механике. 1. Связь в виде гладкой (т.е. без трения) плоскости или поверхности. F
R R
Реакция перпендикулярна к опорной плоскости.
2. Связь в виде контакта с цилиндрической или шаровой поверхности.
R
Реакция перпендикулярна к опорной плоскости.
3. Связь в виде шероховатой плоскости.
F
Rt Rn R ρ
Здесь возникают две составляющие реакции: нормальная Rn и касательная Rt, лежащая в плоскости. Rt называется силой трения и всегда направлена противоположно возможному движению. Т.е R = Fтр + Rn Реакция R отклоняется от нормали на некоторый угол ρ. Однако силы трения незначительны и ими часто пренебрегают. 4. Гибкая связь (трос, цепь, канат).
RA RB A B
G
Реакции гибких связей RA и RB направлены вдоль связей, причём гибкая связь может работать только на растяжение.
5. Связь в виде жёсткого прямого стержня с шарнирным закреплением концов.
R3
R1 R2 G
R1 , R2 и R3 всегда направлены вдоль осей стержня. Стержни при этом могут быть как растянутыми так и сжатыми. 6. Связь, осуществляемая ребром двугранного угла или точечной опорой.
R1 R2 G
Реакция такой связи направлена перпендикулярна поверхности тела.
Пример решения задачи: Груз F = 20кг подвешен на тросе АВ. Определить реакцию троса.
Решение В ° Рассмотрим равновесие груза. Действие связи (троса) на тело заменяем его реакцией. Так как нить препятствует перемещению груза вниз, то реакция FA направлена в противоположную сторону – вверх. А FA Груз находится в равновесии под ° действием двух сил, направленных по одной прямой в противоположные стороны, F F следовательно (на основании второй аксиомы статики), эти силы равны по модулю, т.е. FA = F = 20кг
В аналитической форме.
Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Равнодействующая в этом случае равна нулю. (FΣ = 0), тогда проекции этих сил
FΣx = FΣy = Значение равнодействующей определяется по формуле: FΣ =
Оба слагаемых положительных,т.к возведены в квадрат. Поэтому FΣ = 0 возможнотолько тогда,когда:
Условие равновесия в аналитической форме в аналитической форме можно сформулировать следующим образом: Правило знаков
l l
+ _
Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки и отрицательным, если пара стремится вращать тело против часовой стрелки Это правило условно.
2.Сложение и равновесие пар сил на плоскости. Подобно силам пары сил можно складывать. Пара заменяющая собой действие данных пар называется результирующей.
М1 М2
М3
М3
МΣ = М1 + М2 + М3 или МΣ = М1 + М2 - М3
Т.е.момент результирующий пары равен сумме моментов составляющих пар.
Условие равновесия Правило знаков + F F -
O a a O
Момент положительный, если сила стремится вращать тело по часовой стрелке. Момент отрицательный, если сила стремится вращать тело против часовой стрелке. Точка О относительно которой берется момент называется центром момента, а длина перпендикуляра а называется плечом силы относительно центра момента. М0(F) = F a [ Нм ]
2. Приведение плоской системы сил к данной точке. Рассмотрим случай переноса силы в произвольную точку, не лежащую на линии действия силы.
Возьмем силу F, приложенную в точке С. Требуется перенести эту силу параллельно F самой себе в некоторую точку О. Приложим l F´ в точке О две силы F´и F´´ противоположно- направленные, равные по значению и 900 параллельные заданной силе F, т.е F´ = F´´ = F F´´ От приложения в т. О этих сил состояние тела не изменяется, так как они взаимно уравновешиваются. Эту систему можно рассматривать как состоящую из силы F´ приложенной в точке О и пары сил F и F´´ моментом M = Fl. Эту пару си называют присоединенной. Таким образом, при приведении силы F к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, такой же по модулю и направлению, как и сила F, и присоединенной пары сил, момент которой равен моменту данной силы относительно точки приведения. М0(F) = F • l Главный вектор – векторная сумма всех сил, приведенная к данной точке. Обозначается - FΣ Главный момент – алгебраическая сумма моментов всех пар сил, относительно точки приведения. Обозначается - МΣ При равновесии главный вектор системы равен нулю и главный момент должен равняться нулю. Этот метод приведения одной силы можно применить к какому угодно количеству сил.
Виды опор балок 1. Шарнирно- подвижная опора (допускает поворот вокруг оси и линейное перемещение). На схемах: Ray
A
2. Шарнирно-неподвижная опора (допускает прворачивание вокруг оси шарнира). На схемах: Ray
Rax A
3. Жесткая заделка (балка с защемленным концом). На схемах: Rx
Ry
Mоп Виды нагрузок
1. Сосредоточенная нагрузка.
Р Fy F Fx = Fcos α Fx Fy = Fcos (90- α) 2.Распределенная нагрузка.
q
l
Q = q• l
План расчета балочной системы 1. Составляют схему балки со всеми размерами и нагрузками (обычно задается). 2. Составляется расчетная схема балки: а) опоры балок заменяются на их реакции б) распределенная нагрузка заменяется сосредоточенной в) силы,расположенные под углом от оси балки, заменяются на вертикальные и горизонтальные проекции г) составляют три условия равновесия Σ Fx = 0 Σ Fx = 0 ΣМА= 0 Σ Fy = 0 или ΣМА= 0 или ΣМВ= 0 ΣМА= 0 ΣМВ= 0 ΣМС= 0 3. Делается проверка. Для этого составляется уравнение из другой группы уравнений.
Центр тяжести тела
1. Центр параллельных сил и его свойства.
Установим одно важное свойство точки приложения равнодействующей силы двух параллельных сил. Пусть в точках А и В на тело действуют параллельные силы F1 и F2 А С В
α α α F2 F2´ F1´ F1
FΣ´ FΣ
Равнодействующая этих сил равна их сумме, параллельна им, направлена в ту же сторону, а ее линия действия делит прямую АВ на части обратно пропорциональные этим силам.
Далее повернем силы на некоторый угол т.е изменим направление сохранив параллельность. При этом равнодействующая останется равной их сумме, параллельной им, направленной в ту же сторону, а линия ее действия опять поделит прямую АВ на части, обратно пропорциональные величинам заданных сил. Точкой С обозначено пересечение линии действия равнодействующей с линией АВ. Эта точка называется центром параллельных сил, а ее положение не зависит от направления слагаемых сил. Любое тело можно рассматривать как состояние из большого числа малых частиц, на которые действуют силы тяжести. Эти силы направлены к центру Земли по радиусу. Так как размеры тел, с которыми приходится иметь дело в технике, ничтожно малы по сравнению с радиусом Земли( Равнодействующая этих сил называется силой тяжести. Центр параллельных сил тяжести, действующих на все частицы тела, называется центром тяжести тела. Центр тяжести тела не меняет своего положения при повороте тела.
2. Координаты центра тяжести.
Xc =
i – количество фигур ( ,, ) Si – площади элементарных фигур xi и yi координаты центра тяжести элементарных фигур Т.е. любую фигуру можно разбить на элементарные
3. Центр тяжести элементарной плоской фигуры.
Центр тяжести прямоугольника и квадрата находится на пересечении диагоналей. yi S = a xi
Центр тяжести круга находится в центре круга.
yc S = π r 2
xc
Центр тяжести треугольника лежит на пересечении медиан на расстоянии треугольника. S =
Пример определения центра тяжести сложной фигуры: y 1 2 С2 с3 9
40 С1
x 10 24 6
1. Устанавливаем систему координат. 2. Разбиваем на элементарные фигуры. 3. Определяем площади и координаты центров тяжести элементарных фигур.
В нашем случае два прямоугольника и треугольник:
S1 = 40 S2= 24 S3 = 4. По формулам определяем координаты центра тяжести сложной фигуры. Xс =
Yc =
Центр тяжести тела
Xc = | |||||||||
|
| Поделиться: |

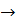
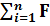 ix
ix
 =
= 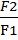
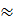 637 км), то можно считать, что приложенные к частицам силы тяжести параллельны и вертикальны. Следовательно, силы тяжести отдельных частиц тела образуют систему параллельных сил
637 км), то можно считать, что приложенные к частицам силы тяжести параллельны и вертикальны. Следовательно, силы тяжести отдельных частиц тела образуют систему параллельных сил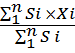 Yc =
Yc = 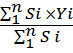
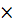 b
b высоты от основания
высоты от основания a
a 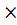 b
b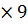 = 216 мм2 x2 = 22 мм y2 = 35, 5 мм
= 216 мм2 x2 = 22 мм y2 = 35, 5 мм 6
6  =
= 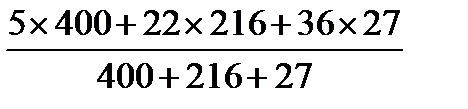 =
=  =12 мм
=12 мм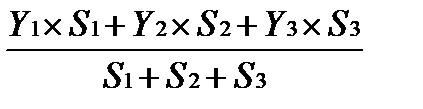 =
= 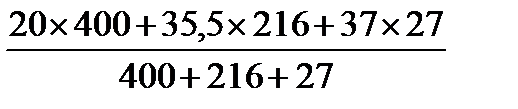 =
= 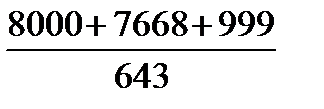 =26 мм
=26 мм


