Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ознакомьтесь с условием задачи и разберите ее решение.Содержание книги
Поиск на нашем сайте
В правильной четырехугольной пирамиде высота равна 4 см., а боковое ребро – 5 см. Найдите угол, образованный боковым ребром с плоскостью основания.
Решение: 1. SD- - наклонная к α, SO⟘α, значит ОD – проекция SD на плоскость α (ОD= прαSD). 2. ∠(SD,α)=∠SDО (по определению). 3. SO⟘α, ОD 4.
ΔSOD – прямоугольный (по п.3).4
Ответ:
Проанализируйте решение задачи и допишите в приведенном решении нужные обоснования.
Боковое ребро правильной шестиугольной пирамиды равно 5 см, а сторона основания – 6 см. найдите площадь ее боковой и полной поверхности Решение:
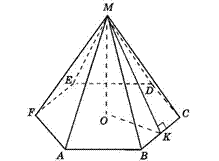 Площадь боковой поверхности правильной пирамиды равна произведению основания на , Площадь боковой поверхности правильной пирамиды равна произведению основания на ,
т. е. Sбок = * d, где d = MK = √,
= (см).
= (см), Sбок = * = (см2).
2) S
пол
= + S
осн
, где S
осн
=
= √ (см2). Следовательно, Sпол = + (см2). Ответ: Sбок = , Sпол = + (см2).
4. Ознакомьтесь с условием задачи и запишите ее решение по указанному плану. 5. В правильной четырехугольной пирамиде боковое ребро, равное 10 дм., образует с плоскостью основания угол равный 600. Найдите высоту пирамиды.
Решите задачи. 1.
 Апофема пирамиды равна 5см., а высота 4см. Найдите площадь полной поверхности пирамиды Апофема пирамиды равна 5см., а высота 4см. Найдите площадь полной поверхности пирамиды
Ответ:
2.
5. Выполните задания. 1. Составьте задачу на нахождение объема прямой пирамиды. Решите еѐ. Задача:
2. Составьте задачу на нахождение объема правильной пирамиды. Решите еѐ. Задача:
2.4. Задачи для самостоятельного решения. 1. Дана правильная четырехугольная пирамида со стороной основания 4см. высота пирамиды равна 5 см. Найдите боковое ребро пирамиды и ее объем. 2. В основании пирамиды лежит прямоугольник со сторонами 3см. и 4см. Высота пирамиды равна 8 см. Найдите площадь полной поверхности пирамиды. 3. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 12см., а боковая сторона - 10см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Найдите высоту пирамиды. 4. Высота и апофема правильной четырехугольной пирамиды соответственно равны 4 и 17 см. Вычислите объем пирамиды. 5. Основание пирамиды – квадрат. Сторона основания равна 20 дм, а еѐ высота равна 21 дм. Найдите объѐм пирамиды.
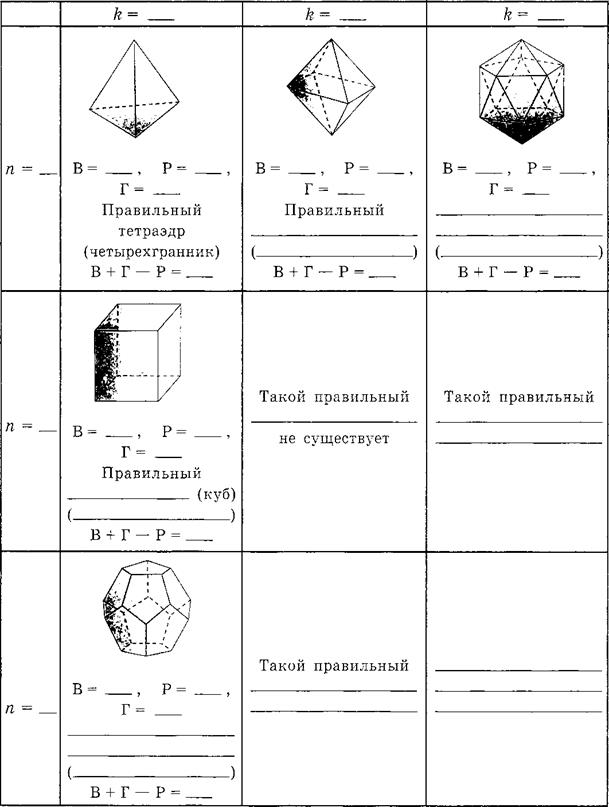
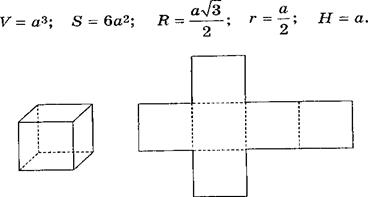
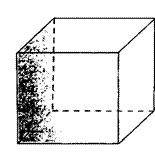
Правильные многогранники 3.1 Теоретические сведения Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер. Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны. Существует пять различных правильных многогранников (выпуклых): куб, правильный тетраэдр, правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (додекаэдр), правильный двадцатигранник (икосаэдр). В приведенных ниже формулах использованы следующие обозначения: V — объем многогранника, S — площадь поверхности, R — радиус описанной сферы, r — радиус вписанной сферы, Н — высота многогранника, а — каждое из равных ребер многогранника. а) Куб Все шесть граней куба — равные квадраты (рис. 5).
Рис. 5
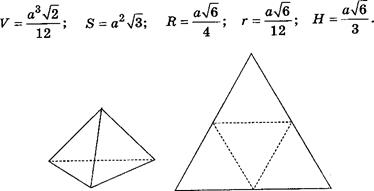
б) Правильный тетраэдр Все четыре грани — равные правильные треугольники (рис. 6).
Рис. 6 в) Правильный октаэдр Все восемь граней — равные правильные треугольники (рис. 7).
Рис.7 г) Правильный додекаэдр
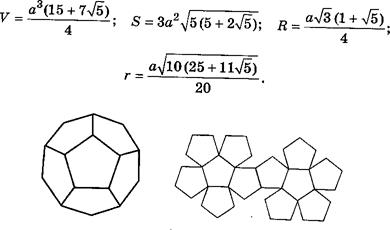
Все двенадцать граней — равные правильные пятиугольники (рис.8). Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Сумма плоских углов при каждой вершине додекаэдра равна 324°. Рис. 8 д) Правильный икосаэдр Все двадцать граней — равные правильные треугольники (рис. 9). Каждая вершина икосаэдра является вершиной пяти треугольников. Сумма плоских углов при каждой вершине икосаэдра равна 300°.
Рис. 9 3.2 Упражнения 1. Заполните пропуски
1.Выпуклый называется правильным, если его грани - многоугольники, и в его сходится одно и то же число. 2.Существует правильных многогранников. 3. Тетраэдром называется .
4.Кубом называется . 5.Октаэдром называется . Икосаэдром называется . 6. Додекаэдром называется . 2.Докажите, что куб является правильным многогранником. Доказательство: Проверим, обладает ли куб всеми признаками правильного , указанными в определении. 1) Куб выпуклым многогранником. 2) Каждая грань куба - , т. е. многоугольник, и все грани между собой 3) Итак, у куба все признаки, указанные в определении многогранника. Следовательно, куб правильным , что и требовалось доказать.
Вычислите для каждого из них величину В + Г – Р.
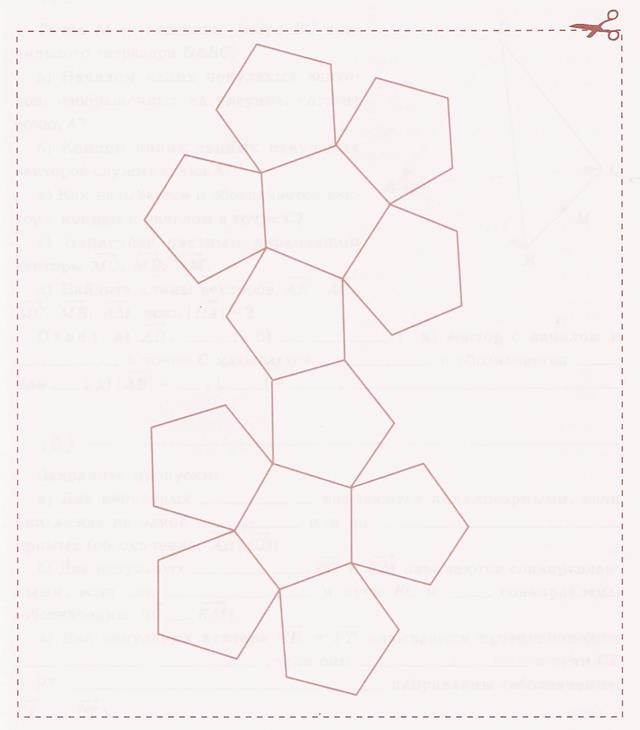
3. а) Дорисуйте на развертке правильного додекаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника. б) Измерьте длину ребра и вычислите площадь поверхности правильного додекаэдра.
Ответ. б) см2.
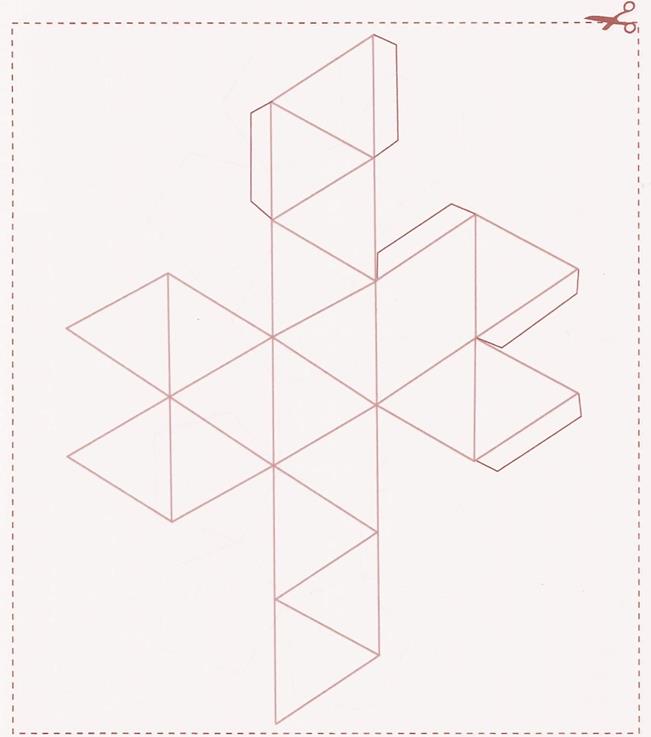
4.а) Дорисуйте на развертке правильного икосаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника. б) Измерьте длину ребра и вычислите площадь поверхности правильного икосаэдра. Ответ. б) см2. -
5. а) Дорисуйте на развертке правильного додекаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника. б) Измерьте длину ребра и вычислите площадь поверхности правильного додекаэдра. Ответ. б) см2.
Список литературы 1. Алешина Т. Н. Обучающие и проверочные задания. Геометрия. 10 класс (Тетрадь)/ Алешина Т. Н. – М: Интелект – Центр. – 2011. – 108 с. 2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., «Геометрия: учебник для 10-11 кл.» - М: Просвещение, 2009.-256 с.
3. Глазков Ю. А., Юдина И.И. Геометрия 10 класс. Рабочая тетрадь: учебное пособие для общеобразоват. учреждений (базовый и профильный уровни) / М.: Просфещение, 2011. – 95 с. 4. Евдокимов Н. ИН. Краткий справочник по математике. 9 – 11 классы. – СПб.: Издательский Дом «литера», 2010. – 288 с. 5. Смирнова И.М. Геометрия 10 класс. Рабочая тетрадь: учебное пособие для общеобразоват. учреждений/ И. М. Смирнова, В. А. Смирнов. – М.: Мнемозина, 2009. – 103 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.48.105 (0.009 с.) |


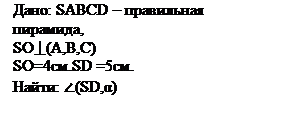
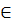 α, следовательно, SO⟘ОD (по определению прямой, перпендикулярной плоскости).
α, следовательно, SO⟘ОD (по определению прямой, перпендикулярной плоскости).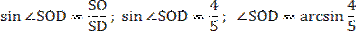
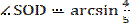


 CK =
CK = 


 Итак, d = √ = √ = (см), Р = 6 * =
Итак, d = √ = √ = (см), Р = 6 * =
 = √
= √


 Решение
Решение  Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна a. Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30°. Найдите площадь боковой поверхности пирамиды.
Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна a. Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30°. Найдите площадь боковой поверхности пирамиды.


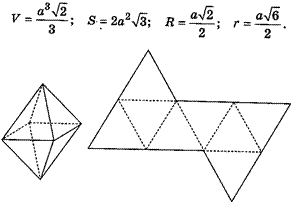
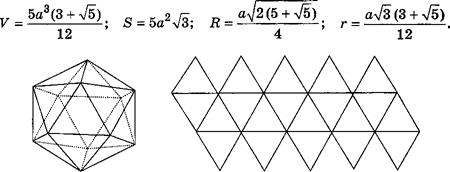
 В вершине куба сходится число ребер, а именно ребра.
В вершине куба сходится число ребер, а именно ребра.