Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пирамида. Усеченная пирамида.Содержание книги
Поиск на нашем сайте
2.1 Теоретические сведения
Рис. 3 Отрезки Высота пирамиды – перпендикуляр SP, проведенный из вершины пирамиды к плоскости основания. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), пятиугольной (n=5) (рис. 4) и так далее. Альтернативное название треугольной пирамиды – тетраэдр.
Рис. 4 Площадь полной поверхности пирамиды равна сумме площадей всех ее граней: S полн. = S осн.+ S бок., где S осн – площадь основания, S бок – площадь боковой поверхности пирамиды.
Площадь боковой поверхности правильной пирамиды вычисляется по формуле: S бок. = ½ ∙ P осн ∙ d, где Р – периметр основания пирамиды, d – апофема (высота боковой грани, проведенная из вершины). Объем пирамиды вычисляется по формуле:
где Sосн – площадь основания пирамиды, h – высота пирамиды.
Перпендикуляр, проведенный из какой – либо точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке СН – высота усеченной пирамиды. Боковые грани усеченной пирамиды представляют собой трапеции. Усечѐнная пирамида, полученная из правильной пирамиды, сечением, параллельным еѐ основанию, называется правильной усечѐнной пирамидой.
Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называется апофемами. Площадь боковой поверхности усеченной пирамиды равна сумме площадей ее боковых граней. Площадь боковой поверхности правильной усечѐнной пирамиды равна произведению полусуммы периметров оснований на апофему.
где Р, р – периметры оснований пирамиды, h – апофема. Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и площади боковой поверхности пирамиды. Объем усеченной пирамиды вычисляется по формуле:
3 1
где h – высота усеченной пирамиды, S и S1 - площади оснований усеченной пирамиды. Упражнения 1. Выполните чертеж четырехугольной пирамиды, обозначьте ее и запишите:
основание
Закончите предложения. 1. Высотой пирамиды называется
2. Пирамида называется правильной, если
3. Апофемой правильной пирамиды называется
4. Площадью полной поверхности пирамиды называется
5. Площадью боковой поверхности пирамиды называется
6. Усеченная пирамида – нижний многогранник, отсекаемый от пирамиды плоскостью, параллельной
7. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью
8. Выпуклый многогранник называется правильным, если
9. Примеры моделей пирамиды и правильных многогранников из вашей профессии: _
3. Ответьте на вопросы: 1. Сколько сторон основания, боковых ребер, вершин имеет семиугольная пирамида?
2. Сколько оснований у усеченной пирамиды?
3. Какие многоугольники лежат в основаниях правильной усеченной шестиугольной пирамиды?
4. Сколько боковых граней у шестиугольной пирамиды?
5. Как называется точка пресечения всех боковых ребер пирамиды?
6. В каком взаимном расположении находятся ребро основания и апофема пирамиды?
7. Какая фигура может лежать в основании прямой четырехугольной пирамиды?
8. Из каких фигур состоит пирамида?
9. Сколько боковых ребер и сторон основания у десятиугольной пирамиды?
10. Сколько боковых ребер и сторон основания у семиугольной усеченной пирамиды?
11. Сколько (и какие) виды правильных выпуклых многогранников Вы знаете?
12. Какое наименьшее число ребер, граней, вершин имеет правильный многогранник? Как он называется? 13. Всякий ли параллелограмм может быть основанием правильной пирамиды? Ответ поясните
14. Может ли правильный многоугольник быть основанием неправильной пирамиды? Ответ поясните
15. Основанием треугольной пирамиды является равносторонний треугольник. Одна
4. Выполните задания. 1. Среди изображенных тел выберите номера тех, которые являются пирамидами.
1 2 3 4 5 6 7
Ответ:
2.
SABCD – правильная четырехугольная пирамида. Проведите высоту SO. Как определить угол между боковым ребром пирамиды и плоскостью основания? Чему равен этот угол, если предположить, что высота SO вдвое меньше бокового ребра?
3.
правильной четырехугольной усеченной
6. Поясните, что является осью симметрии: а) квадрата б) окружности в) правильного треугольника г) параллелограмма д) ромба
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 738; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.188.105 (0.008 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

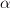
 Рассмотрим плоскость, многоугольник
Рассмотрим плоскость, многоугольник 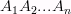 , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой.
, лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой.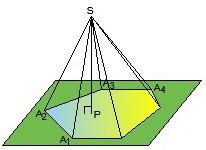
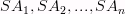 называются боковыми ребрами. Многоугольник A 1 A 2… An называется основанием, а треугольники с общей вершиной – боковые грани. Точка S — вершиной пирамиды
называются боковыми ребрами. Многоугольник A 1 A 2… An называется основанием, а треугольники с общей вершиной – боковые грани. Точка S — вершиной пирамиды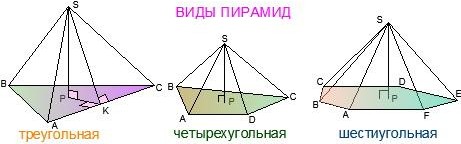

 Площадью боковой поверхности пирамиды называется сумма площадей ее боковой грани
Площадью боковой поверхности пирамиды называется сумма площадей ее боковой грани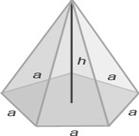


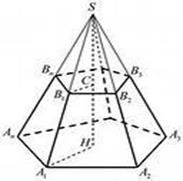

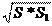 V = 1 h (S + S + ),
V = 1 h (S + S + ),

 вершины боковые ребра боковые грани
вершины боковые ребра боковые грани 


 из боковых граней ее перпендикулярна к плоскости основания. Является ли данная пирамида правильной?
из боковых граней ее перпендикулярна к плоскости основания. Является ли данная пирамида правильной?





 Сделайте рисунок пятиугольной усеченной пирамиды, обозначьте ее и запишите:
Сделайте рисунок пятиугольной усеченной пирамиды, обозначьте ее и запишите: