Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Через одиночный колебательный контурСодержание книги
Поиск на нашем сайте
1. Цель работы Изучение влияния резонансных свойств одиночного колебательного контура на глубину модуляции и форму огибающей амплитудно-модулированного колебания в случае однотональной модуляции. 2. Основные теоретические положения
Исследуемый AM сигнал представляет сумму трех гармонических составляющих:
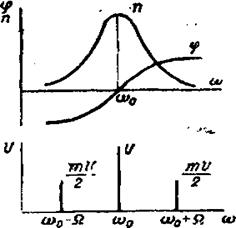
с определенными амплитудами и фазовыми соотношениями между собой. Проходя колебательный контур, составлявшие AM колебания ослабляются неодинаково (см. рис. 5.1). Уравнения нормированной резонансной кривой n- и фазового угла φ имеют вид
где I р -ток в контуре при резонансе; I ( ω ) -ток в контуре при текущей частоте; Q -добротность контура; ω р -резонансная частота контура;
При подаче на вход контура однотонально-модулированного сигнала с несущей частотой ωс, равной резонансной частоте контура (ωс=ωр), амплитуды боковых частот будут одинаково ослаблены по отношению к амплитуде несущего колебания на величину коэффициента ослабления так как для боковых частот коэффициент передачи контура в раз меньше коэффициента передачи для несущей частоты. Кроме того, боковые колебания получают дополнительные сдвиги фаз относительно несущего колебания на величину φ = arctg так как в данном случае абсолютная расстройка Δω=Ω. Мгновенное значение AM колебания на выходе настроенного контура может быть представлено в виде
где U вых= UQ —амплитуда немодулированного колебания с частотой ωc на выходе контура; Приведенные соотношения показывают, что при прохождении через настроенный контур симметрия амплитуд и фаз не нарушается, поэтому искажений формы огибающей AM колебания не происходит. Дополнительные, одинаковые по величине, но разные по знаку сдвиги фаз боковых колебаний относительно несущего колебания вызывают только сдвиг фазы огибающей выходного сигнала по отношению к входному, что не имеет особого практического значения. Однако изменение соотношения амплитуд колебаний боковых и несущей частот приводит к уменьшению глубины модуляции на величину
D = m'/m. Величина D характеризует степень изменения глубины модуляции AM колебания на выходе контура. Из приведенных выше соотношений видно, что уменьшение глубины модуляции будет тем больше, чем больше добротность Q и чем выше угловая частота Ω модуляции. При расстройке контура относительно несущей частоты колебания боковых частот получают разные изменения амплитуды и разные величины дополнительных сдвигов по фазе. Закон симметрии при этом нарушается и, кроме изменения глубины модуляции, возникают изменения формы огибающей AM колебания (становится отличной от синусоидальной). Это приводит к возникновению искажений управляющего сигнала после детектирования. При расстроенном контуре возможны как уменьшение глубины модуляции, так и ее увеличение в зависимости от степени расстройки контура и частоты управляющего сигнала.
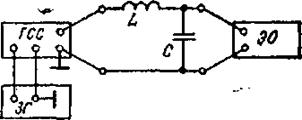
3. Описание лабораторной установки На рис. 5.1 показана схема исследования, в состав которой входят: ГСС — генератор стандартных сигналов, предназначенный для получения высокочастотных синусоидальных колебаний; ЗГ — генератор звуковых частот, предназначенный для внешней амплитудной модуляции высокочастотных колебаний ГСС; ЭО — осциллограф для наблюдения сигнала на выходе колебательного контура; L, С — элементы колебательного контура.
Рис. 5.1
4. Порядок выполнения работы 1. Ознакомиться со схемой лабораторной работы, вычертить ее, включить питание приборов и записать данные измерительных приборов. 2. Снять резонансную кривую контура Uc = Ψ(f) с помощью осциллографа, отсчитывая амплитуду Uc на экране осциллографа условно в миллиметрах. Необходимо произвести не менее 10 отсчетов (по 5 до и после резонанса). Вблизи резонанса (до и после) отсчеты проводить через 2... 3 кГц, далее — через 5 кГц.
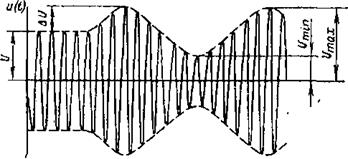
Рис. 5.2
3. Исследовать амплитудно-модулированные колебания на выходе контура при настройке его на несущую частоту (fн=fр), для чего: а) подключить зажимы «Внешняя модуляция» ГССк выходу звукового генератора ЗГ; б) с выхода ГСС подать на вход контура амплитудно-модулированное колебание с несущей частотой f н = f р и частотой управления сигнала, равной поочередно 1; 5; 10; 15 кГц; измерить (в мм) 2 Umax и 2Umin сигнала на выходе контура (рис. 5.2), поддерживая на входе коэффициент модуляции неизменным и равным 50 %.
4. Исследовать амплитудно-модулированные колебания на выходе контура при его расстройке fH ≠ fp, для этого: а) установить частоту несущего колебания fH = fp ± 5кГц и для частоты управляющего сигнала, равной 1 и 5 кГц, измерить (в мм) 2 Umax и 2Umln сигнала на выходе контура; б) зарисовать огибающие сигнала на выходе контура.
5. Содержание отчета 1. Построить резонансную кривую контура Uc = Ψ (f) и определить по ней полосу пропускания 2Δ f, добротность Q. Отметить на оси частот относительные положения несущей и боковых частот для настроенного и расстроенного контуров (рис. 5.3).
Рис. 5.3
2. Для случая f р = f н определить зависимость коэффициента модуляции AM колебания на выходе контура от частоты модуляции. Построить значения D(Ω), полученные расчетным путем, и сравнить их с экспериментальными. 3. Вычертить огибающие выходного сигнала для f н = f:р при двух значенияхчастоты (1; 15 кГц) управляющего сигнала. 4. Привести огибающие выходного сигнала, зарисованные с экрана осциллографа в случае f н ≠ f р.
Литература: [1], с. 229 – 232; [2], с. 232 - 256 Лабораторная работа 6
|
||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.85.82 (0.01 с.) |

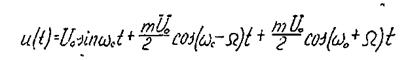
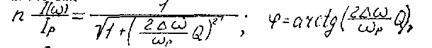
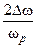 -относительная полоса пропускания контура.
-относительная полоса пропускания контура.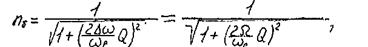
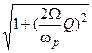
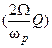 ,
,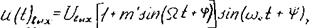
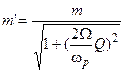 и является глубиной модуляции АМ колебания на выходе контура.
и является глубиной модуляции АМ колебания на выходе контура.