Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоретические положенияСодержание книги
Поиск на нашем сайте
Последовательный колебательный контур(рис. 4.1, а) удобно рассматривать как четырехполюсник. На резонансной частоте
а б
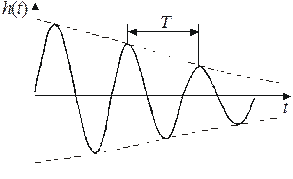
Пренебрегая сопротивлением нагрузки (полагая его достаточно большим, где в качестве входного воздействия взята взвешенная функция включения соответствует характеристическое уравнение с корнями Используя очевидные начальные условия которое при нормировке к U = 1 В становится безразмерной переходной характеристикой четырехполюсника g(t). Так как импульсная характеристика h(t) = dg/dt, получают График h(t) приведен на рис. 4.1, б. В выражении (4.3) приближение сделано в предположении малых потерь α и ωр=ω0, а также введена постоянная времени Комплексный коэффициент передачи последовательного колебательного контура в так называемом приближении малых расстроек рассчитывается просто: = Здесь принято Комплексный коэффициент передачи может быть также получен в результате применения к импульсной характеристике h (t) прямого преобразования Фурье: Нижним пределом интеграла в выражении (4.6) берут 0, так как импульсная характеристика физически реализуемого четырехполюсника существует только при t ³ 0. С использованием введенной постоянной времени АЧХ и ФЧХ цепи определяются выражениями Входное сопротивление последовательного колебательного контура на резонансной частоте мало и равно эквивалентному сопротивлению потерь,
Параллельный колебательный контур представляет собой параллельное соединение L и C элементов (рис. 4.2, а). Используют высокодобротные катушки индуктивности и конденсаторы с малыми потерями, причем потерями в конденсаторе в большинстве случаев пренебрегают и собственные потери контура представляют сопротивлением
а б
Для исследования временных характеристик параллельного контура источник напряжения u(t) (рис. 4.2, а) заменяют источником тока Импульсной реакцией, или импульсной характеристикой, параллельного колебательного контура принято называть напряжение Здесь Из выражений (4.3) и (4.9) следует, что
а б
Из выражения (4.6) следует, что при безразмерном где
Снизить влияние сопротивлений При подключении источника напряжения u(t) к части индуктивной ветви контура он может быть заменен генератором тока где
3. Описание лабораторной установки
Макет установки (рис. 4.5) включает в себя исследуемые частотно-избирательные цепи с согласующими каскадами и коммутирующие элементы.
Рис. 4.5
На вход макета подают прямоугольные видеоимпульсы — для исследования временных функций и гармонические сигналы — для исследования АЧХ. Поскольку выходное сопротивление используемых генераторов довольно большое (десятки или сотни Ом), они подключаются к исследуемым цепям через согласующий каскад с низким выходным сопротивлением. На параллельный контур сигнал подается через большое сопротивление Выходной каскад имеет высокое входное и низкое выходное сопротивления при коэффициенте передачи, равном единице. Этот каскад исключает влияние измерительных приборов на исследуемые цепи. В макете предусмотрены переключатель вида контура (последовательный — параллельный) и два активных сопротивления нагрузки. Одно ( 4. Методика выполнения работы
Включить питание макета и используемых приборов. Установить конденсатор переменной емкости в среднее положение, нагрузочный резистор отключить от контура. Для исследования импульсных характеристик к входу макета подключить выход генератора импульсов, к выходу — вход «Y» осциллографа. Для измерения частотных характеристик использовать высокочастотный генератор синусоидальных сигналов и вольтметр переменного тока. Исследование импульсных характеристик колебательных контуров 1. Установить генератор прямоугольных импульсов в положение внутреннего запуска, нажав клавишу «Запуск». Длительность импульса возбуждения цепи t = 0,1…0,3 мкс, частота повторения импульсов 3×105 Гц, амплитуда импульсовоколо 10 В (выход генератора 1:1, множитель — 0,3). 2. Подать синхроимпульс положительной полярности от выхода синхронизации генератора импульсов на вход внешней синхронизации осциллографа. Установить на экране осциллографа, работающего в ждущем режиме, неподвижное изображение реакции цепи на входной импульс. Для этого отрегулировать уровень синхронизации. 3. Измерения начать с исследования импульсной реакции последовательного контура без добавочного резистора r (он должен быть замкнут переключателем). Резистор нагрузки R н при этом должен быть отключен. Подобрать коэффициент отклонения K 0, В/дел в канале «Y» и коэффициент развертки K р, мкс/дел в канале «X» так, чтобы осциллограмма импульсной реакции занимала бы большую часть экрана. 4. Измерить параметры импульсной реакции (постоянную времени контура tк и длительность квазипериода колебаний T). Постоянную времени tк определить в виде интервала времени, в течение которого огибающая импульсной реакции уменьшится в е = 2,72… раз. Для этого: а) найти сечение огибающей б) оценить длительность квазипериода колебаний: выбрать на экране достаточно большой временной интервал и подсчитать количество квазипериодов, укладывающихся в него. Разделив интервал на полученное число, найти квазипериод Т и значение резонансной частоты f р = 1/ Т. 5. Включить добавочный резистор r. При этом добротность контура снизится, и постоянная времени импульсной реакции уменьшится. Измерить 6. Переключить макет в режим параллельного контура и измерить постоянную времени аналогичным образом. Затем исследовать влияние сопротивления нагрузки R на постоянную времени контура. Для этого установить переменный резистор в среднее положение, подключить нагрузку к полному контуру и измерить tк. Повторить измерения для частичного включения нагрузки в индуктивную и емкостную ветви контура. 7. Результаты измерений (6 значений постоянной времени) свести в таблицу. Исследование частотных характеристик колебательных контуров 1. Подключить к входу макета высокочастотный генератор, выбрать диапазон частот в районе 200….600 кГц. Установить режим непрерывной генерации (отсутствие модуляции). 2. К выходу макета подключить вольтметр, установить шкалу вольтметра 1 В. 3. Измерить резонансную частоту и полосу пропускания контура по уровню 0,707 от максимума. Для этого: а) определить максимум АЧХ и зафиксировать по шкале генератора значение резонансной частоты f p; б) подобрать амплитуду генератора так, чтобы выходное напряжение составило бы на резонансной частоте 1 В; в) плавно перестраивая генератор в обе стороны от резонансной частоты, найти точки f 0,707, где выходное напряжение равняется 0,707 В, и зафиксировать эти частоты. Модуль их разности и есть полоса пропускания контура. 4. Измерить резонансные частоты и полосы пропускания последовательного и параллельного контуров для случаев, указанных в п. 3. Результаты свести в таблицу. Расчет добротности колебательных контуров 1. Используя данные измерений постоянных времени и резонансных частот контуров, по формуле 2. По полученным данным рассчитать сопротивления нагрузки, подключенные к контуру. Для последовательного контура определить дополнительное сопротивление r н, полагая, что в первом варианте (с закороченным r н) найдена собственная добротность Q 0, а во втором — нагруженная добротность контура Q н. 3. Используя вытекающее из (4.4) соотношение и указанное на макете значение индуктивности, рассчитать значение добавочного сопротивления r н. 4. Провести аналогичные расчеты сопротивления нагрузки для параллельного контура. Расчетные формулы для этого вывести, используя результаты первого измерения как данные о собственной, а второго — нагруженной добротности. 5. Содержание отчета
Отчет по лабораторной работе должен содержать схемы исследуемых цепей, таблицы с данными измерений постоянных времени, резонансных частот и полос пропускания контуров, а также результаты расчетов и графики импульсной и амплитудно-частотной характеристик для одного из контуров.
Литература: [1], с. 218-222; [2], с. 190-193 Лабораторная работа 5
|
|||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

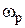 он обладает низким входным сопротивлением и для обеспечения колебательного режима должен подключаться к источнику сигнала с достаточно малым выходным сопротивлением
он обладает низким входным сопротивлением и для обеспечения колебательного режима должен подключаться к источнику сигнала с достаточно малым выходным сопротивлением 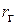 таким, чтобы выполнялось условие
таким, чтобы выполнялось условие 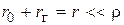 , где
, где 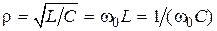 — волновое, или характеристическое, сопротивление контура.
— волновое, или характеристическое, сопротивление контура.
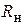 >> r), запишем дифференциальное уравнение для выходного напряжения четырехполюсника
>> r), запишем дифференциальное уравнение для выходного напряжения четырехполюсника 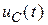 :
: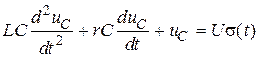 , (4.1)
, (4.1)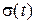 (функция Хевисайда). Однородному дифференциальному уравнению
(функция Хевисайда). Однородному дифференциальному уравнению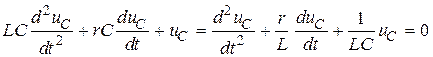 (4.2)
(4.2)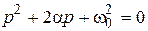
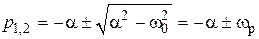 ; здесь a = r/(2L),
; здесь a = r/(2L), 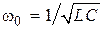 («собственная» резонансная частота контура). Решение неоднородного дифференциального уравнения (4.1) ищут в виде суммы решения однородного уравнения (4.2) и так называемого частного решения уравнения (4.1), которое при выбранном входном воздействии оказывается просто константой U:
(«собственная» резонансная частота контура). Решение неоднородного дифференциального уравнения (4.1) ищут в виде суммы решения однородного уравнения (4.2) и так называемого частного решения уравнения (4.1), которое при выбранном входном воздействии оказывается просто константой U: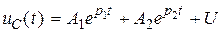 .
. , i(0) = 0, находят константы
, i(0) = 0, находят константы 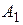 и
и 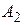 и записывают решение:
и записывают решение: ,
,
 , t ³ 0. (4.3)
, t ³ 0. (4.3)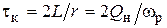 последовательного колебательного контура. Здесь
последовательного колебательного контура. Здесь 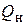 — нагруженная добротность контура, определяемая соотношением
— нагруженная добротность контура, определяемая соотношением . (4.4)
. (4.4)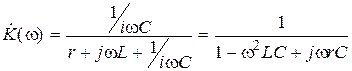 =
= 
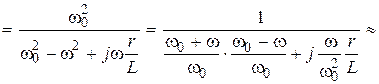

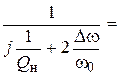
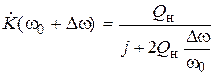
 . (4.5)
. (4.5)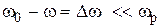 ,
, 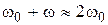 — в приближении малых расстроек.
— в приближении малых расстроек.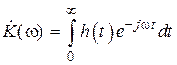 . (4.6)
. (4.6)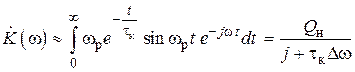 .
. ,
, 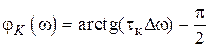 . (4.7)
. (4.7) = r. Поэтому последовательные контуры часто используют как режекторные фильтры для подавления сигнала на резонансной частоте.
= r. Поэтому последовательные контуры часто используют как режекторные фильтры для подавления сигнала на резонансной частоте.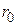 , отнесенным к индуктивности. Для удобства анализа схемы последовательное соединение
, отнесенным к индуктивности. Для удобства анализа схемы последовательное соединение 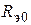 и L, пренебрегая квадратом сопротивления потерь
и L, пренебрегая квадратом сопротивления потерь  по сравнению с квадратом индуктивного сопротивления, (
по сравнению с квадратом индуктивного сопротивления, ( L)2 >>
L)2 >>  , где r, как и для последовательного контура, — волновое, или характеристическое, сопротивление, равное сопротивлению одной ветви контура на резонансной частоте,
, где r, как и для последовательного контура, — волновое, или характеристическое, сопротивление, равное сопротивлению одной ветви контура на резонансной частоте, 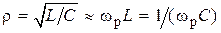 ;
; 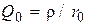 — собственная (ненагруженная) добротность колебательной системы. Для сохранения в контуре колебательного режима добротность должна быть достаточно велика, следовательно, подключаемые к нему сопротивления источника сигнала (генератора)
— собственная (ненагруженная) добротность колебательной системы. Для сохранения в контуре колебательного режима добротность должна быть достаточно велика, следовательно, подключаемые к нему сопротивления источника сигнала (генератора) 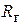 и нагрузки
и нагрузки 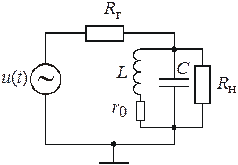
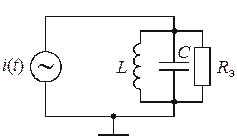
 , а параллельно подключенные к контуру сопротивления
, а параллельно подключенные к контуру сопротивления 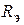 (рис. 4.2, б) в соответствии с равенством
(рис. 4.2, б) в соответствии с равенством 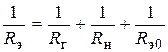 , где
, где 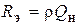 ,
, 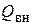 , которая связывает собственную и нагруженную добротности
, которая связывает собственную и нагруженную добротности 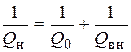 .
.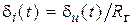 (при экспериментальном определении импульсной характеристики используют достаточно короткий импульс). Импульсная реакция параллельного контура имеет колебательный характер и может быть записана как
(при экспериментальном определении импульсной характеристики используют достаточно короткий импульс). Импульсная реакция параллельного контура имеет колебательный характер и может быть записана как
 . (4.8)
. (4.8)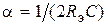 . Приближение (4.8) с учетом того, что α - мало и ωр≈ω0 (напомним, что
. Приближение (4.8) с учетом того, что α - мало и ωр≈ω0 (напомним, что  , где
, где 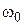 — «собственная» резонансная частота контура), принимают для высокодобротного контура. Вводят также понятие постоянной времени
— «собственная» резонансная частота контура), принимают для высокодобротного контура. Вводят также понятие постоянной времени  нагруженного параллельного контура и записывают выражение (4.8) в форме
нагруженного параллельного контура и записывают выражение (4.8) в форме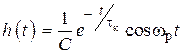 ,
, 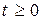 . (4.9)
. (4.9)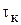 является интервалом времени между точками, соответствующими спаду огибающей импульсной характеристики в e = 2,72… (основание натуральных логарифмов) раз.
является интервалом времени между точками, соответствующими спаду огибающей импульсной характеристики в e = 2,72… (основание натуральных логарифмов) раз.

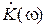 размерностью h (t) является 1/с. При определении импульсной характеристики параллельного колебательного контура было принято воздействие в виде дельта-импульса тока, а в качестве реакции — напряжение на контуре, поэтому размерностью
размерностью h (t) является 1/с. При определении импульсной характеристики параллельного колебательного контура было принято воздействие в виде дельта-импульса тока, а в качестве реакции — напряжение на контуре, поэтому размерностью 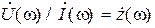 , — а размерностью h (t) будет Ом/с = 1/Ф, что поясняет присутствие в выражениях (4.8) и (4.9) множителя 1/ С. Комплексный коэффициент передачи параллельного колебательного контура записывается как
, — а размерностью h (t) будет Ом/с = 1/Ф, что поясняет присутствие в выражениях (4.8) и (4.9) множителя 1/ С. Комплексный коэффициент передачи параллельного колебательного контура записывается как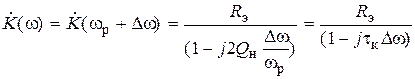 , (4.10)
, (4.10)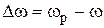 — абсолютная расстройка, как и для последовательного колебательного контура. Можно показать, что если
— абсолютная расстройка, как и для последовательного колебательного контура. Можно показать, что если 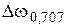 — полоса заграждения контура на уровне 0,707 от максимума АЧХ, то
— полоса заграждения контура на уровне 0,707 от максимума АЧХ, то  — добротность контура, практически совпадающая с нагруженной добротностью контура, определенной через временные характеристики. Из выражения (4.10) определяют АЧХ и ФЧХ цепи (рис. 4.3, б):
— добротность контура, практически совпадающая с нагруженной добротностью контура, определенной через временные характеристики. Из выражения (4.10) определяют АЧХ и ФЧХ цепи (рис. 4.3, б):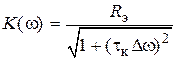 ,
, 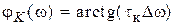 . (4.11)
. (4.11)
 ,
, 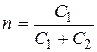 .
.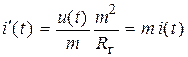 , подключенным к контуру вида рис. 4.2, б. В этом случае комплексная частотная характеристика приобретает вид
, подключенным к контуру вида рис. 4.2, б. В этом случае комплексная частотная характеристика приобретает вид ,
, — эквивалентная нагруженная добротность,
— эквивалентная нагруженная добротность, 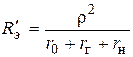 — эквивалентное сопротивление контура с учетом собственных и внешних потерь,
— эквивалентное сопротивление контура с учетом собственных и внешних потерь, 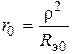 — собственные потери контура (от коэффициентов включения не зависят),
— собственные потери контура (от коэффициентов включения не зависят), 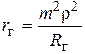 ,
, 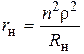 — пересчитанные с учетом частичного включения сопротивления генератора и нагрузки. Подбором коэффициентов включения удается обеспечить требуемую полосу пропускания контура и расчетное эквивалентное сопротивление. Это особенно важно при использовании параллельного контура в качестве нагрузки в резонансных усилителях и генераторах.
— пересчитанные с учетом частичного включения сопротивления генератора и нагрузки. Подбором коэффициентов включения удается обеспечить требуемую полосу пропускания контура и расчетное эквивалентное сопротивление. Это особенно важно при использовании параллельного контура в качестве нагрузки в резонансных усилителях и генераторах.
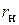 ) предназначено для включения в последовательный контур. Второе (переменный резистор
) предназначено для включения в последовательный контур. Второе (переменный резистор 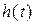 по уровню 1/ е от максимума и подсчитать количество делений экрана, укладывающееся между максимумом и найденным сечением, умножив его на коэффициент развертки K р, получить значение
по уровню 1/ е от максимума и подсчитать количество делений экрана, укладывающееся между максимумом и найденным сечением, умножив его на коэффициент развертки K р, получить значение 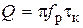 рассчитать собственную и нагруженную добротности параллельного и последовательного контуров. Используя результаты измерений полос пропускания и резонансных частот контуров, по формуле
рассчитать собственную и нагруженную добротности параллельного и последовательного контуров. Используя результаты измерений полос пропускания и резонансных частот контуров, по формуле 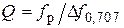 рассчитать эквивалентные добротности контуров. Сопоставить результаты расчетов.
рассчитать эквивалентные добротности контуров. Сопоставить результаты расчетов.