
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез сигналов по дискретным отсчетам котельникова
1. Цель работы – изучение возможности синтезирования сигналов по дискретным отсчетам в соответствии с теоремой Котельникова, исследование влияния частоты выборок и характеристик фильтров нижних частот на качество синтезирования.
2. Основные теоретические положения В соответствии с теоремой Котельникова сигнал s (t), не содержащий частот выше Fm, полностью определяется своими мгновенными значениями s (n D t), отсчитанными через интервалы времени
Отсчеты сигнала s (t) в моменты времени n D t являются коэффициентами Фурье
Спектральное пояснение теоремы Котельникова дает рис 7.1, на котором изображены исходный сигнал s (t) (рис. 7.1, а), его спектр
и их спектры
для различных частот выборок Спектр выборочного сигнала представляет собой сумму копий спектра сигнала s (t) с центральными частотами 0,
Импульсная характеристика такого фильтра с точностью до постоянного множителя совпадает с функцией отсчетов
Если же При практическом использовании теоремы Котельникова для восстановления спектра сигналов по отсчетам необходимо учитывать неизбежно возникающие погрешности. Причины для этого следующие.
Рис. 7.1 На рис. 7.1 изображены сигналы и их спектры, где а – сигнал s (t); б – выборочный сигнал 1. Сигналы с ограниченным спектром бесконечны во времени, и поэтому восстановление мгновенного значения s (t) принципиально требует учета значений бесчисленного множества дискретных отсчетов. Использование отсчетов, взятых в ограниченном интервале (0, Т), означает переход к конечным пределам
2. Сигналы конечной длительности имеют бесконечные частотные спектры. В этом случае 3. Отклонение характеристик реальных фильтров нижних частот от идеальных (7.4 и 7.5) приводит к появлению дополнительных погрешностей восстановления сигнала s (t) по отсчетам Котельникова.
3. Описание лабораторной установки В сменном устройстве находятся матричный генератор двадцати отсчетных импульсов, потенциометры установки полярности и амплитуд отсчетных импульсов, сумматор, два фильтра нижних частот с граничными частотами 5 кГц, тумблер «Синтез» – «Измерение частотной характеристики фильтра», тумблер «Фильтр НЧ – 1» – «Фильтр НЧ – 2» и схема, вырабатывающая импульс синхронизации. Вид передней панели сменного функционального устройства показан на рис.7.2. Гнезда Г2 служат для измерения частотной характеристики фильтра.
Рис.7.2
Запуск генератора отсчетных импульсов осуществляется синусоидальным сигналом внешнего лабораторного генератора, подключаемого к гнездам Г1; при этом частота следования отсчетных импульсов (частота выборок Этот же внешний генератор используется для измерения частотных характеристик фильтров НЧ; в этом случае он должен быть подключен к гнездам Г2. Сигнал с выхода ФНЧ (первого или второго в зависимости от положения соответствующего тумблера) поступает па гнезда Г3. Сигнал, действующий на входе фильтров (выборочный при синтезе и синусоидальный при измерении частотных характеристик), поступает на гнезда Г4. К гнездам Г5 подается импульсный сигнал для внешней синхронизации осциллографа.
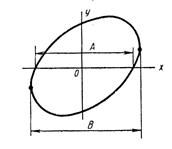
4. Методика выполнения работы 1. Снять амплитудно-частотные и фазочастотные характеристики LC и RC – фильтров нижних частот 1 и 2 в диапазоне частот 200 Гц ¸ 10 кГц при 1.1. Подготовить лабораторный генератор, вольтметр, осциллограф и лабораторную установку к работе. Установить выходное сопротивление лабораторного генератора равным 5 Ом, выходное напряжение – 1 В, включить внутреннюю нагрузку генератора. Тумблер «Синтез – Измерение частотных характеристик фильтра» на установке поставить в положение «Измерение частотных характеристик фильтра». 1.2. Собрать схему исследования. Подключить генератор к гнездам Г2 лабораторной установки, входы «У» и «X» осциллографа подсоединить к гнездам ГЗ и Г4, вольтметр подключить к входным клеммам усилителя вертикального отклонения осциллографа. Выключить развертку осциллографа. 1.3. Снять зависимости Установить частоты 200 Гц, 1, 2, 3,..., 10 кГц. Для каждого значения частоты фиксировать по вольтметру значения U вых, а по фигуре Лиссажу на экране осциллографа (рис. 7.3) – значения А и В.
Рис. 7.3
Фазовый сдвиг между напряжениями на входе и выходе фильтра
Так как Рекомендуется измерения частотных характеристик фильтров НЧ 1 и 2 производить одновременно. 2. Получить и зарисовать осциллограммы импульсных характеристик фильтров НЧ 1 и 2. 2.1. Собрать схему исследования. Подключить лабораторный генератор к гнездам Г1, установить выходное напряжение генератора Тумблер «Синтез – Измерение частотных характеристик фильтра» поставить в положение «Синтез». Вход усилителя вертикального отклонения осциллографа подключить к гнездам Г4. Для внешней синхронизации осциллографа использовать импульсы, снимаемые с гнезд Г5. 2.2. Установить масштаб горизонтальной развертки 20 мкс/мм. Получить на экране осциллографа устойчивую осциллограмму 20-ти выборочных импульсов. Отрегулировать усиление канала X осциллографа так, чтобы интервалу между соседними выборками 2.3. Установить амплитуду первого отсчетного импульса положительной полярности максимальной, а амплитуды остальных импульсов равными нулю. Заметить положение на экране первого отсчетного импульса. 2.4. Подключить вход усилителя Y -канала осциллографа к гнездам ГЗ, усиление Y -канала увеличить в 10 раз. Наблюдать импульсные характеристики фильтров, обратив внимание на временные сдвиги осциллограмм относительно импульса, действующего на входах ФНЧ. Зарисовать осциллограммы. 3. Синтезировать сигналы, перечисленные в домашнем задании. Зарисовать осциллограммы всех выборочных (гнезда Г4) и синтезированных сигналов (гнезда ГЗ) на выходе фильтров НЧ 1 и 2. 3.1. Во всех случаях, регулируя усиление Х -канала, установить масштаб горизонтальной развертки одинаковым и равным 20 мкс/мм. 3.2. Установить рассчитанные значения амплитуд отсчетных импульсов по осциллографу, подключив его ко входу фильтра – к гнездам Г4. 3.3. Подключить осциллограф к гнездам ГЗ. Наблюдать синтезированные сигналы на выходе ФНЧ 1 и 2. Зарисовать осциллограммы, обращая внимание на временные сдвиги синтезированных сигналов относительно выборочных.
5. Содержание отчета
Отчет должен содержать: 1) функциональную схему устройства для синтеза сигналов по дискретным отсчетам Котельникова; 2) частотные и импульсные характеристики ФНЧ 1 и 2 и идеального ФНЧ; 3) графики всех выборочных сигналов; 4) осциллограммы всех выборочных и синтезированных сигналов в одинаковом временном масштабе; 5) спектры выборочных сигналов; 6) выводы и оценку полученных результатов.
Литература: [1], с. 116 – 120; [2], с. 74-78
Лабораторная работа 8
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.59.231 (0.014 с.) |
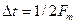 :
: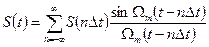 . (7.1)
. (7.1)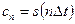 разложения сигнала s (t) по ортогональной системе функций отсчета:
разложения сигнала s (t) по ортогональной системе функций отсчета: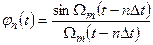 .
.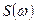 (рис. 7.1, д), выборочные сигналы
(рис. 7.1, д), выборочные сигналы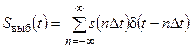 (7.2)
(7.2)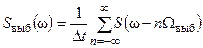 (7.3)
(7.3)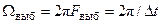 .
.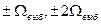 и т. д. Если
и т. д. Если 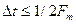 , т. е.
, т. е. 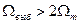 , то можно восстановить исходный сигнал s (t), пропустив выборочный сигнал (7.2) через идеальный фильтр нижних частот (ФНЧ) с комплексным коэффициентом передачи:
, то можно восстановить исходный сигнал s (t), пропустив выборочный сигнал (7.2) через идеальный фильтр нижних частот (ФНЧ) с комплексным коэффициентом передачи: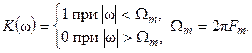 (7.4)
(7.4)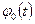 :
: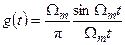 . (7.5)
. (7.5)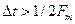 , т. е.
, т. е. 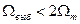 , то соседние копии спектра перекрываются и восстановление сигнала s (t) невозможно. Минимальный интервал (период) выборок равен
, то соседние копии спектра перекрываются и восстановление сигнала s (t) невозможно. Минимальный интервал (период) выборок равен 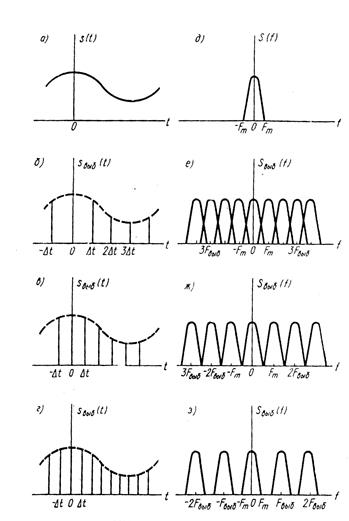
 при
при  ; в –
; в –  ; г –
; г – 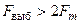 ; д – спектр
; д – спектр 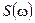 сигнала s (t); е – спектр выборочного сигнала
сигнала s (t); е – спектр выборочного сигнала 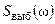 при
при 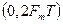 в ряде (7.1) и вызывает появление ошибки восстановления.
в ряде (7.1) и вызывает появление ошибки восстановления.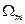 обычно выбирают так, чтобы в диапазоне частот от нуля до
обычно выбирают так, чтобы в диапазоне частот от нуля до 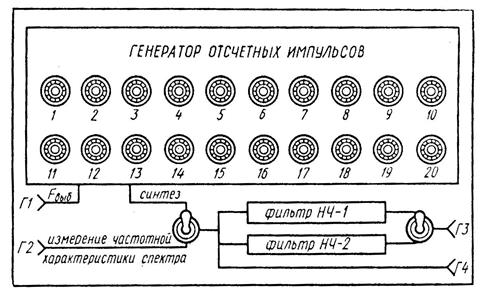
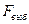 ) равна частоте внешнего генератора, а временной интервал между отсчетными импульсами –
) равна частоте внешнего генератора, а временной интервал между отсчетными импульсами – 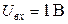 . Определить граничные частотные фильтры на уровне 0,5 (см. рис. 7.2).
. Определить граничные частотные фильтры на уровне 0,5 (см. рис. 7.2).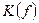 и
и 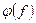 .
.
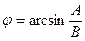 . (7.6)
. (7.6)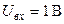 , выходное напряжение фильтра, измеряемое вольтметром, численно равно модулю коэффициента передачи фильтра.
, выходное напряжение фильтра, измеряемое вольтметром, численно равно модулю коэффициента передачи фильтра.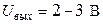 и частоту
и частоту 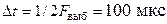 на экране осциллографа соответствовало расстояние по оси х, равное 5 мм.
на экране осциллографа соответствовало расстояние по оси х, равное 5 мм.


