
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоретические положения. Случайные сигналы могут быть стационарными и нестационарными.
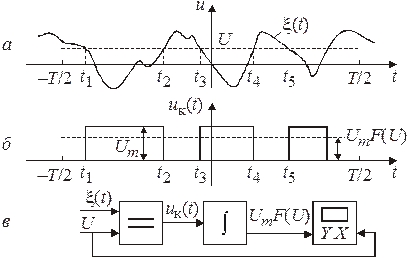
Случайные сигналы могут быть стационарными и нестационарными. Для стационарного сигнала усредненные характеристики не зависят от выбора начального отсчета времени. В данной работе рассматриваются стационарные сигналы. Основной характеристикой случайных сигналов являются функции распределения вероятностей их значений. По функциям распределения могут быть определены все другие характеристики сигнала, в том числе его среднее значение, дисперсия, корреляционная функция, вероятность попадания в заданный интервал значений. Одномерная функция распределения вероятностей F (U) случайного сигнала x(t) есть вероятность того, что значение сигнала не превысит уровень U: F (U) = P (x £ U). Основные свойства функции F (U): 1. 0 £ F (U) £ 1, причем F (–¥) = 0, F (¥) = 1; 2. 3. Для функции распределения F (U), имеющей производную, вводят понятие плотности вероятностей: Основные свойства функции p (U). 4. Размерность p (U) равна обратной величине размерности случайного сигнала 5. p (U) ³ 0; 6. Функция распределения определяется выражением 7. Вероятность попадания случайной величины в интервал Для исследуемых в работе сигналов предполагается выполнение условия эргодичности. Из него следует, что средние параметры случайного процесса, определенные по множеству реализаций, с единичной вероятностью равны средним параметрам, определенным по одной реализации. Для таких сигналов одномерная функция распределения F (U) равна отношению времени, в течение которого значения сигналов не превышают заданный уровень U ко всему времени T измерения сигнала (3.2) (рис. 3.1, а): Указанное свойство используется в измерительном приборе для измерения функции распределения. Структурная схема измерителя приведена на рис. 3.1, в. Опорное напряжение U и случайный сигнал x(t) подаются на два входа компаратора (сравнивающего устройства). Если x(t) > U, напряжение на выходе компаратора равно нулю, а при x(t) £ U оно равно
Выход компаратора соединен с интегратором, выполненным в виде RC ‑цепи. При D f RC >> 1, где D f — ширина спектра случайного сигнала, напряжение на выходе компаратора равно
Рис. 3.1
Напряжение с выхода интегратора подается на вход «Y» осциллографа, а опорное напряжение на вход «Х». При медленном изменении опорного напряжения U на экране осциллографа появляется изображение F (U) — функции распределения вероятностей значений исследуемого случайного сигнала x(t). Метод измерения плотности вероятности основан на формуле численного дифференцирования функции Если D U мало и постоянно, то p (U) пропорционально разности F (U + D U) – F (U), т. е. разности напряжений на выходах двух измерителей функции распределения сигналов x(t) при опорных напряжениях U + D U и U соответственно на первом и втором измерителях (рис. 3.2).
Рис. 3.2 В работе исследуются функции распределения и плотности вероятности для следующих случайных сигналов. Треугольный сигнал со случайной начальной фазой (рис. 3.3, а). Он имеет равномерное распределение вероятностей значений напряжения (рис. 3.3, б, в), описываемое следующими выражениями:
Рис. 3.3
Шум усилителя. Он имеет гауссовскую функцию распределения (рис. 3.4, а, б). Для него где
Рис. 3.4
Напряжение x(t) на выходе амплитудного детектора. На вход детектора подается сумма двух сигналов: узкополосного шума Напряжение x(t) имеет функцию распределения, соответствующую обобщенному закону Рэлея (рис. 3.5, а, б): где
При
Рис. 3.5
Гармонический сигнал с постоянной амплитудой и случайной фазой Найдем функцию распределения напряжения случайного сигнала x(t). Это стационарный сигнал, поэтому можно положить t = 0. Тогда Используя определение функции распределения и выражение (3.6), последнее равенство можно записать в виде
для Из рис. 3.6, авидно также, что Плотность распределения вероятностей значений x:
Графики функций Согласно центральной предельной теореме теории вероятностей функция распределения суммы независимых случайных величин с близкими значениями дисперсий стремится к гауссовскому закону распределения при увеличении числа слагаемых, независимо от вида функций распределения слагаемых. Аналитическое выражение для функции распределения суммы сигналов удобно получать через характеристическую функцию.
Рис. 3.6
Характеристическая функция q(x) сигнала x(t) связана с плотностью распределения вероятностей p (x) преобразованием Фурье: Для суммы случайных величин Для независимых случайных величин а потому где Последовательное использование зависимостей (3.10), (3.9) и (3.8) позволяет получить плотность распределения вероятностей суммы независимых сигналов по известным плотностям распределения отдельных слагаемых. Найдем распределение суммы двух независимых случайных сигналов с одинаковым равномерным распределением. Пусть Характеристические функции сигналов Согласно выражению (3.10) характеристическая функция суммы сигналов Плотность распределения вероятностей суммы сигналов
Зависимости
Рис. 3.7
Рис. 3.8 Для сигнала Графики зависимостей p (x) приведены на рис. 3.8. Видно, что с увеличением числа слагаемых плотность распределения их суммы стремится к гауссовскому распределению (ср. с рис. 3.4 при
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.82.79 (0.051 с.) |
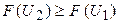 при
при 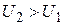 , т. е. F (U) — неубывающая функция;
, т. е. F (U) — неубывающая функция;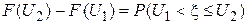 — вероятность попадания случайного сигнала x(t) в полузакрытый интервал
— вероятность попадания случайного сигнала x(t) в полузакрытый интервал 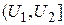 .
.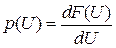 . (3.1)
. (3.1)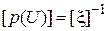 ;
;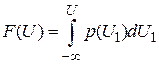 ; (3.2)
; (3.2)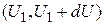 равна
равна 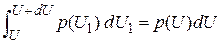 .
.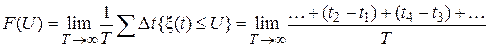 .
.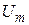 (рис. 3.1, б).
(рис. 3.1, б).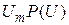 .
.
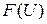 (3.1):
(3.1):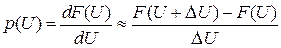 для малых D U.
для малых D U.
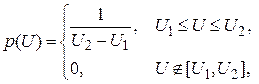
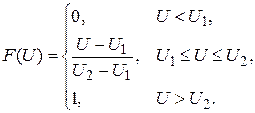 (3.3)
(3.3)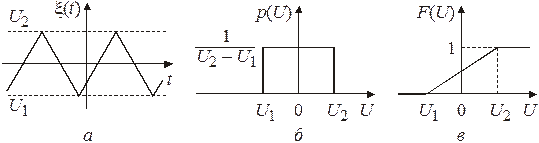
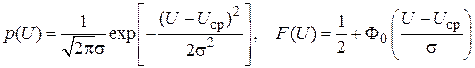 , (3.4)
, (3.4)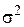 — дисперсия,
— дисперсия, 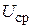 — среднее значение напряжения,
— среднее значение напряжения, 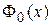 — интеграл ошибок, значения которого табулированы.
— интеграл ошибок, значения которого табулированы.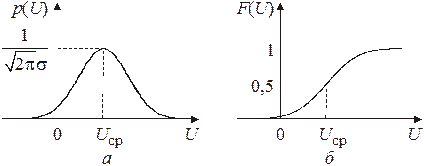
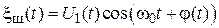 с гауссовским законом распределения вероятностей значений
с гауссовским законом распределения вероятностей значений 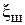 и детерминированного гармонического сигнала
и детерминированного гармонического сигнала 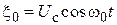 с постоянной амплитудой
с постоянной амплитудой 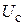 ; x(t) — огибающая суммы этих двух сигналов.
; x(t) — огибающая суммы этих двух сигналов.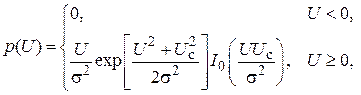 (3.5)
(3.5)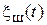 ,
, 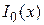 — модифицированная функция Бесселя нулевого порядка. Она табулирована; кроме того,
— модифицированная функция Бесселя нулевого порядка. Она табулирована; кроме того, 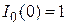 ;
; 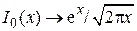 при x ® ¥.
при x ® ¥.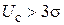 обобщенное распределение Рэлея приближается к гауссовскому распределению (рис. 3.5, а, б).
обобщенное распределение Рэлея приближается к гауссовскому распределению (рис. 3.5, а, б).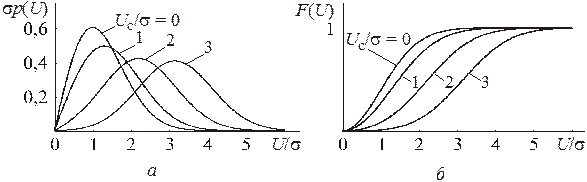
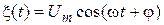 , где
, где 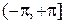 , т. е. плотность распределения фазы
, т. е. плотность распределения фазы 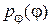 и функция распределения фазы
и функция распределения фазы 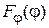 имеют вид
имеют вид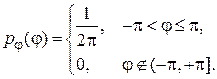
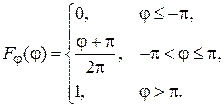 (3.6)
(3.6)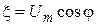 . Из графика функции x(j) (рис. 3.6, а) видно, что вероятность события
. Из графика функции x(j) (рис. 3.6, а) видно, что вероятность события 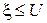 (для
(для 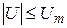 ) равна вероятности события
) равна вероятности события 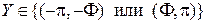 , где
, где 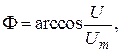 т. е.
т. е. 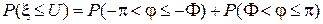 .
.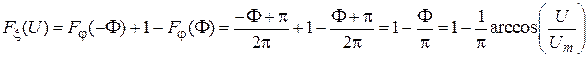
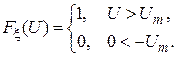
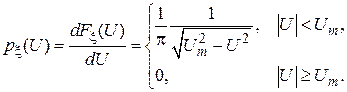 (3.7)
(3.7)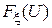 и
и 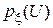 приведены на рис. 3.6, би 3.6, в.
приведены на рис. 3.6, би 3.6, в.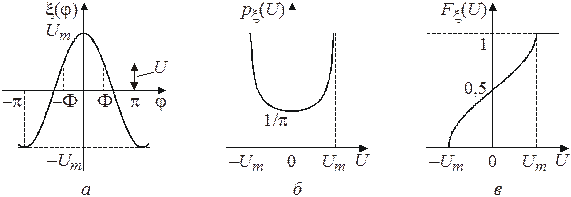
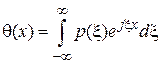 ;
; 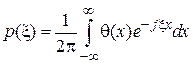 . (3.8)
. (3.8)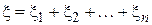 характеристическая функция связана с совместной плотностью распределения вероятностей величин
характеристическая функция связана с совместной плотностью распределения вероятностей величин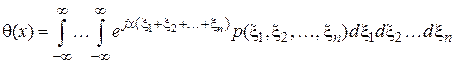 .
.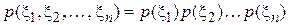 , (3.9)
, (3.9)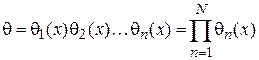 , (3.10)
, (3.10)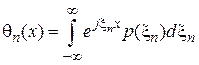 — характеристическая функция сигнала
— характеристическая функция сигнала 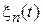 .
.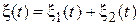 , где
, где 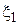 и
и 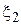 — независимые случайные сигналы с плотностями распределения вероятностей
— независимые случайные сигналы с плотностями распределения вероятностей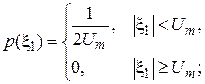
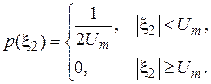
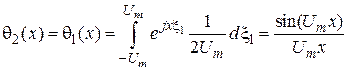 .
.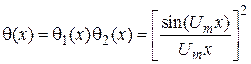 .
.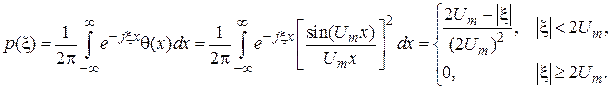
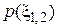 и p (x) приведены на рис. 3.7.
и p (x) приведены на рис. 3.7.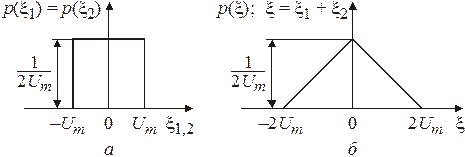
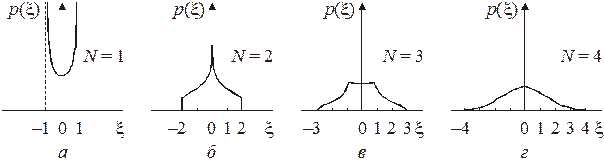
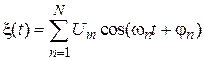 в виде суммы гармонических колебаний с равными амплитудами
в виде суммы гармонических колебаний с равными амплитудами 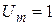 и независимыми случайными фазами
и независимыми случайными фазами 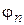 , распределенными в интервале
, распределенными в интервале 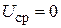 ).
).


