Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение спектральной плотности для различных сигналов
1. Определить спектр сигнала, указанного на графике, и построить его спектральную диаграмму.
Определяем коэффициенты ряда Фурье, учитывая, что сигнал нечетный:
В данном случае s (t) = V, тогда
Определяем допустимые значения s (t):
После интегрирования получим
Теперь записываем ряд Фурье:
Построим график:
2. Вычисление спектра непериодического сигнала (импульса).
На графике показан одиночный импульс, являющийся четной функцией, так как s (- t) = s (t). Данная функция имеет два параметра: V – амплитуда импульса; Импульс описывается следующим образом:
Вычисляем спектральную плотность по формуле
Удобнее записать:
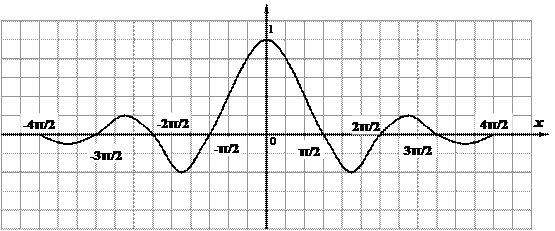
Функция sinc(x) примечательна тем, что для нее выполняются условия:
sinc(0) = 1; sinc(n π) = 0.
Тогда можно записать, что спектральная плотность - это знакопеременная действительная функция.
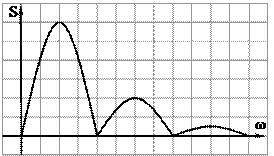
Как видно из графика, спектральная плотность импульса – это четная функция, имеющая лепестковую структуру. Изобразим амплитудный и фазовый спектры на графике:
Амплитудный спектр можно определить из выражения
Как видно из графика, амплитудный спектр – это четная функция, имеющая лепестковую структуру. Ширина лепестка равна 2π/τи=Δω. Чем шире импульс, тем уже спектр. График фазового спектра можно объяснить следующим образом. Поскольку спектральная плотность является знакопеременной функцией, а изменение знаков функции равносильно изменению фазы на
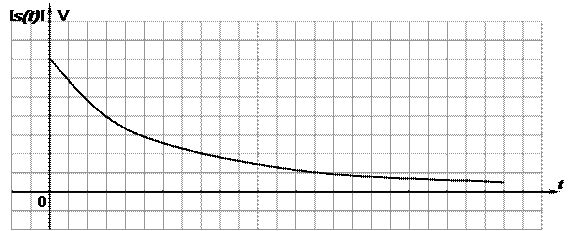
3. Вычисление спектра экспоненциального импульса.
Импульс описывается формулой
Вычислим спектральную плотность:
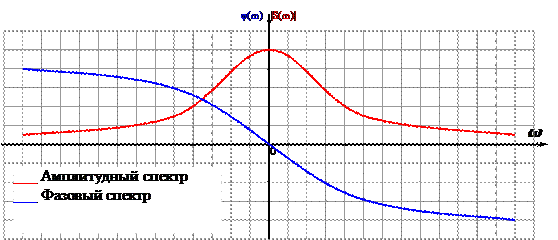
Эта функция комплексная, определим амплитудный и частотный спектры:
Построим графики этих спектров:
4. Определить спектральную плотность
1) 2) Объединим спектры в один общий:
т.к.
На нулевой частоте амплитудный спектр будет равен нулю.
Литература: [1] с. 38 – 51; [2], с. 50 – 58 Практическое занятие № 2 Определение корреляционных функций для детерминированных Сигналов 1. Определить корреляционную функцию прямоугольного импульса.
Найти автокорреляционную функцию (АКФ). Аналогично для
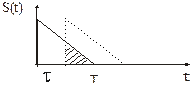
2. Определить корреляционную функцию пилообразного импульса.
Найти АКФ.
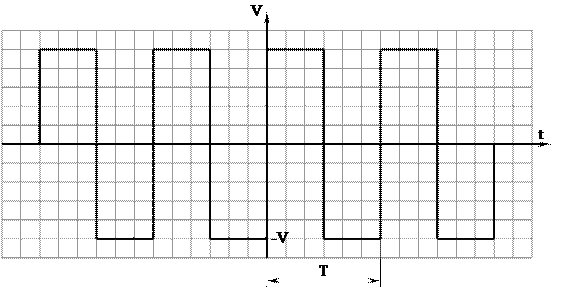
3.Определить корреляционную функцию экспоненциального импульса
Найти АКФ. Литература: [1] с. 73 – 79; [2], с. 79 - 84 Практическое занятие № 3
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.178.240 (0.014 с.) |
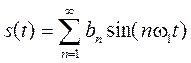 ,
,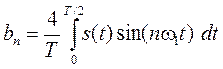 .
.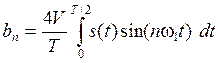 .
.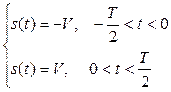 .
.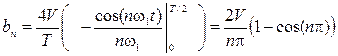 ,
,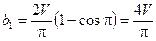 ,
,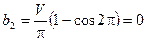 ,
,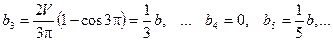
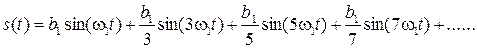
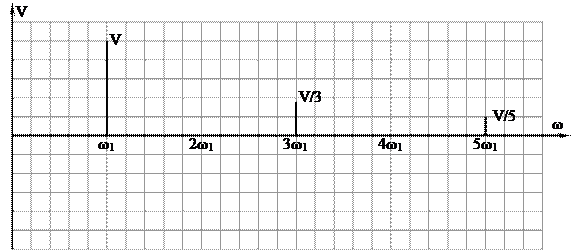 Покажем полученный результат на спектральной диаграмме:
Покажем полученный результат на спектральной диаграмме: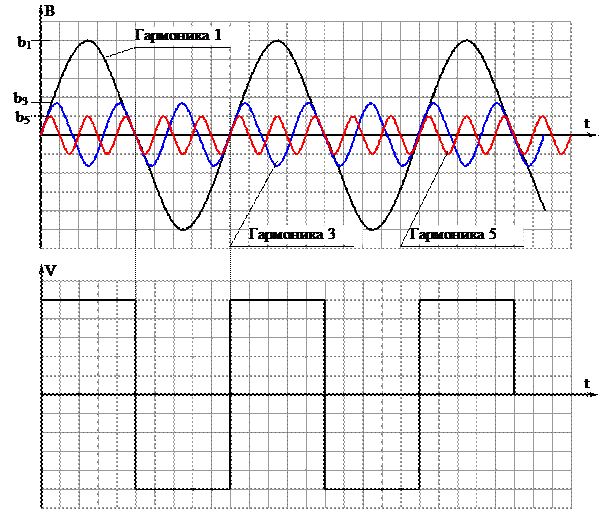
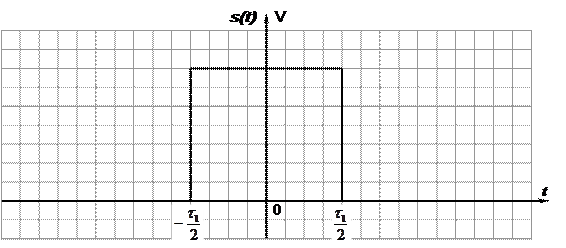
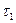 - длительность импульса.
- длительность импульса.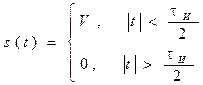 .
. 
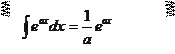
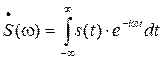
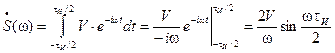 .
.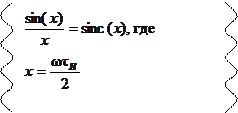
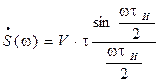 .
.
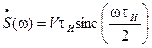
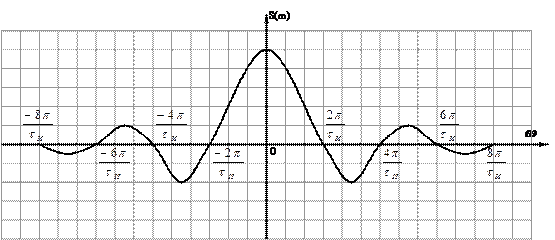 Изобразим спектральную плотность импульса на графике:
Изобразим спектральную плотность импульса на графике: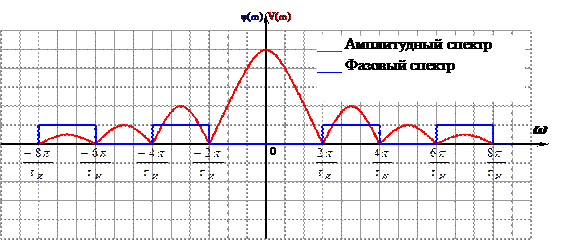
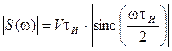 .
.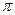 , то фазовый спектр описывается так:
, то фазовый спектр описывается так: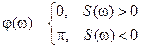 .
.
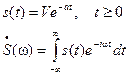 .
.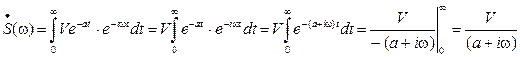 .
.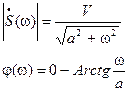 .
.
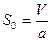 - площадь экспоненты.
- площадь экспоненты.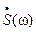 для следующей ситуации:
для следующей ситуации: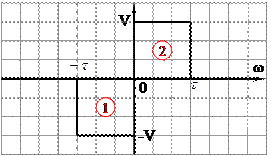
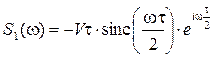 ,
,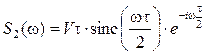 .
.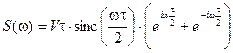 ,
,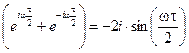 ,
,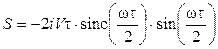 .
.
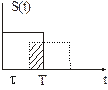
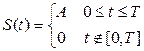 . Для
. Для 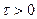 ,
, 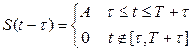 .
.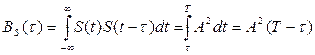
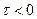 можно использовать четность
можно использовать четность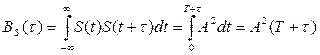
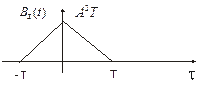
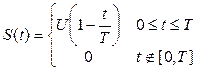 .
. 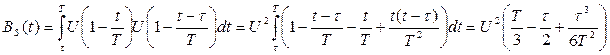
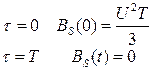 .
.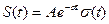 .
.