
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы логики высказываний - это формулы, принимающие значение «истина» при всех наборах значений своих пропозициональных переменных.Содержание книги
Поиск на нашем сайте
Такие всегда истинные выражения называют иногда еще и общезначимыми. Помимо того, что они позволяют исследовать мысль, не обращаясь к ее содержанию, сверх этого они еще и помогают совершать логические операции. Их можно в некоторых случаях исключать из выражений или, наоборот, вставлять в них, не внося при этом искажений в содержание заложенной в формулу мысли. Особенно часто приходится использовать такой прием при работе с нормальными формами. С помощью тождественно-истинных выражений легко записать и законы традиционной логики. Так, в формуле
нетрудно узнать закон запрета противоречия, а в формуле
- закон исключенного третьего. В самом деле, заменив в первой из них буквенную переменную на предложение «Гриб ядовитый», мы получим из данной формулы правильное высказывание: «Неверно, что гриб ядовитый и неядовитый». Проделав то же самое со второй, мы получим другое истинное высказывание: «Гриб либо ядовитый, либо неядовитый». На данной стадии мы в состоянии дать обоснование данным законам, опираясь на изложенные ранее принципы и правила. Формула для закона противоречия преобразуется в выражение, не содержащее отрицания над скобкой, если провести ряд эквивалентных замен, используя правила (1) и (2):
Легко видеть, что в данной дизъюнкции при любом значении переменной будет содержаться 1, а этого достаточно для того, чтобы дизъюнкция оказалась истинной (см. также раздел об элементарных дизъюнкциях). Общезначимость формулы для закона исключенного третьего непосредственно вытекает из полученной нами ранее формулы:
Применяя ее к выражению
Следовательно, и это выражение является истинным при любом значении переменной. Формулы символической логики второй разновидности из приведенных в таблице являются тождественно-ложными, поскольку всегда принимают значение «ложь». В этом смысле они противоположны формулам-законам. Правильнее всего поэтому называть такие выражения противоречиями. Противоречия - это формулы логики высказываний, принимающие значения «ложь» при любом наборе своих пропозициональных переменных. Не надо, однако, смотреть на формулы-противоречия как на какую-то досадную помеху в логике высказываний. Во-первых, превращение их в законы осуществляется простым отрицанием (это отличает противоречия символической логики от противоречий в логике традиционной). Так, закон противоречия представляет собой простое отрицание тождественно-ложного выражения Последняя категория выражений символической логики имеет в наборе своих значений как «истину», так и «ложь». Такой является третья из приведенных нами формул. Выражения данной разновидности называют нейтральными.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.234 (0.01 с.) |

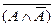
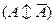
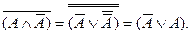
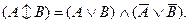
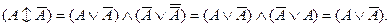
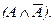 Во-вторых, постоянство семантического значения, даже ложного, все равно дает основу для анализа высказывания, записанного с помощью тождественно-ложной формулы. В-третьих, они, так же как и тождественно-истинные выражения, помогают осуществлять логические преобразования, упрощать когда надо сложные формулы.
Во-вторых, постоянство семантического значения, даже ложного, все равно дает основу для анализа высказывания, записанного с помощью тождественно-ложной формулы. В-третьих, они, так же как и тождественно-истинные выражения, помогают осуществлять логические преобразования, упрощать когда надо сложные формулы.


