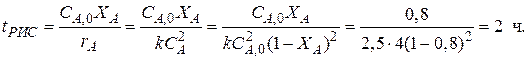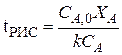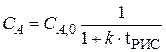Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проточный реактор идеального смешения в стационарном режимеСодержание книги
Поиск на нашем сайте
Условие его идеальности состоит в отсутствии градиента концентраций и температуры по объему, причем в стационарных условиях этот градиент отсутствует и во времени. При введении исходной смеси в большой реакционный объем происходит скачкообразное снижение концентрации концентраций реагентов до величины, равной концентрации в реакторе и на выходе. Таким образом, в реакторе идеального смешения реализуются, так называемые, безградиентные условия. В качестве элементарного объема для реактора идеального смешения можно принять полный объем реактора V. При стационарном режиме работы реактора не происходит изменения постоянных по объему концентраций элементов реакции и во времени, следовательно, в качестве элементарного промежутка времени можно принять любой конечный временной интервал, например единицу времени (1 с, 1 мин или 1 ч). Количество вещества А, которое за единицу времени войдет в реактор с конвективным потоком, будет равно FA ,0 = W 0 CA ,0,где W 0 – объемный расход реакционного потока на входе в аппарат. За это же время выйдет из реактора с конвективным потоком количество вещества A FA = WCA,а расход вещества A (или его образование) в ходе химической реакции составит rA V. При этом скорость rA определяется концентрацией CA. Стационарность процесса в проточном реакторе можно обеспечить, если объемные расходы на входе и выходе равны между собой (W 0 = W). Тогда
Величина Для гетерогенно-каталитических процессов:
Действительное время пребывания частиц в проточном реакторе смешения является случайной величиной в отличие от времени пребывания реагентов в периодическом реакторе. Пусть, например, в реактор введено N одинаковых частиц. В периодическом реакторе все они будут находиться равное время от загрузки до выгрузки. В проточном реакторе идеального смешения эти частицы мгновенно и равномерно распределяются по всему объему аппарата, и так как из аппарата непрерывно выходит поток продуктов, то в момент ввода частиц в реактор какое-то их количество может сразу же оказаться в выходном потоке. Некоторые частицы, равномерно распределяясь в новых порциях реакционной смеси, вошедшей в аппарат, могут находиться в нем бесконечно долго. Отсюда можно сделать вывод, что действительное время пребывания частиц в проточном реакторе – это случайная величина, которая может изменяться от 0 до ∞. Непрерывную случайную величину можно задать с помощью вероятностных характеристик, в частности функций распределения случайной величины. Использование в качестве характеристики времени пребывания частиц в проточном реакторе величины t является удобным способом усреднения действительного времени пребывания, так как эта величина связана с конструктивными характеристиками реактора: его объемом и объемным расходом реакционной смеси. Для решения практических задач удобно концентрацию реагента выразить через его степень превращения.
Уравнения материального баланса для проточного реактора идеального смешения в стационарном режиме имеют ряд отличий от соответствующих уравнений для периодического реактора. Следует отметить, что балансовые уравнения стационарного реактора идеального смешения записываются сразу в виде конечного алгебраического уравнения в отличие от дифференциальной формы исходных уравнений для периодического реактора. В уравнение для периодического реактора скорость rA следует подставлять в виде функциональной зависимости от концентрации rA (CA) или степени превращения rA (XA) и лишь после интегрирования уравнения возможна подстановка числовых значений. Этот факт, как и дифференциальная форма уравнений материального баланса, отражает зависимость параметров процесса в периодическом реакторе от времени. В стационарном режиме в любой точке реактора идеального смешения в любой момент времени концентрация постоянна. Следовательно, скорость реакции характеризуется каким-то одним конкретным числовым значением, определяемым этой концентрацией. Это число может быть сразу поставлено в уравнение материального баланса.
Пример. Рассчитать среднее время пребывания реагентов в проточном реакторе идеального смешения, необходимое для достижения степени превращения исходного реагента X А = 0,8. В реакторе протекает реакция второго порядка 2 А Решение. Для определения
Таким образом, для достижения степени превращения X А = 0,8 необходимо, чтобы соотношение между объемом реактора и объемным расходом через него Уравнения материального баланса для проточного реактора могут быть использованы не только для определения среднего времени пребывания Решение этой задачи не вызывает никаких затруднений, если скорость реакции описывается сравнительно простыми кинетическими уравнениями (уравнениями первого и второго порядка). Например, для реакции первого порядка А
получим Зачастую скорость сложных реакций с невыясненным до конца механизмом выражают в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным и приходится прибегать к численным методам расчета.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 713; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.196.141 (0.01 с.) |

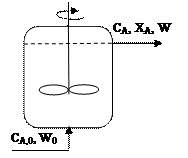 Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме.
Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме.
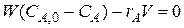 (1)
(1)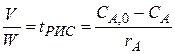 (2)
(2)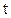 = V/ W в уравнении измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержимое проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе.
= V/ W в уравнении измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержимое проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе.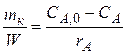 (3)
(3)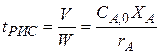 (4)
(4)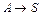
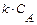
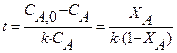
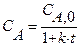
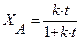
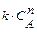 при
при 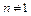
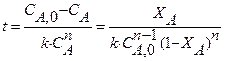
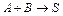
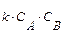
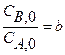
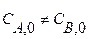
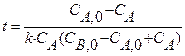
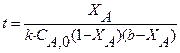
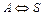
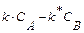
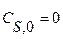
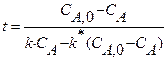
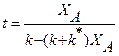
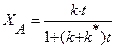
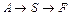
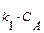
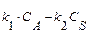
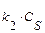
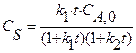
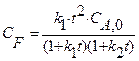
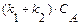
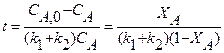
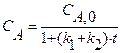
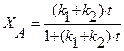
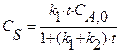
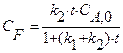
 R + S, скорость которой описывается при постоянной температуре кинетическим уравнением wrA = 2,5
R + S, скорость которой описывается при постоянной температуре кинетическим уравнением wrA = 2,5 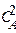 . Начальная концентрация реагента А на входе в реактор C А ,0 = 4 кмоль/м3.
. Начальная концентрация реагента А на входе в реактор C А ,0 = 4 кмоль/м3.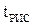 можно использовать уравнение (4) концентрацию реагента в реакторе, необходимую для расчета скорости протекающей в нем реакции, выразим через степень превращения
можно использовать уравнение (4) концентрацию реагента в реакторе, необходимую для расчета скорости протекающей в нем реакции, выразим через степень превращения