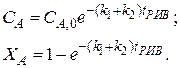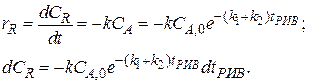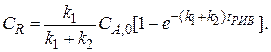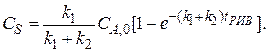Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реактор идеального вытесненияСодержание книги
Поиск на нашем сайте
Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме. Каждый элемент потока, условно выделенный двумя плоскостями, перпендикулярными оси канала, движется через него как твердый поршень, вытесняя предыдущие элементы потока и не перемешиваясь ни с предыдущими, ни со следующими за ним элементами. Реактор идеального вытеснения идеализированной моделью непрерывнодействующих аппаратов вытеснения, в которых реакционная масса движется вдоль оси, вытесняя последующие слои. Условие его идеальности состоит в том, что каждый элемент потока в данном поперечном сечении аппарата движется вдоль оси с одинаковой линейной скоростью (поршневой режим). Это предполагает отсутствие торможения стенками или насадкой, а также отсутствие диффузионных явлений. При стационарном режиме, т.е. при постоянстве скорости подачи и состава исходной смеси, а также условий теплообмена, каждый элемент потока пребывает в таком реакторе в течение одинакового времени, а концентрации и температура в каждом поперечном сечении остаются постоянными. При этом в отличие от периодического реактора концентрации веществ изменяются не во времени, а по длине аппарата. Следует отметить, что строго эти допущения в реальных реакторах не выполняются. Из гидравлики известно, что даже в очень гладких каналах при движении потока, характеризующегося высокими числами Рейнольдса Re, у стенок канала существует так называемый пограничный вязкий подслой, в котором градиент линейной скорости очень велик. В реальном реакторе можно приблизиться к режиму идеального вытеснения, если реакционный поток – турбулентный и при этом длина канала существенно превышает его поперечный размер (например, для цилиндрических труб L/D > 20). В соответствии с принятыми допущениями общее уравнение материального баланса для элементарного объема проточного реактора можно упростить. Прежде всего, в качестве элементарного объема в этом случае можно рассматривать объем, вырезанный двумя параллельными плоскостями, находящимися друг от друга на бесконечно малом расстоянии dz и перпендикулярными оси канала z. Конвективный перенос происходит только в направлении оси z. Диффузионный перенос в реакторе идеального вытеснения отсутствует (как и в реакторе смешения). Следовательно, уравнение материального баланса для реактора идеального вытеснения в нестационарном режиме работы примет вид
Из уравнения (1) видно, что в нестационарном реакторе идеального вытеснения концентрация реагента реакции является функцией двух переменных: координаты z и времени t. При стационарном режиме уравнение будет еще более простым (в этом случае концентрация является только функцией координаты z):
В реакторе с постоянной площадью поперечного сечения канала линейная скорость потока u z будет величиной постоянной, равной отношению объемного расхода W к площади сечения F (u z= W /F). Тогда, с учетом того, что Fz/ W = V/ W =
Следует еще раз обратить внимание на то, что величина Говоря о среднем времени пребывания Уравнение (3) для стационарного режима реактора идеального вытеснения можно проинтегрировать относительно
или, если A – исходный реагент,
Уравнения (4), (5) по виду напоминают характеристические уравнения для периодического реактора идеального смешения. Если считать, что элементарный объем dV,для которого составлялся материальный баланс, может двигаться вместе с потоком, в поршневом режиме он может рассматриваться как своеобразный периодический микрореактор идеального смешения, время проведения реакции в котором равно среднему времени пребывания реагентов в реакторе идеального вытеснения. Уравнения (4) и (5) могут быть использованы для расчета размеров изотермического реактора идеального вытеснения и глубины протекающего в нем процесса.
Пример. Определить среднее время пребывания реагентов в проточном реакторе идеального вытеснения (реакция второго порядка 2 А Решение. Используем для расчета уравнение:
Таким образом, для достижения аналогичных результатов значения Пример. Уравнения материального баланса могут быть использованы не только для определения среднего времени пребывания Приведем примеры аналитического решения математической модели для некоторых частных случаев. Простая элементарная реакция А
и интегрируем Тогда и Обратимая реакция А
Интеграл может быть записан в таком виде:
Из последнего выражения
или откуда
Параллельная реакция
Выражение скорости по компоненту R
Интегрируя левую часть равенства в пределах от C R ,0 до C R и правую – от нуля до
Аналогично находим
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |


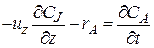 (1)
(1)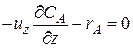 (2)
(2)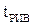 , уравнение (2)можно записать в таком виде:
, уравнение (2)можно записать в таком виде: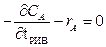 (3)
(3)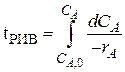 (4)
(4)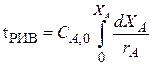 (5)
(5)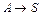
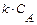
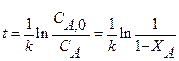
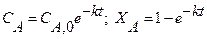
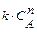 при
при 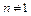
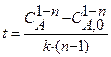
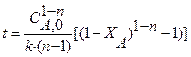
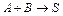
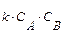
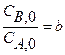
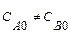
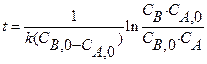
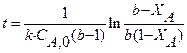
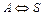
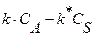
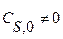
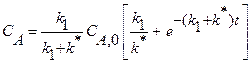
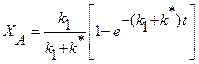
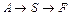
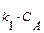
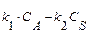
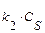
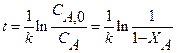
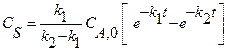
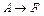
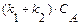
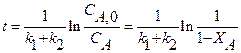
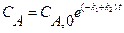
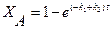
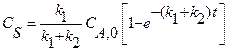
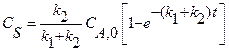
 R + S, кинетическое уравнение r A = 2,5 СА 2, C А, 0 = 4 кмоль/м3, X А = 0,8).
R + S, кинетическое уравнение r A = 2,5 СА 2, C А, 0 = 4 кмоль/м3, X А = 0,8).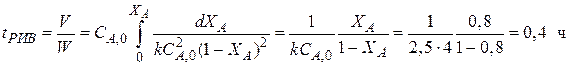
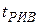 для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение
для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение 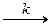 R. Скорость такой реакции r A = k C A C B. Подставляем это кинетическое уравнение в уравнение материального баланса
R. Скорость такой реакции r A = k C A C B. Подставляем это кинетическое уравнение в уравнение материального баланса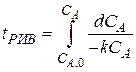
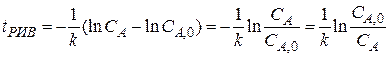

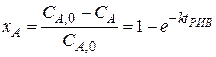
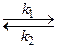 R. При условии, что C R ,0 = 0,
R. При условии, что C R ,0 = 0,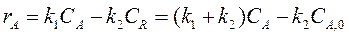
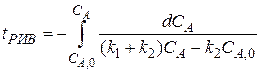
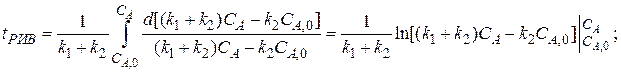
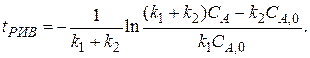
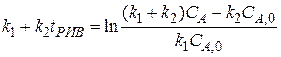



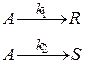 . Для этой реакции скорость по компоненту A r A = (k 1 + k 2) C A и выражения для C А и X А будут:
. Для этой реакции скорость по компоненту A r A = (k 1 + k 2) C A и выражения для C А и X А будут: