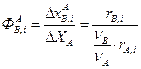Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каскад реакторов идеального смешения
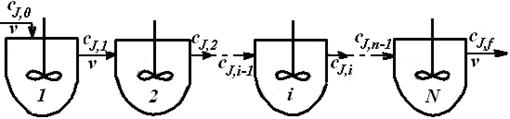
Каскад представляет собой несколько последовательно соединенных проточных реакторов (секций) идеального смешения (рис. 1). Реакционная смесь проходит через все секции. Можно рассматривать в качестве примера такой модели не только систему последовательно расположенных отдельных аппаратов, но и проточный реактор, тем или иным образом разделенный внутри на секции, в каждой из которых осуществляется перемешивание реакционной смеси.
Рис. 1. Схема каскада реакторов идеального смешения
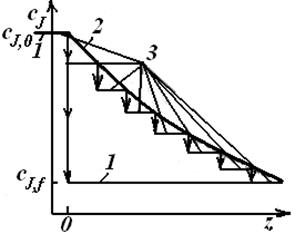
Для каскада реакторов идеального смешения должны выполняться следующие допущения об идеальности: 1. В каждой секции каскада выполняются условия реактора идеального смешения, т. е. мгновенное изменение параметров процесса, равенство параметров во всех точках секции и в потоке, выходящем из нее. 2. Отсутствие обратного влияния: каждый последующий реактор не влияет на предыдущий. На рис. 2 сравнивается характер изменения концентрации исходного реагента при прохождении реакционной смеси через различные реакторы.
Рис. 2. Изменение концентрации реагента при прохождении реакционной смеси через последовательные секции единичного реактора идеального смешения (1), реактора идеального вытеснения (2) и каскада реакторов идеального смешения (3) Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому-либо участнику реакции, включающую, по меньшей мере, N уравнений по числу секций каскада. Уравнения материального баланса для любой секции каскада однотипны. Материальный баланс по компоненту А для i -й секции в стационарном режиме работы каскада имеет вид: где Расчет каскада реакторов идеального смешения обычно сводится к определению числа секций заданного объема, необходимых для достижения определенной глубины превращения, или к определению состава реакционной смеси на выходе из i -й секции каскада.
Допущения об отсутствии обратного влияния в каскаде реакторов идеального смешения существенно упрощают расчет. Он сводится к последовательному решению уравнений материального баланса для каждой секции относительно концентрации реагента (или продукта) на выходе. Выходной параметр для первой секции (концентрация CA , i), полученный из первого уравнения, является входным параметром для второй секции, выходной параметр второй секции – входным для третьей и т. д. Различают аналитический метод и численные методы расчета каскада. Применение аналитического метода возможно в том случае, если уравнения материального баланса могут быть аналитически решены относительно концентрации CA. Это можно сделать, например, если протекающие реакции описываются кинетическими уравнениями первого или второго порядка. Рассмотрим определение концентрации реагента А на выходе из каскада реакторов, включающего в себя N секций равного объема (V 1 = V 2 =... = Vi...= VN)при проведении реакции первого порядка, скорость которой описывается уравнением r A = k C А. Из уравнения материального баланса для первой секции
определяем
Полученное значение C А ,1 подставляем в качестве входной концентрации в уравнение материального баланса для второй секции:
из него определяем
При равенстве объемов секций
Продолжая аналогичные расчеты, для последней секции каскада (N – число секций), получим
Если учесть, что
и тогда можно рассчитать число секций заданного объема, необходимых для достижения степени превращения X А: Если полученное при расчете по уравнению (4) N является дробным числом, его округляют в большую сторону. Уравнение (4)справедливо, естественно, только для реакции первого порядка. Для реакций, описываемых кинетическими уравнениями, не позволяющими аналитически решить уравнение (2)относительно C (например, реакции дробного порядка), при расчете каскада приходится прибегать к численным методам. Так как уравнения материального баланса для всех реакций однотипны, можно составить алгоритм решения этих уравнений для i -й секции и последовательно применить его N paз.
Наглядным является графический способ расчета каскада реакторов, использующий описанный выше графический метод определения концентрации реагентов на выходе из реактора идеального смешения. Принцип расчета остается прежним. Сначала, графически решая уравнение для первой секции
находят концентрацию C А ,1 (рис.3), построив кинетическую кривую r A и прямую с тангенсом угла наклона (–1/
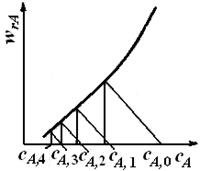
Для расчета концентрации на выходе из N -го реактора графическое решение повторяют N раз. Если требуется рассчитать число секций N,необходимое для достижения заданной степени превращения X А, графическое построение продолжают до тех пор, пока абсцисса точки пересечения прямой
и кривой r A не будет удовлетворять условию C А , i ≤ C А ,0(1 – хА).
Рис. 5.12. Зависимости скорости реакции от концентрации для расчета каскада реакторов идеального смешения, состоящего из секций одинакового объема.
В каскаде реакторов полного смешения:
где ΔXА – изменение степени превращения в i -аппарате; Ф B ,i A – селективность вещества В по реагенту А в i -аппарате:
1. В проточном реакторе идеального смешения проводится жидкофазная реакция первого порядка с константой скорости k = 0.25 мин-1 и достигается степень превращения, равная 0.6. Определить степень превращения, если вместо одного реактора взять три последовательно работающих реактора идеального смешения при том же реакционном объеме (Ответ: 0.936). 2. Определить число секций каскада реакторов идеального смешения при проведении реакции А → B+C, если k = 3 ч-1, степень превращения реагента А составляет 90 %, а время пребывания в одной секции – 0.5 ч (Ответ: 3).
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.22.169 (0.011 с.) |
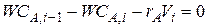 (1)
(1)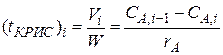 (2)
(2)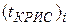 – среднее время пребывания реакционной смеси в i -й секции;
– среднее время пребывания реакционной смеси в i -й секции; 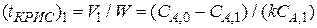
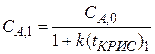
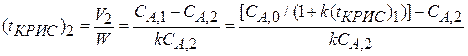
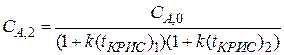
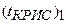 =
= 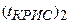 =...=
=...= 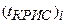 =... =
=... = 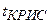
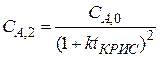
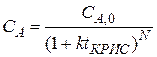 (3)
(3)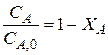 ,уравнение (3)можно записать в виде
,уравнение (3)можно записать в виде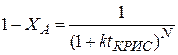
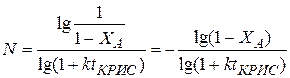 (4)
(4)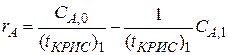
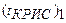 ), пересекающую ось абсцисс в точке C А ,0. Определив C А ,1, решают уравнение для второй секции:
), пересекающую ось абсцисс в точке C А ,0. Определив C А ,1, решают уравнение для второй секции: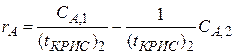
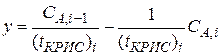
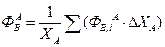 ,
,