Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 34. Конструктивный расчет ленточного вакуум-фильтра.Содержание книги
Поиск на нашем сайте Составить материальный баланс процесса фильтрования, а также определить основные конструктивные параметры фильтровальной перегородки при разделении суспензии в количестве 60,2 т/ч и рабочем давлении 5∙104 Па. Удельное объемное сопротивление осадка 4∙109 м-2, сопротивление фильтровальной перегородки 4,1∙109 м-1. Толщина осадка в зоне фильтрования 8 мм. Вязкость жидкой фазы суспензии 0,9∙10-3 Па∙с. Плотность твердой фазы суспензии 2000 кг/м3, жидкой фазы –1000 кг/м3. Соотношение твердой и жидкой фаз в исходной суспензии равно 1,2. Содержание влаги в мокром осадке после процесса фильтрования не должно превышать 6%.
Решение: Уравнение материального баланса процесса фильтрования, согласно закону сохранения массы, в общем виде можно представить как G сусп = G ос + G фил Уравнение материального баланса процесса фильтрования по твердой (распределенной) фазе можно представить в виде G сусп ∙ х сусп = G ос ∙ х ос + G фил ∙ х фил, где G сусп, G ос, G фил – расходы исходной суспензии, мокрого осадка, фильтрата, соответственно. х сусп, х ос, х фил – концентрация твердой фазы в исходной суспензии, мокрого осадка, фильтрата, соответственно. Согласно исходным данным соотношение твердой и жидкой фаз в исходной суспензии равно 1,2, следовательно, концентрацию твердой фазы в исходной суспензии можно определить по уравнению
где G тв, G ж – количество твердой и жидкой фаз в исходной суспензии, соответственно. 1,2∙ G тв = G ж
Согласно исходным данным содержание влаги в мокром осадке не должно превышать 6%, т.е. в мокром осадке находится жидкой фазы в объеме 6% от общей смеси и твердой фазы в объеме 94% от общей смеси. Тогда концентрация твердой фазы в мокром осадке составит
где G ’ тв, G ’ ж – количество твердой и жидкой фаз в мокром осадке
Считаем, что процесс фильтрования прошел эффективно и в фильтрате твердая фаза отсутствует, т.е. х фил = 0. Подставляем в уравнение материального баланса по твердой (распределенной) фазе процесса фильтрования все известные величины и определяем количество образовавшегося мокрого осадка 60,2∙ 0,45 = Gос ∙ 0,94 + Gфил ∙ 0, Gос = 60,2∙ 0,45/0,94 = 28,8 т/ч Из уравнения материального баланса процесса фильтрования в общем виде определяем количество фильтрата G фил = G сусп – G ос =60,2 – 28,8 = 31,4 кг/ч Таблица 7 Материальный баланс процесса фильтрования
Определим удельную производительность фильтра, по уравнению
где h ос – толщина слоя осадка на фильтрующей перегородке, hос = 0,008 м. U – соотношение объемов мокрого осадка и фильтрата, получающихся в процессе фильтрования.
где V ос, V фил – объемные расходы мокрого осадка и фильтрата, получающиеся в процессе фильтрования, соответственно.
В процессе фильтрования всю рабочую поверхность ленточного вакуум-фильтра условно можно разделить на три части: – зона фильтрования, – зона уплотнения (промывка), – зона просушки. Следовательно, конструкция фильтра, а именно длина рабочей части фильтровальной перегородки должна обеспечивать полное осуществление стадий процесса. Определим время нахождения мокрого осадка в зоне фильтрования
где V сусп – объемный расход суспензии, V сусп = V ос + V фил. b 1 – коэффициент, зависящий от свойств твердого материала,
где µ – вязкость жидкой фазы суспензии, µ = 0,9∙10-3 Па∙с; r 0 – удельное объемное сопротивление осадка, r 0 = 4∙109 м-2; P – рабочее давление, P = 5∙104 Па; с – поправочный коэффициент;
V сусп = V ос + V фил = 0,004 + 0,00865 = 0,01265 м3/ч
Определим время нахождения мокрого осадка зоне уплотнения (промывки)
где b 2 – коэффициент, зависящий от свойств твердого материала,
где α0 – необходимое количество промывной жидкости на 1 кг мокрого осадка α0 = 0,0005 м3/кг. P пр – давление при котором подается промывная жидкость, P пр=105 Па; ρос – плотность мокрого осадка
Определим время нахождения мокрого осадка зоне просушки исходя из условий, что оно составляет 50% от времени фильтрования
Общее время рабочего цикла процесса фильтрования
Общую скорость процесса фильтрования определяется по уравнению
Определяем необходимую площадь фильтрования
где
Из конструктивных соображений принимаем рабочую ширину фильтрующей перегородки b =1,2 м, тогда длина рабочей части фильтрующей перегородки составит Задания для самоконтроля I тип задач
1. Определить полное гидростатическое давление на дно сосуда, наполненного жидкостью. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина жидкости в сосуде h. Температура жидкости t.
2. Определить манометрическое давление на дно сосуда, наполненного жидкостью. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина жидкости в сосуде h. Температура жидкости t.
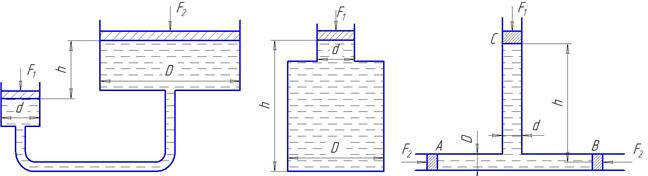
3. Какую силу F 2 (рис.18) нужно приложить к большему поршню, чтобы система находилась в равновесии. Сила, приложенная к меньшему поршню F 1. Диаметр большего поршня D, меньшего d. Разность уровней h. Трубки заполнены жидкостью. Весом поршней пренебречь. Температура жидкости t.
4. Определить силу манометрического давления на дно сосуда (рис.19), если сила, действующая на поршень равна F 1. Диаметр d, глубина жидкости в сосуде h, диаметр дна сосуда D. Температура жидкости t.
5. Труба диаметром D соединена с трубой диаметром d (рис.20). Высота столба жидкости h. В трубах имеются поршни. Какое усилие F 2 нужно приложить на поршни А и В, чтобы система находилась в равновесии, если на поршень С действует сила F 1. Температура жидкости t.
Рис. 18 Рис.19 Рис. 20 Таблица 8
II тип задач
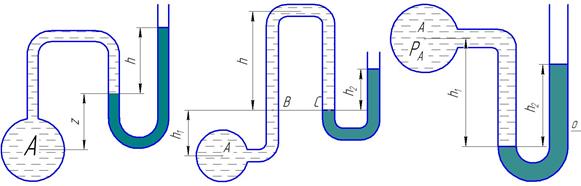
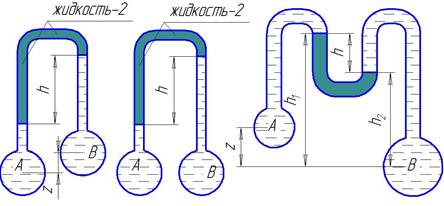
1. Определить на какой высоте z установится уровень ртути в пьезометре (рис. 21), если при манометрическом давлении в трубе Р А и показании h система находится в равновесии. Температура жидкостей t.
2. Определить манометрическое давление в точке А трубопровода (рис. 22), если высота столба ртути по пьезометру h 2. Центр трубопровода расположен на h 1 ниже линии раздела между жидкостью и ртутью. Температура жидкостей t.
3. Определить манометрическое и абсолютное давление в баллоне А (рис. 23), если в баллоне и в левой трубке – жидкость, а в правой – ртуть. Высоты равны h 1 и h 2. Температура жидкостей t.
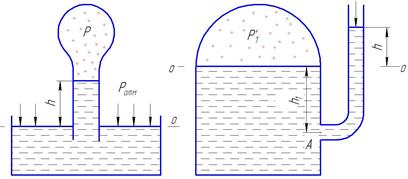
4. Определить высоту, на которую поднимается жидкость в вакуумметре (рис. 24), если абсолютное давление воздуха внутри баллона Р. Температура жидкостей t.
5. Определить высоту столба воды в пьезометре над уровнем жидкости в закрытом сосуде (рис. 25). Жидкость в сосуде находится под абсолютным давлением P 1. Температура жидкостей t.
Рис. 21 Рис. 22 Рис. 23
Рис. 24 Рис. 25 Таблица 9
III тип задач
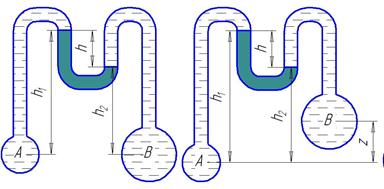
1. Определить при помощи дифференциального манометра разность давлений в точках В и А двух трубопроводов, заполненных жидкостью 1 (рис 26). Высота столба жидкости 2 h. 2. Определить высоту столба жидкости 1 h, при разности манометрических давлений в точках В и А двух трубопроводов, заполненных жидкостью 2, D Р (рис 27). Перепад высот между центрами трубопроводов z.
3. Определить высоту столба жидкости 2 h, при разности манометрических давлений в точках В и А двух трубопроводов, заполненных жидкостью 1 (рис. 28).
Рис. 26 Рис. 27 4. Для схемы показанной на рис. 29, превышение точки В над точкой А равно z. В качестве рабочей жидкости применена жидкость 2. Определить разность давлений в баллонах при показании прибора h, если в баллонах жидкость 1.
Рис.28 Рис.29 Рис. 30 5. Для схемы показанной на рис. 30, превышение точки В над точкой А равно z. Разность давлений в баллонах D Р. Баллоны наполнены жидкостью 1. В качестве рабочей жидкости применена жидкость 2. Определить показания пьезометра h Таблица 10
IV тип задач 1. Определить расход жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, который сможет перемещаться по стальному трубопроводу длиной 150 м, диаметром 100 мм, с шероховатостью стенок 0,05 мм при помощи насоса с потребным напором 50 м. Точка забора находится над точкой потребления на высоте 3 метра. При решении задачи не учитывать влияние температуры на свойства жидкости.
2. Определить потребный напор, который необходимо создать насосу для перемещения 65л/с жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, по стальному трубопроводу, состоящего из двух частей длиной 100 м и 500 м соответственно. Шероховатость стенок первого участка трубопровода с диаметром 100 мм составляет 0,05 мм, шероховатость стенок второго участка трубопровода с диаметром 150 мм – 0,1 мм. Коэффициент местного сопротивления при внезапном расширении трубопровода, при переходе с одного диаметра на другой, равен 3. Жидкость со второго участка трубопровода под избыточным давлением 0,01 МПа распыляется в атмосфере через распределительное устройство. Коэффициент местного сопротивления распределительного устройства равен 5. При решении задачи не учитывать влияние температуры на свойства жидкости.
3. Определить оптимальный диаметр стального трубопровода, который может пропустить расход жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, равный 60 л/с. Длина трубопровода составляет 500 м, шероховатость стенок трубопровода 0,1 мм. Жидкость перемещается при помощи насоса с потребным напором 75 м. Точка забора находится под точкой потребления на высоте 5 метров. При решении задачи не учитывать влияние температуры на свойства жидкости.
4. Определить потери напора на трение со стенками трубопровода, которые возникают при перемещении 50л/с жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, по стальному трубопроводу, состоящего из двух частей длиной 100 м и 500 м соответственно. Шероховатость стенок первого участка трубопровода с диаметром 100 мм составляет 0,05 мм, шероховатость стенок второго участка трубопровода с диаметром 150 мм – 0,1 мм. Коэффициент местного сопротивления при внезапном расширении трубопровода, при переходе с одного диаметра на другой, равен 3. При решении задачи не учитывать влияние температуры на свойства жидкости.
5. Определить потери давления, которые возникают при перемещении 90л/с жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, по стальному трубопроводу длиной 250 м. Шероховатость стенок трубопровода диаметром 100 мм составляет 0,1 мм. При решении задачи не учитывать влияние температуры на свойства жидкости.
Приложение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

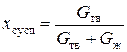 ,
,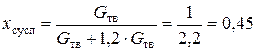 кг/кг
кг/кг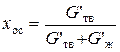 ,
,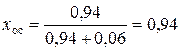 кг/кг
кг/кг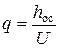 ,
,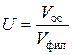 ,
,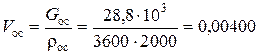 м3/с.
м3/с.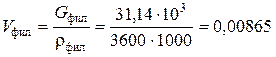 м3/с.
м3/с.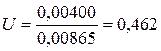
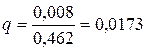 м
м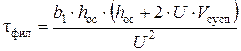 ,
,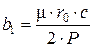
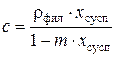
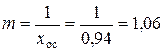
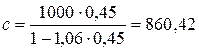
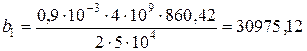
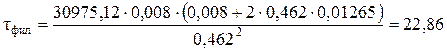 с.
с.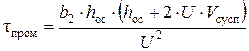
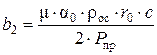
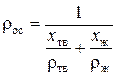
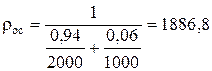 кг/м3.
кг/м3.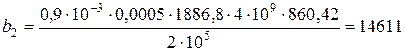
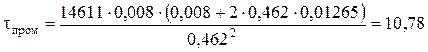 с
с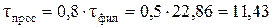 с.
с.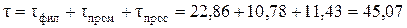 с.
с.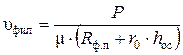
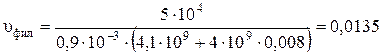 м/с
м/с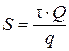
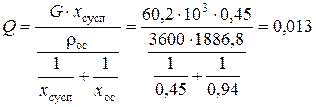
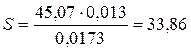 м2.
м2.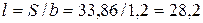 м.
м.