
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 20. Определение расхода жидкости.
Определить расход жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, который сможет перемещаться по стальному трубопроводу длиной 150 м, диаметром 100 мм, с шероховатостью стенок 0,05 мм при помощи насоса с потребным напором 50 м. Точка забора находится над точкой потребления на высоте 3 метра. При решении задачи не учитывать влияние температуры на свойства жидкости.
Решение: Выполним перевод внесистемных величин в систему СИ Δ=0,05×10-3 м.
Рассмотрим два сечения трубопровода. Первое сечение – начало трубопровода, второе – окончание трубопровода. Расход жидкости определяется из уравнения потребного напора, создаваемого насосом для перемещения жидкости Н потр.= Н ст + К × Qm, где Н ст – статический напор, К, m – коэффициенты, зависящие от режима движения жидкости. Н ст=(z 2 – z 1)+ P 2/ρ× g, где z 1, z 2 – координаты рассматриваемых сечение по оси ординат, относительно плоскости сравнения. Так как по условиям задачи указано, что точка забора находится над точкой потребления на высоте 3 метра, то (z 2 – z 1)=-3 м Р 2 – давление жидкости во втором сечении. Так как по условиям задачи не указана никакая информация о давлении, то давление Р 2 =0 Н ст= -3+0=-3 м. Согласно практическим данным, при значении коэффициента кинематической вязкости менее 0,1 Ст, режим движения жидкости в трубопроводе турбулентный, более 0,1 Ст режим движения жидкости – ламинарный. Определим кинематический коэффициент вязкости жидкости
Так как ν=0,0101 Ст < 0,1 Ст – режим движения жидкости турбулентный. При турбулентном режиме движении данный тип задач решается методом последовательных приближений. В первом приближении произвольным образом принимается значение коэффициента Дарси из диапазона значений 0,015÷0,025 и из уравнения потребного напора определяется величина расхода. Принимаем значение коэффициента Дарси λ1=0,020. Определяем значение коэффициента К в уравнении потребного напора
Определяем значение расхода в первом приближении Н потр.= Н ст + К × Qm. 50 = -3 + 24813× Q 2. Q 1 = 0,0462 м3/с. Выполняем проверку достоверности первого приближения. Определяем скорость движения жидкости в трубопроводе
Определяем режим движения жидкости в трубопроводе
Так как Re 1>2320, то режим движения жидкости в трубопроводе будет турбулентным. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 1 > Re г/гл, то определяем «границу» переходной области сопротивления
Так как Re кв > Re 1 > Re г/гл, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определяем значение коэффициента К в уравнении потребного напора (во втором приближении)
Определяем значение расхода в первом приближении Н потр.= Н ст + К × Qm 50 = -3 + 21463× Q 2. Q 2 = 0,0497 м3/с. Сравниваем значение расхода жидкости в первом и втором приближениях. Так как Q 1 = 0,0462 м3/с ≠ Q 2 = 0,0497 м3/с, первое приближение не достоверно, выполняем проверку достоверности второго приближения, с учетом того, что расход равен Q 2. Определяем скорость движения жидкости в трубопроводе
Определяем режим движения жидкости в трубопроводе
Так как Re 2>2320, то режим движения жидкости в трубопроводе будет турбулентным. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 2 > Re г/гл, то определяем «границу» переходной области сопротивления
Так как Re кв > Re 2 > Re г/гл, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определяем значение коэффициента К в уравнении потребного напора (во втором приближении)
Определяем значение расхода во третьем приближении Н потр.= Н ст + К × Qm 50 = -3 + 21339× Q 2. Q 2 = 0,0498 м3/с. Сравниваем значение расхода жидкости в втором и третьем приближениях. Так как Q 2 = 0,0497 м3/с ≈ Q 3 = 0,0498 м3/с (значение расходов во втором и третьем приближениях совпадают с точностью в третьем знаке после запятой), то второе приближение является достоверным. Принимаем в качестве окончательного значения расход равный Q = Ответ: расход жидкости равен Q = 0,0497 м3/с ≈ 49,7 л/с.
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.121.160 (0.014 с.) |
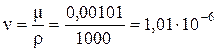 м2/с=0,0101×10-4 м2/с=0,0101 Ст.
м2/с=0,0101×10-4 м2/с=0,0101 Ст.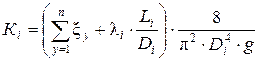 ,
,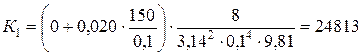 ,
,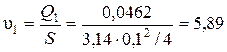 м/с.
м/с.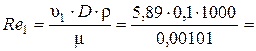 583168
583168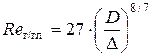
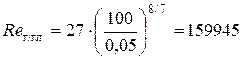
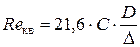
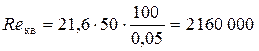
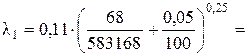 0,0173
0,0173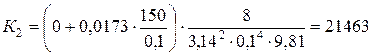 ,
,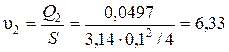 м/с.
м/с.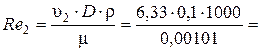 626733
626733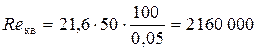
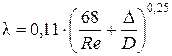
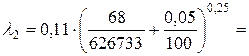 0,0172
0,0172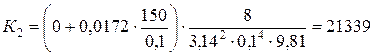 ,
,


