
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 22. Определение оптимального диаметра трубопровода.
Определить оптимальный диаметр стального трубопровода, который может пропустить расход жидкости плотностью 1000 кг/м3, вязкостью 0,00101 Па×с, равный 60 л/с. Длина трубопровода составляет 500 м, шероховатость стенок трубопровода 0,1 мм. Жидкость перемещается при помощи насоса с потребным напором 75 м. Точка забора находится под точкой потребления на высоте 5 метров. При решении задачи не учитывать влияние температуры на свойства жидкости.
Решение: Выполним перевод внесистемных величин в систему СИ: Q =60 л/с = 60×10-3 м3/с; Δ=0,1 мм = 0,1×10-3 м. Рассмотрим два сечения трубопровода. Первое сечение – начало трубопровода, второе – окончание трубопровода. Оптимальный диаметр определяется из уравнения потребного напора, создаваемого насосом для перемещения жидкости Н потр.= Н ст + К × Qm, где Н ст – статический напор; К, m – коэффициенты, зависящие от режима движения жидкости. Н ст=(z 2 – z 1)+ P 2/ρ× g, где z 1, z 2 – координаты рассматриваемых сечение по оси ординат, относительно плоскости сравнения. Так как по условиям задачи указано, что точка забора находится под точкой потребления на высоте 5 метра, то (z 2 – z 1)=5 м Р 2 – давление жидкости во втором сечении. Так как по условиям задачи не указана никакая информация о давлении, то давление Р 2 =0 Н ст= 5+0=5 м. Так как величина диаметра трубопровода является основным параметров трубопровода, и входит во все математические формулы, описывающие гидравлические характеристики трубопровода, то без величины диаметра трубопровода решить какую-либо задачу по гидравлике невозможно. Поэтому данная задача решается методом приближения. В первом приближении произвольным образом задаемся значением диаметра трубопровода D 1=100 мм = 0,1 м. Определим режим движения жидкости в трубопроводе. Для этого определим критерий Рейнольдса и сравним его с граничным значением критерия Рейнольдса.
Для определения критерия Рейнольдса Re1 необходимо определить скорость движения жидкости в трубопроводе при диаметре D 1= 0,1 м
Так как Re 1>2320, то режим движения жидкости в трубопроводе – турбулентный. При турбулентном режиме движения жидкости коэффициент m =2, коэффициент К определяется по формуле
где λi – коэффициент Дарси, для i-го участка. Коэффициент Дарси определяется в зависимости от режима движения жидкости и области сопротивления.
Так как режим движения жидкости в трубопроводе турбулентный, то необходимо определить область сопротивления. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 1 > Re г/гл1, то определяем «границу» переходной области сопротивления
Так как Re кв1 > Re 1 > Re г/гл1, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определим коэффициент К 1 для первого приближения
Определяем потребный напор, необходимый для перемещения жидкости по трубопроводу при диаметре трубопровода D 1 = 100 мм.
Значение Н потр1 = 302,8 м ≠ Н потр= 75 м, следовательно, первое предположение, что диаметр трубопровода равен D 1=100 мм неверно. Во втором приближении произвольным образом задаемся значением диаметра трубопровода D 1=150 мм = 0,15 м. Определим критерий Рейнольдса и сравним его с граничным значением критерия Рейнольдса.
Для определения критерия Рейнольдса Re 2 необходимо определить скорость движения жидкости в трубопроводе при диаметре D 2= 0,15 м
Так как Re 2>2320, то режим движения жидкости в трубопроводе – турбулентный. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 2 > Re г/гл2, то определяем «границу» переходной области сопротивления
Так как Re кв2 > Re 2 > Re г/гл2, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определим коэффициент К для второго приближения
Определяем потребный напор, необходимый для перемещения жидкости по трубопроводу при диаметре трубопровода D 1 = 150 мм.
Значение Н потр.2 = 42,1 м ≠ Н потр.= 75 м, следовательно, второе предположение, что диаметр трубопровода равен D 2=150 мм неверно. Сравнивая значения потребного напора в первом и втором приближениях, с исходным потребным напором, можно сделать вывод, что Н потр.2 < Н потр. < Н потр.1,
следовательно, искомый диаметр трубопровода должен находиться в интервале значений между D 1 и D 2, т.е. между 100 мм и 150 мм, причем значение искомого диаметра должно находиться ближе к диаметру D 2 Принимаем в третьем приближении диаметр трубопровода D 3=140мм=0,14 м. Определим критерий Рейнольдса и сравним его с граничным значением критерия Рейнольдса.
Для определения критерия Рейнольдса Re 3 необходимо определить скорость движения жидкости в трубопроводе при диаметре D 3= 0,14 м
Так как Re 3>2320, то режим движения жидкости в трубопроводе – турбулентный. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 3 > Re г/гл3, то определяем «границу» переходной области сопротивления
Так как Re кв 3 > Re 3 > Re г/гл3, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определим коэффициенты К для третьего приближения
Определяем потребный напор, необходимый для перемещения жидкости по трубопроводу при диаметре трубопровода D 3 = 140 мм.
Значение Н потр.3 = 57,6 м ≠ Н потр.= 75 м, следовательно, второе предположение, что диаметр трубопровода равен D 3=140 мм неверно. Сравнивая значения потребного напора в первом и третьем приближениях, с исходным потребным напором, можно сделать вывод, что Н потр.3 < Н потр. < Н потр.1, следовательно, искомый диаметр трубопровода должен находиться в интервале значений между D 1 и D 3, т.е. между 100 мм и 140 мм, причем значение искомого диаметра должно находиться ближе к диаметру D 3. Принимаем в четвертом приближении диаметр трубопровода Определим критерий Рейнольдса и сравним его с граничным значением критерия Рейнольдса
Для определения критерия Рейнольдса Re 4 необходимо определить скорость движения жидкости в трубопроводе при диаметре D 4= 0,13 м
Так как Re 4>2320, то режим движения жидкости в трубопроводе – турбулентный. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re 4 > Re г/гл4, то определяем «границу» переходной области сопротивления
Так как Re кв4 > Re > Re г/гл4, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определим коэффициент К для четвертого приближения
Определяем потребный напор, необходимый для перемещения жидкости по трубопроводу при диаметре трубопровода D 4 = 130 мм
Значение Н потр.4 = 81,2 м ≠ Н потр.= 75 м, следовательно, второе предположение, что диаметр трубопровода равен D 4=130 мм неверно. Сравнивая значения потребного напора в первом и третьем приближениях, с исходным потребным напором, можно сделать вывод, что Н потр.3 < Н потр. < Н потр.4, следовательно, искомый диаметр трубопровода должен находиться в интервале значений между D 3 и D 4, т.е. между 130 мм и 140 мм, причем значение искомого диаметра должно находиться ближе к диаметру D 4. По полученным данным в соответствующих масштабах строим зависимость между диаметром трубопровода и потребным напором Таблица1
По полученной зависимости при потребном напоре Н потр.= 75 м (см. исходные данные) оптимальный диаметр трубопровода составляет D ≈ 133 мм. В соответствии с ГОСТ 8732-78 «Трубы стальные бесшовные горячедеформированные. Сортамент» выбираем трубу Ø146х6,5 мм. Таким образом, диаметр условного прохода трубопровода составит 133 мм.
Определяем фактический потребный напор, необходимый для перемещения 60 л/с жидкости по трубопроводу диаметром 133 мм. Определим критерий Рейнольдса и сравним его граничным значением критерия Рейнольдса
Для определения критерия Рейнольдса Re4 необходимо определить скорость движения жидкости в трубопроводе при диаметре D = 0,133 м
Так как Re >2320, то режим движения жидкости в трубопроводе –турбулентный. Определяем «границу» области сопротивления гидравлически гладких труб
Так как Re > Re г/гл, то определяем «границу» переходной области сопротивления
Так как Re кв > Re > Re г/гл, то область сопротивления в трубопроводе будет переходной областью сопротивления. Для переходной области сопротивления коэффициент Дарси определяется по формуле
Определим коэффициент К
Определяем потребный напор, необходимый для перемещения жидкости по трубопроводу при диаметре трубопровода D = 133 мм
Так как Н потр=72,97 ≈ Н потр=75 мм, то диаметр трубопровода D = 133 мм является оптимальным. Ответ: оптимальным внутренним диаметром трубопровода является диаметр Ø133 мм.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.187.121 (0.036 с.) |
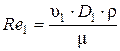
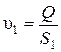
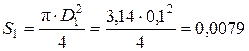 м2
м2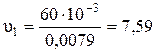 м/с,
м/с,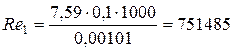
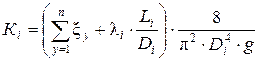 ,
,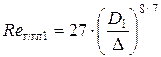
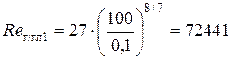
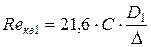
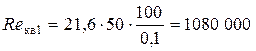
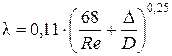
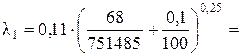 0,020
0,020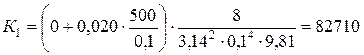 ,
,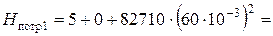 302,8 м
302,8 м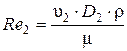
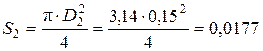 м2
м2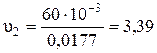 м/с,
м/с,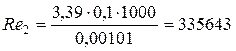
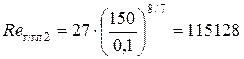
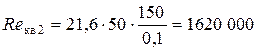
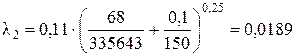
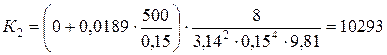 ,
,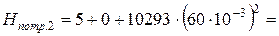 42,1 м.
42,1 м.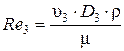
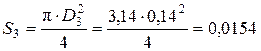 м2
м2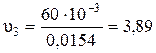 м/с,
м/с,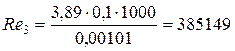
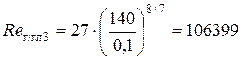
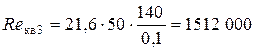
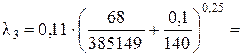 0,019
0,019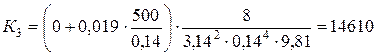 ,
,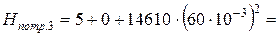 57,6 м
57,6 м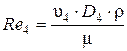 .
.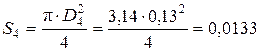 м2,
м2,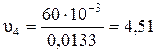 м/с,
м/с,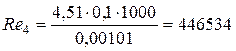 .
.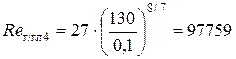
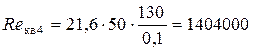
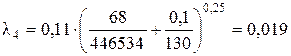
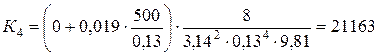 ,
,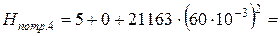 81,2 м
81,2 м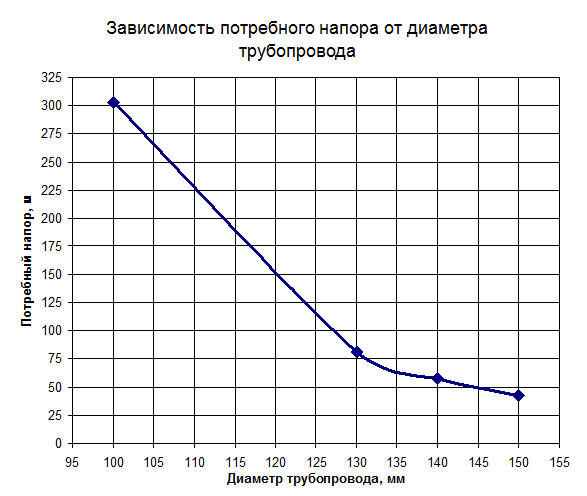
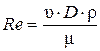 .
.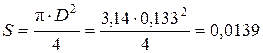 м2,
м2,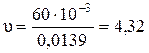 м/с,
м/с,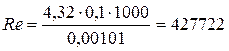 .
.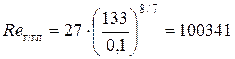
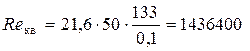
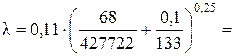 0,019
0,019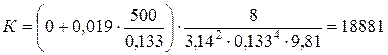 ,
,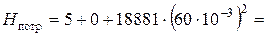 72,97 м.
72,97 м.


